絶対値のある関数のグラフと領域(神戸大2016文系第2問)

$a$ を正の定数とし，$f(x)=|x^2+2ax+a|$ とおく。以下の問に答えよ。

(1) $y=f(x)$ のグラフの概形をかけ。

(2) $y=f(x)$ のグラフが点 $(-1,2)$ を通るときの $a$ の値を求めよ。また，そのときの $y=f(x)$ のグラフと $x$ 軸で囲まれる図形の面積を求めよ。

(3) $a=2$ とする。すべての実数 $x$ に対して $f(x)\geqq2x+b$ が成り立つような実数 $b$ の取りうる値の範囲を求めよ。

負の値をとるとき・とらないとき

(1)から始めます。

絶対値があるので，絶対値の中が正の数になるときと負の数になるときで，分けて考えなければなりません。とは言え，それは $a$ の値によって変わります。

$x^2+2ax+a$ は下に凸のグラフなので，いったん平方完成して頂点が $x$ 軸より上になるか下になるかを考えましょう。

$y=x^2+2ax+a$ として
$=(x+a)^2-a^2+a$
$=(x+a)^2+a-a^2$

頂点は $(-a,a-a^2)$ となるので，$a-a^2\leqq0$ のとき，関数は負の値をとる部分ができ，$a-a^2>0$ ならば 0 または正の値をとることになります。
$a-a^2\leqq0$
$a^2\geqq a$

$a$ は正の数だから両辺を $a$ で割ることができます。

$a>1$

また

$a-a^2>0$
$a^2<a$
$a<1$

$a$ は正の数だから，$a\geqq1$ のときと，$0<a<1$ のときでグラフの形が変わります。

グラフの概形を 2 つに分けて描きましょう。

$a\geqq1$ のとき

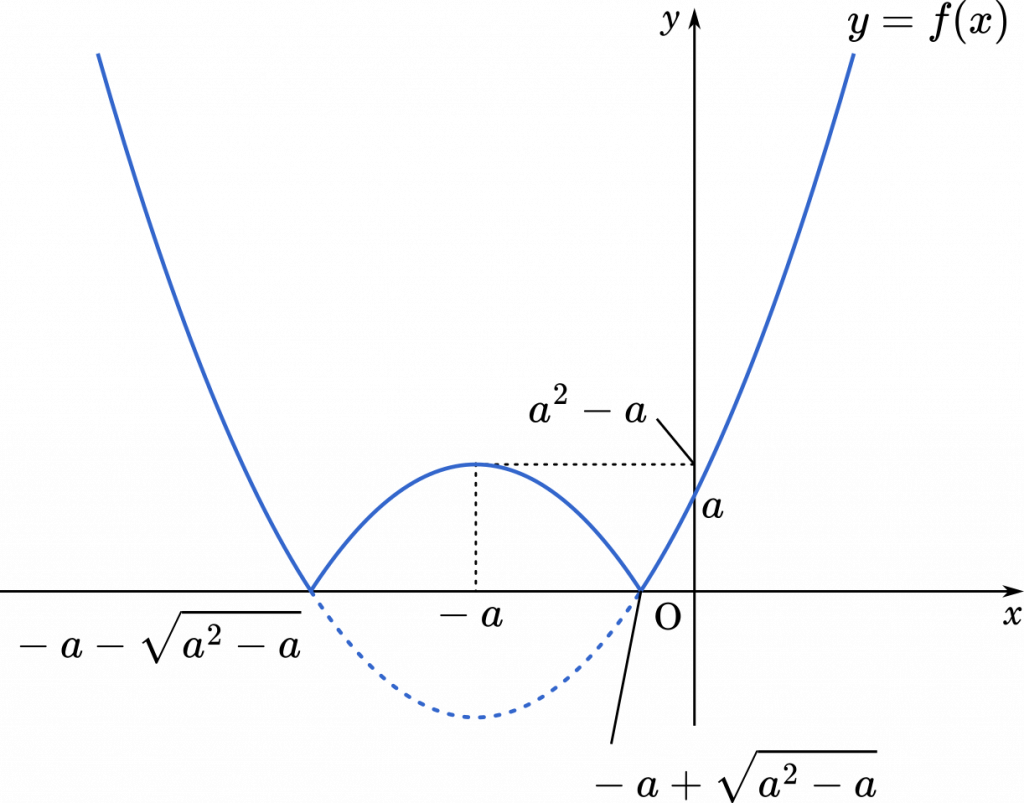
$0<a<1$ のとき

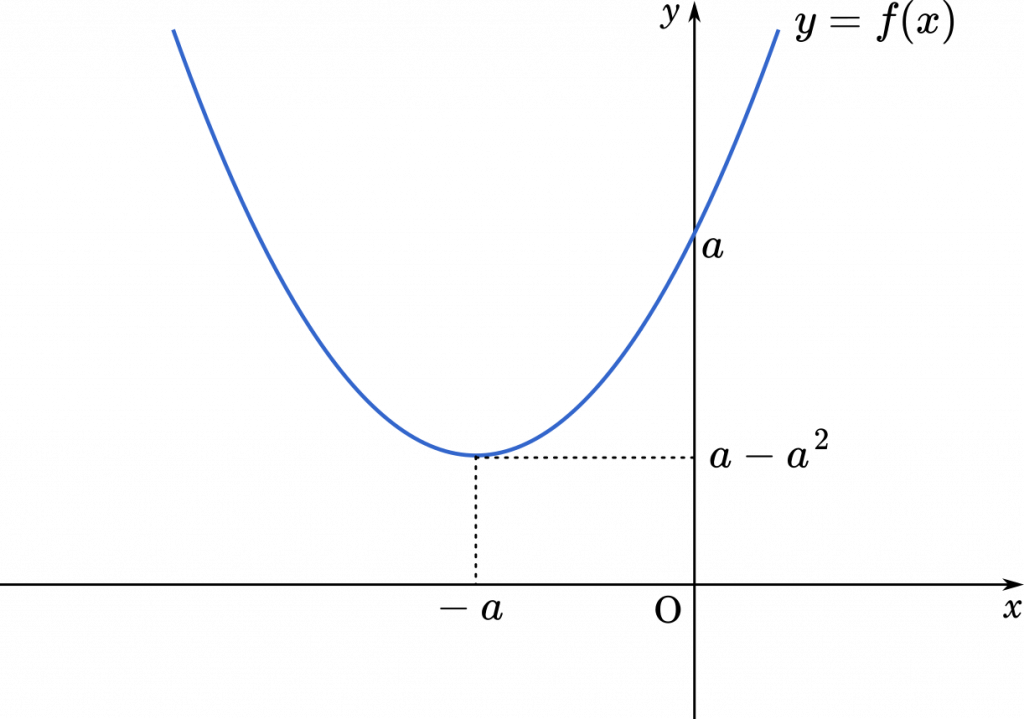
面積を求める

(2)に進みます。

$y=|x^2+2ax+a|$ に $(x,y)=(-1,2)$ を代入すると

$2=|(-1)^2+2a(-1)+a|$
$2=|1-2a+a|$
$2=|1-a|$

絶対値の部分を考えると，$a$ が 1 より小さければ $1-a$ は正の数で，1 より大きければ負の数になります。

$0<a<1$ のとき

$2=1-a$
$a=-1$　→$a$ は正の数だから，不適

$a\geqq1$ のとき

$2=-1+a$
$a=3$

よって，$a=3$　（答え）

次に，面積を求めます。

$f(x)$ に $a=3$ を代入すると

$f(x)=|x^2+6x+3|$
$=|(x+3)^2-9+3|$
$=|(x+3)^2-6|$

$(x+3)^2-6=0$ とすると
$(x+3)^2=6$
$x+3=\pm\sqrt{6}$
$=-3\pm\sqrt{6}$

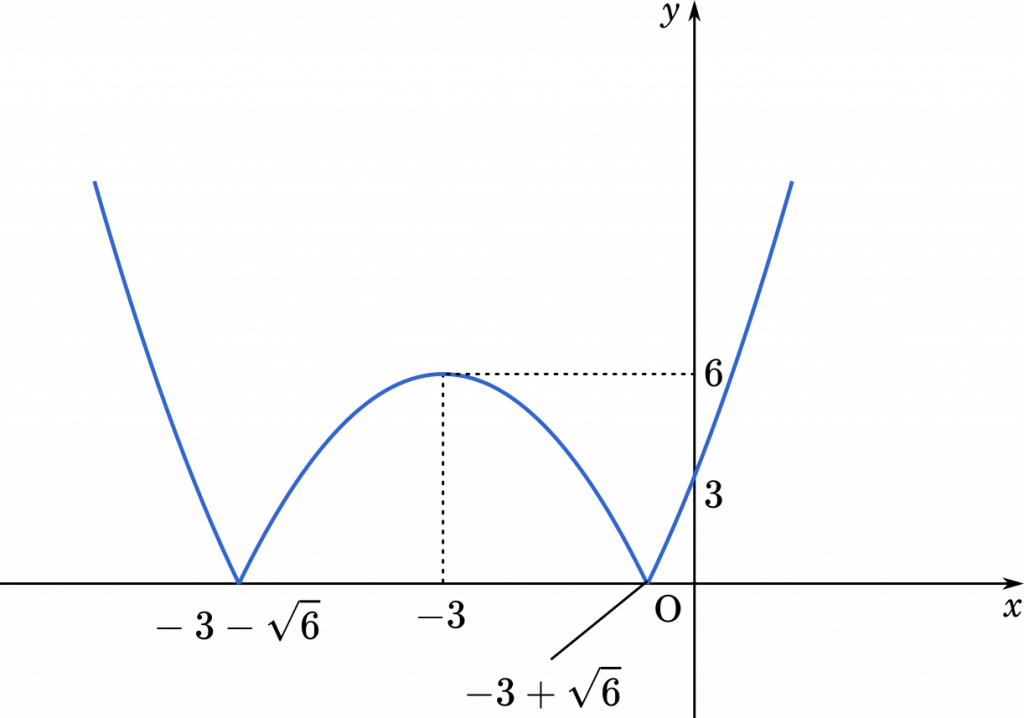
面積を求めます。ここは，2 次関数と直線で囲まれた領域になるので，6 分の 1 公式を利用しましょう。

$S=\cfrac{(\beta-\alpha)^3}{6}$
$=\cfrac{(-3+\sqrt{6}+3+\sqrt{6})^3}{6}$
$=\cfrac{(2\sqrt{6})^3}{6}$
$=\cfrac{48\sqrt{6}}{6}$
$=8\sqrt{6}$　（答え）

直線との関係

(3)に進みます。

$a=2$ とすると

$f(x)=|x^2+4x+2|$

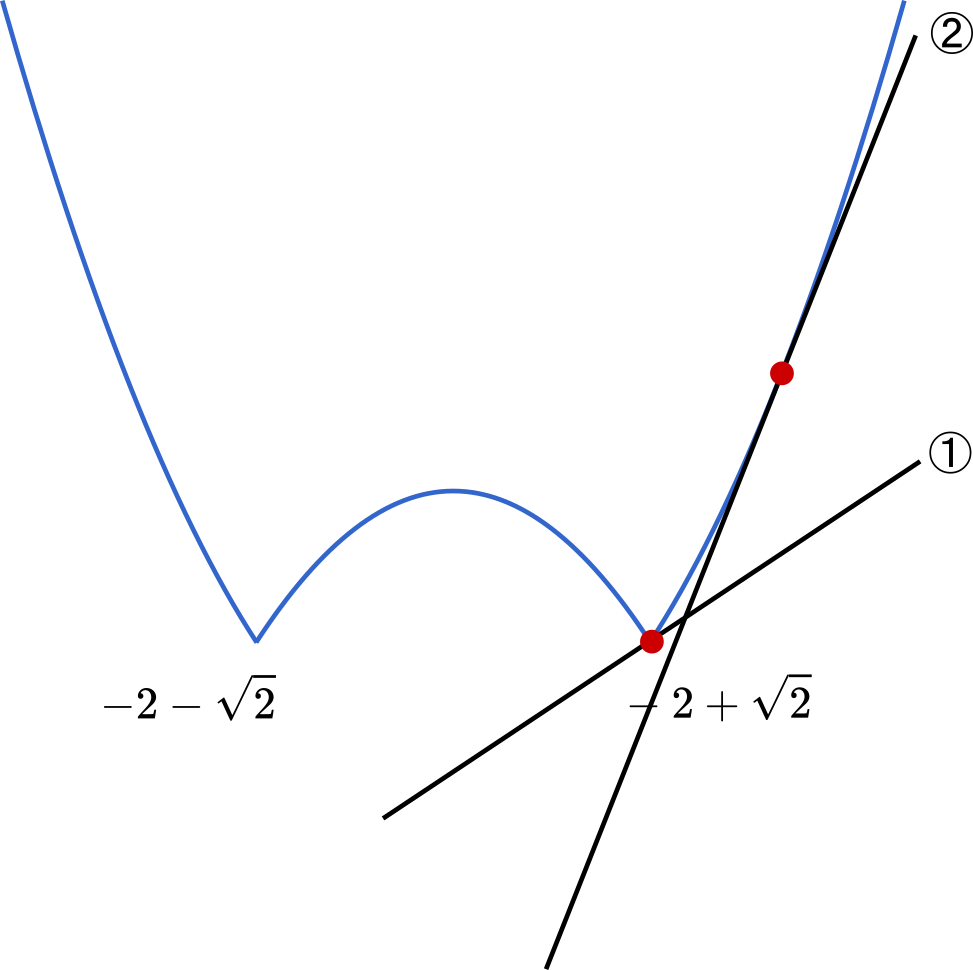
$f(x)\geqq2x+b$ ということは，曲線と直線をタテ方向で比べたとき，曲線が直線よりも上にあるということです。

$y=2x+b$ は $b$ の値によってタテ方向に平行移動するので，いろいろパターンを考えてみると，①と②の場合が考えられます。グラフはあくまで概形なので，この段階ではどちらになるかは分かりません。

②の場合について考えてみましょう。このとき，直線は曲線の接線になるので，傾きは 2 です。

$y=x^2+4x+2$ として

$y’=2x+4$

$2x+4=2$　とすると
$2x=-2$
$x=-1$

曲線と $x$ 軸の交点は

$x=-2\pm\sqrt{2^2-2}=-2\pm\sqrt{2}$

だから

$-1<-2+\sqrt{2}$

より，②の形にはなりません。

したがって，①の形で考えると，直線は $(-2+\sqrt{2},0)$ を通るので

$y\geqq ax+b$
$0\geqq2(-2+\sqrt{2})+b$
$b\leqq4-2\sqrt{2}$　（答え）