漸近線の求め方／極限を求めるのに平均値の定理を用いる問題(神戸大2018理系第2問)

$k$ を 2 以上の整数とする。また

$f(x)=\cfrac{1}{k}\Big((k-1)x+\cfrac{1}{x^{k-1}}\Big)$

とおく。以下の問に答えよ。

(1) $x>0$ において，関数 $y=f(x)$ の増減と漸近線を調べてグラフの概形をかけ。

(2) 数列 $\{x_n\}$ が $x_1>1,x_{n+1}=f(x_n)$ $(n=1,2,\cdots)$ を満たすとき，$x_n>1$ を示せ。

(3) (2)の数列 $\{x_n\}$ に対し，

$x_{n+1}-1<\cfrac{k-1}{k}(x_n-1)$

を示せ。また $\displaystyle\lim_{n\rightarrow\infty}x_n$ を求めよ。

漸近線を求める

(1)から始めます。

$f(x)=\cfrac{1}{k}\Big((k-1)x+\cfrac{1}{x^{k-1}}\Big)$
$=\cfrac{k-1}{k}x+\cfrac{1}{kx^{k-1}}$

また，式を微分すると

$f'(x)=\cfrac{1}{k}\{k-1+(1-k)x^{-k}\}$

$\cfrac{1}{k}\{k-1+(1-k)x^{-k}\}=0$ とすると両辺を $k$ 倍して

$k-1+(1-k)x^{-k}=0$
$(1-k)x^{-k}=1-k$
$x^{-k}=1$
$\cfrac{1}{x^k}=1$
$x^k=1$

$k$ は 2 以上の整数で，また $x>0$ だから，方程式が成り立つのは $x=1$ のときです。

増減表は

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|}\hline x&(0)&\cdots&1&\cdots&(\infty)\\\hline f'(x)&&-&0&+\\\hline f(x)&&\searrow&1&\nearrow\\\hline\end{array}$

$f(1)=\cfrac{1}{k}(k-1+1)=1$

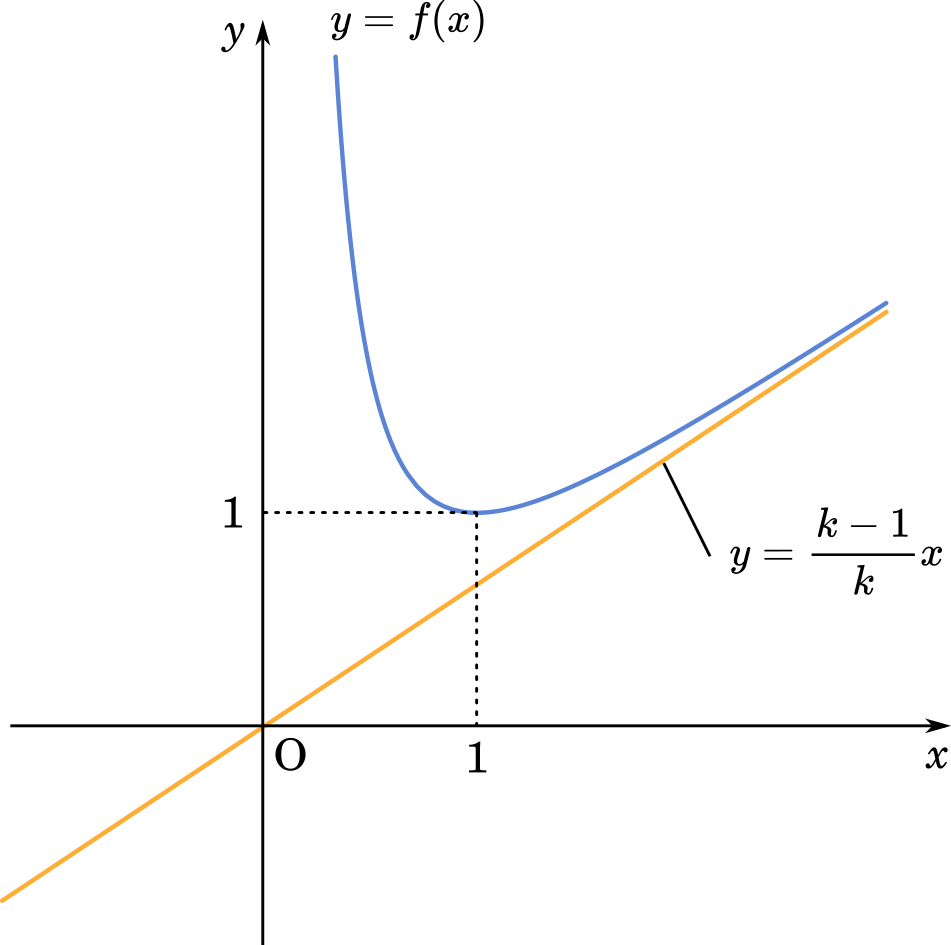
（答え）

数学的帰納法

(2)に進みます。

ここは数学的帰納法を用いて証明していきましょう。

$x_1>1$ のとき

$x_n>1$　・・・(＊)

とする。

[I] $n=1$ のとき

$x_1>1$

よって，$n=1$ のとき(＊)が成り立つ。

[II] $n=k$ のとき，(＊)が成り立つと仮定して,$n=k+1$ とすると

$x_{k+1}=f(x_k)>f(1)=1$

(1)で作ったグラフをもとに考えると，$x$ の値が 1 以上のときは $y$ も 1 以上だから，$x_k$ が 1 以上なら $x_{k+1}$ は 1 以上です。

[I]，[II] より，すべての自然数 $n$ について(＊)が成り立つ。（証明終わり）

平均値の定理を用いて極限を求める

(3)に進みます。

$x_{n+1}-1<\cfrac{k-1}{k}(x_n-1)$

を変形すると

$\cfrac{x_{n+1}-1}{x_n-1}<\cfrac{k-1}{k}$

(2)より

$\cfrac{f(x_{n})-f(1)}{x_n-1}<\cfrac{k-1}{k}$

となります。

平均値の定理より

$\cfrac{f(x_{n})-f(1)}{x_n-1}=f'(c_n)$ $(1<c_n<x_n)$

を満たす $c_n$ が存在する。

(1)より

$f'(x)=\cfrac{1}{k}\{k-1+(1-k)x^{-k}\}$

$f'(c_n)=\cfrac{1}{k}\{k-1+(1-k){c_n}^{-k}$
$=\cfrac{k-1}{k}\Big(1-\cfrac{1}{c_n}\Big)$

$1<c_n$ だから，$1-\cfrac{1}{c_n}$ は 1 より小さい値です。よって

$\cfrac{k-1}{k}\Big(1-\cfrac{1}{c_n}\Big)<\cfrac{k-1}{k}$

$f'(c_n)<\cfrac{k-1}{k}$

が成り立ちます。左辺をさかのぼっていくと

$\cfrac{x_{n+1}-1}{x_n-1}<\cfrac{k-1}{k}$

$x_{n+1}-1<\cfrac{k-1}{k}(x_n-1)$

（証明終わり）

次に極限を求めます。

(2)より $x_n>1$ だから，$x_n-1>0$ が成り立ちます。よって

$0<x_{n+1}-1<\cfrac{k-1}{k}(x_n-1)$
$0<x_n-1<\cfrac{k-1}{k}(x_{n-1}-1)$

ここで，$x_n-1=a_n$ とすると

$a_n<\cfrac{k-1}{k}a_{n-1}$ ・・・①

という関係になります。

$a_{n-1}<\cfrac{k-1}{k}a_{n-2}$
$\cfrac{k-1}{k}a_{n-1}<\Big(\cfrac{k-1}{k}\Big)^2a_{n-2}$ ・・・②

となるので，①，②より

$a_n<\cfrac{k-1}{k}a_{n-1}<\Big(\cfrac{k-1}{k}\Big)^2a_{n-2}$

これを繰り返していくと

$a_n<\cfrac{k-1}{k}a_{n-1}<\Big(\cfrac{k-1}{k}\Big)^2a_{n-2}<\cdots<\Big(\cfrac{k-1}{k}\Big)^{n-1}a_1$

$0<a_n<\Big(\cfrac{k-1}{k}\Big)^{n-1}a_1$
$0<x_n-1<\Big(\cfrac{k-1}{k}\Big)^{n-1}(x_1-1)$

$\cfrac{k-1}{k}<0$ だから

$\displaystyle\lim_{n\rightarrow\infty}\Big\{\Big(\cfrac{k-1}{k}\Big)^{n-1}(x_1-1)\Big\}=0$

はさみうちの原理より

$\displaystyle\lim_{n\rightarrow\infty}(x_n-1)=0$

$\displaystyle\lim_{n\rightarrow\infty}x_n-\lim_{n\rightarrow\infty}1=0$

$\displaystyle\lim_{n\rightarrow\infty}x_n-1=0$

したがって

$\displaystyle\lim_{n\rightarrow\infty}x_n=1$

（答え）