y=log x と 2 次関数の交点，回転体の体積，(log x)^2の積分(神戸大2016理系第3問)

$a$ を正の定数とし，2 曲線 $C_1:y=\log x$，$C_2:y=ax^2$ が点 P で接しているとする。以下の問に答えよ。

(1) P の座標と $a$ の値を求めよ。

(2) 2 曲線 $C_1,C_2$ と $x$ 軸で囲まれた部分を $x$ 軸のまわりに 1 回転させてできる立体の体積を求めよ。

交点を求める

(1)から始めます。

ます，交点の座標を P$(t,at^2)$ としましょう。

$y=\log t$ ・・・①

$y=at^2$　・・・②

ここから，2 曲線が接するところでは，接線の傾きが等しくなることを利用して，$t$ の値を求めていきます。

①を微分して

$y’=\cfrac{1}{t}$

②を微分して

$y’=2at$

式どうしを連立して

$\cfrac{1}{t}=2at$
$2at^2=1$
$t^2=\cfrac{1}{2a}$

対数関数には真数条件があるので，$\log t$ では $t>0$ となることを思い出しましょう。

$t=\cfrac{1}{\sqrt{2a}}$　・・・③

②に代入して

$y=a\cdot\cfrac{1}{2a}=\cfrac{1}{2}$

今度は①に代入します。

$\cfrac{1}{2}=\log t$

ここで対数関数の定義を思い出しましょう。

よって

$t=e^{\small{\frac{1}{2}}}=\sqrt{e}$

③に代入すると

$\cfrac{1}{\sqrt{2a}}=\sqrt{e}$

両辺を 2 乗して

$\cfrac{1}{2a}=e$

両辺の逆数をとると

$2a=\cfrac{1}{e}$
$a=\cfrac{1}{2e}$　（答え）

したがって，点 P の座標は

P$\Big(\sqrt{e},\space\cfrac{1}{2}\Big)$　（答え）

回転体の体積を求める

(2)に進みます。

回転体の体積は円の面積を積分で積み重ねて求めます。

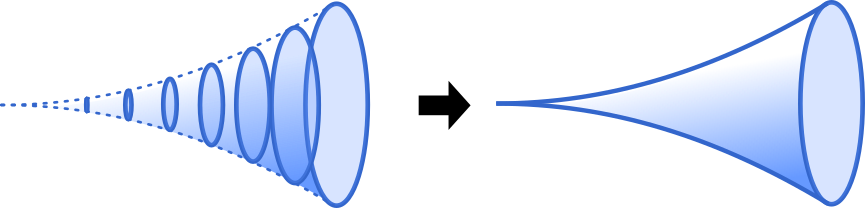
さらに 2 つの回転体を引き算すれば，問題で問われている回転体の体積を求めることができるでしょう。

円の面積は $\pi r^2$ で，グラフの $y$ 座標が円の半径です。

$\displaystyle V=\pi\int_0^{\sqrt{e}}(ax^2)^2dx-\pi\int_1^{\sqrt{e}}(\log x)^2dx$

$\displaystyle V=a^2\pi\int_0^{\sqrt{e}}x^4dx-\pi\int_1^{\sqrt{e}}(\log x)^2dx$

ここで，$\displaystyle\int(\log x)^2dx$ について

$\displaystyle\int(\log x)^2dx$
$\displaystyle=\int1\cdot(\log x)^2dx$
$\displaystyle=\int(x)’\cdot(\log x)^2dx$

$\displaystyle=x(\log x)^2-\int x\cdot2\log x\cdot\cfrac{1}{x}\space dx$

$\displaystyle=x(\log x)^2-2\int\log x\space dx$

同様に，$\log x=(x)’\log x$ として計算していきましょう。

$\displaystyle=x(\log x)^2-2\int(x)’\log x\space dx$
$\displaystyle=x(\log x)^2-2\Big\{x\log x-\int x\cdot\cfrac{1}{x}\space dx\Big\}$
$=x(\log x)^2-2x\log x+2x+C$　（$C$は積分定数）

これを用いて

$\displaystyle V=\cfrac{\pi}{4e^2}\Big[\cfrac{x^5}{5}\Big]_0^{\sqrt{e}}-\pi\Big[x(\log x)^2-2x\log x+2x\Big]_1^{\sqrt{e}}$
$=\cfrac{\pi}{4e^2}\cdot\cfrac{e^2\sqrt{e}}{5}-\pi\Big(\sqrt{e}(\log\sqrt{e})^2-2\sqrt{e}\log\sqrt{e}+2\sqrt{e}-\log1+2\log1-2\Big)$

$\log 1=0$ であることに注意して

$=\cfrac{\sqrt{e}\pi}{20}-\pi\Big(\sqrt{e}(\log e^{\small{\frac{1}{2}}})^2-2\sqrt{e}\log e^{\small{\frac{1}{2}}}+2\sqrt{e}-2\Big)$
$=\cfrac{\sqrt{e}\pi}{20}-\pi\Big\{\sqrt{e}\Big(\cfrac{1}{2}\log e\Big)^2-\sqrt{e}\log e+2\sqrt{e}-2\Big\}$

$\log e=1$ であることに注意して

$=\cfrac{\sqrt{e}\pi}{20}-\pi\Big(\cfrac{\sqrt{e}}{4}-\sqrt{e}+2\sqrt{e}-2\Big)$
$=\cfrac{\sqrt{e}\pi}{20}-\pi\Big(\cfrac{5}{4}\sqrt{e}-2\Big)$
$=\cfrac{\sqrt{e}\pi-25\sqrt{e}\pi}{20}+2\pi$
$=-\cfrac{6}{5}\sqrt{e}\pi+2\pi$
$=\Big(2-\cfrac{6}{5}\sqrt{e}\Big)\pi$　（答え）