【数III微分積分】x を定数としてみなして微分する／回転体の体積(九州大2021理系第3問)

座標平面上の点 $(x,y)$ について，次の条件を考える。

条件：すべての実数 $t$ に対して $y\leqq e^t-xt$　が成立する。・・・（＊）

以下の問いに答えよ。必要ならば $\displaystyle\lim_{x\rightarrow+0}x\log x=0$ を使ってよい。

(1) 条件（＊）をみたす点 $(x,y)$ 全体の集合を座標平面上に図示せよ。

(2) 条件（＊）をみたす点 $(x,y)$ のうち，$x\geqq1$ かつ $y\geqq0$ をみたすもの全体の集合を $S$ とする。$S$ を $x$ 軸の周りに 1 回転させてできる立体の体積を求めよ。

x を定数としてみなす

(1)から考えます。

すべての実数 $t$ に対して不等式が成り立つという条件から，$y\leqq e^t-xt$ を $x$ の関数ではなく $t$ の関数として考えると良いでしょう。

このとき，$t$ が変化し，$x$ は定数とみなします。

例えば $x=1$ と仮定して，$y=e^t-t$ とすると

$y’=e^t-1$

$e^t-1=0$ として $e^t=1$ だから $t=0$ 

増減表を作ると分かりますが，$t=0$ のときに $y$ は最小となります。

$t=0$ のとき，$y=e^0-0=1$ となるので，もともとの不等式は

$y\leqq1$

つまり，$y$ 座標が 1 より下の部分を塗りつぶすことになります。

$f(t)=e^t-xt$ として
$f'(t)=e^t-x$

$e^t-x=0$ のとき

$e^t=x$

両辺で対数をとって

$\log e^t=\log x$

このとき，真数条件から $x>0$

$t\log e=\log x$
$t=\log x$

増減表は

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|}\hline t&\cdots&\log x&\cdots\\\hline f'(t)&-&0&+\\\hline f(t)&\searrow&&\nearrow\\\hline\end{array}$
$f(\log x)=e^{\log x}-x\log x$

ここで，$e^{\log x}$ を整理しておきます。

$e^{\log x}=k$ として

$e$ の $\log x$ 乗が $k$ であるという関係を対数で表すと，次の式が出来上がります。

$\log k=\log x$
$x=k$

よって

$f(\log x)=x-x\log x$

$e^t-xt$ の最小値が $x-x\log x$ であるということは

$y=x-x\log x$ が領域の境界であるということです。ただし，これは $x>0$ の範囲においてです。
他の場合も考えてみましょう。

・$x=0$ のとき

$y\leqq x-x\log x$

を考えると，問題文の条件

$\displaystyle\lim_{x\rightarrow+0}x\log x=0$

より

$y\leqq0$

となります。

・$x<0$ のとき

$f'(t)=e^t-x$ から考えると，すべての実数 $t$ において，$f'(t)$ は正の数となります。つまり，$f(t)$ は単調増加です。このとき

$\displaystyle\lim_{t\rightarrow-\infty}f(t)=-\infty$

となり

$y\leqq-\infty$

をみたす $y$ の値は存在しません。

したがって

$y\leqq x-x\log x$ $(x>0)$
$y\leqq 0$ $(x=0)$

ここで，$x$ 軸との交点を求めておきましょう。

$x-x\log x=0$ とすると

$x(1-\log x)=0$

$1-\log x=0$ のとき

$\log x=1$
$x=e$

よって，$x=0,e$

また，グラフの最大となる点は

$g(x)=x-x\log x$ として

$g'(x)=1-\Big(\log x+x\cdot\cfrac{1}{x}\Big)$
$=-\log x$

$-\log x=0$ のとき

$x=1$

$g(1)=1-\log 1=1$

よって，グラフが最大となる点は $(x,y)=(1,1)$ です。

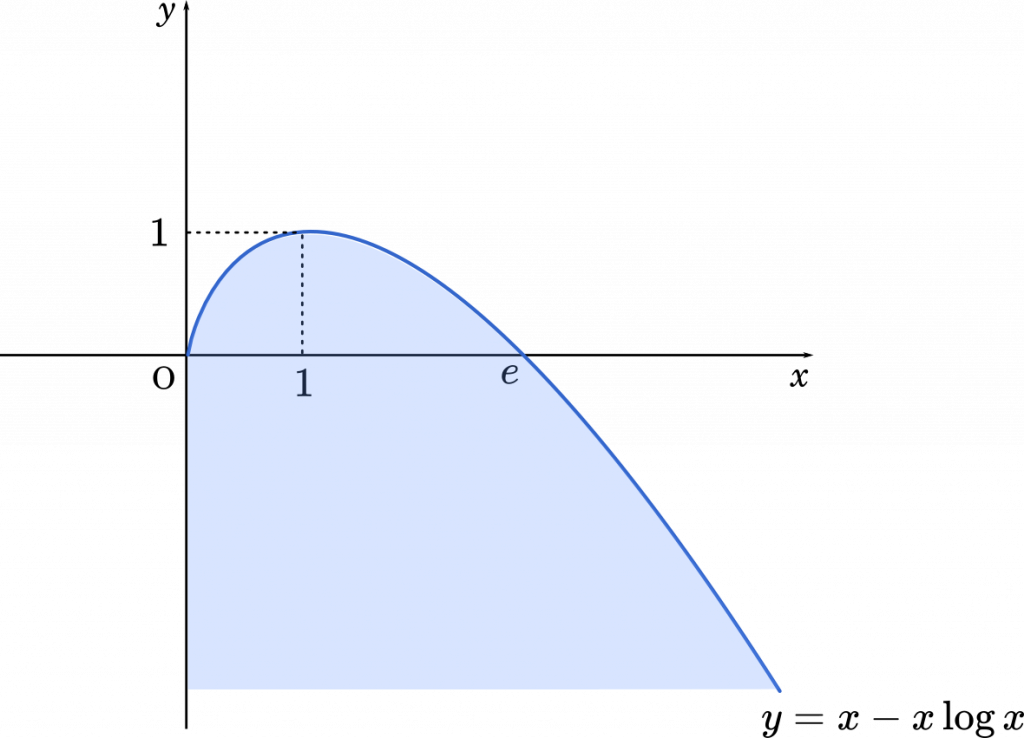
（答え）

回転体の体積を求める

(2)に進みます。

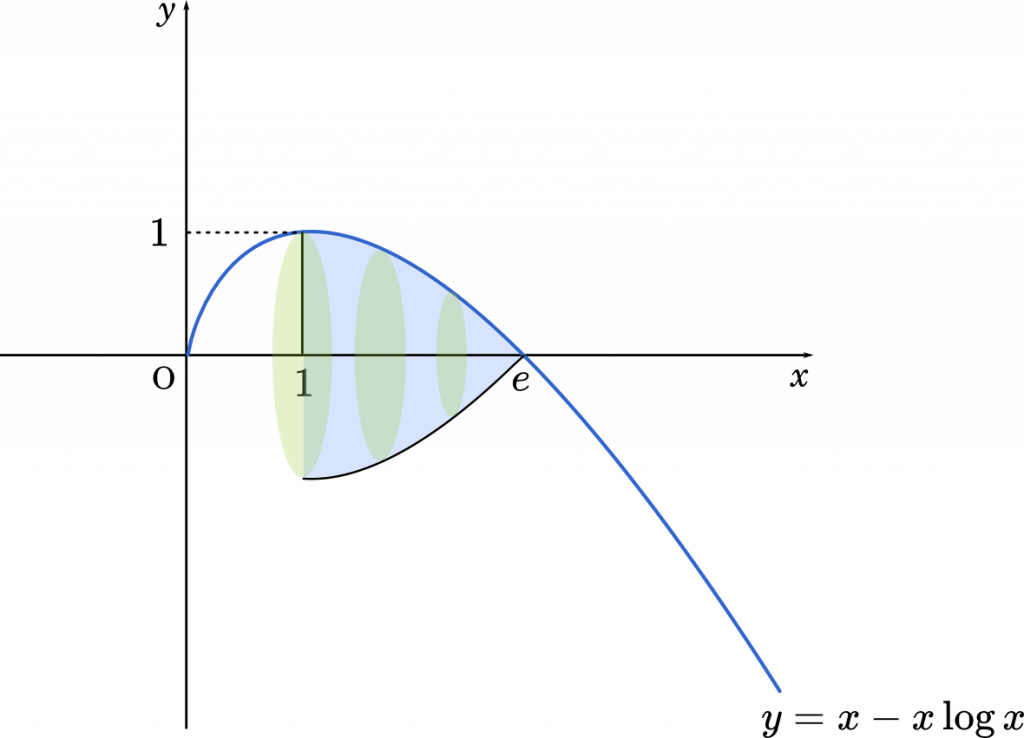
回転体の体積は，断面の円の面積を積分して求めます。

断面の円の面積は

$S=\pi r^2$
$=\pi(x-x\log x)^2$
$\pi\{x^2-2x^2\log x+x^2(\log x)^2\}$

回転体の体積は

$\displaystyle S=\pi\int_1^e x^2-2x^2\log x+x^2(\log x)^2\space dx$

一度に計算するとタイヘンなので，分けて計算していきます。

$\displaystyle \int x^2\space dx$
$=\cfrac{x^3}{3}+C_1$

$\displaystyle\int2x^2\log x\space dx$

式がかけ算なので，部分積分を用います。

$\displaystyle=2\int\Big(\cfrac{x^3}{3}\Big)’\log x\space dx$
$\displaystyle =2\Big\{\cfrac{x^3}{3}\log x-\int\cfrac{x^3}{3}\cdot\cfrac{1}{x}\space dx\Big\}$
$\displaystyle=\cfrac{2}{3}x^3\log x-\cfrac{2}{3}\int x^2\space dx$
$=\cfrac{2}{3}x^3\log x-\cfrac{2}{9}x^3+C_2$

$\displaystyle\int x^2(\log x)^2\space dx$
$\displaystyle=\int\Big(\cfrac{x^3}{3}\Big)'(\log x)^2\space dx$
$\displaystyle=\cfrac{x^3}{3}(\log x)^2-\int\cfrac{x^3}{3}\cdot2(\log x)\cdot\cfrac{1}{x}\space dx$

$\displaystyle=\cfrac{x^3}{3}(\log x)^2-\cfrac{1}{3}\int 2x^2\log x\space dx$

ここで，先ほど積分した結果を利用しましょう。

$\displaystyle=\cfrac{x^3}{3}(\log x)^2-\cfrac{1}{3}\Big(\cfrac{2}{3}x^3\log x-\cfrac{2}{9}x^3\Big)$
$\displaystyle=\cfrac{x^3}{3}(\log x)^2-\cfrac{2}{9}x^3\log x-\cfrac{2}{27}x^3+C_3$

($C_1,C_2,C_3$は積分定数)

よって

$V=\pi\Big[\cfrac{x^3}{3}-\cfrac{2}{3}x^3\log x+\cfrac{2}{9}x^3+\cfrac{x^3}{3}(\log x)^2-\cfrac{2}{9}x^3\log x+\cfrac{2}{27}x^3\Big]_1^e$
$=\pi\Big[\cfrac{17}{27}x^3-\cfrac{8}{9}x^3\log x+\cfrac{x^3}{3}(\log x)^2\Big]_1^e$
$=\pi\Big(\cfrac{17}{27}e^3-\cfrac{8}{9}e^3+\cfrac{1}{3}e^3-\cfrac{17}{27}\Big)$
$=\cfrac{27}{\pi}(17e^3-24e^3+9e^3-17)$
$=\cfrac{\pi}{27}(2e^3-17)$ （答え）