x 軸に平行なベクトルを方向ベクトルで表す／回転体の体積(横浜国立大2020理系第4問)

$xyz$ 空間に，2 点 A$(1,2,9)$，B$(-3,6,7)$ を通る直線 $\ell$ がある。また，$\ell$ 上の点 P，Q と，$x$ 軸上の点 R，S は

直線 PR $\perp$ $xy$ 平面，直線 QS $\perp$ $x$ 軸，直線 QS $\perp$ $\ell$ 

をみたす。次の問いに答えよ。

(1) P，R の座標を求めよ。

(2) Q，S の座標を求めよ。

(3) 線分 PQ を $x$ 軸のまわりに 1 回転してできる曲面と，P を含み $x$ 軸に垂直な平面と，Q を含み $x$ 軸に垂直な平面で囲まれた立体の体積を求めよ。

ベクトル方程式

(1)から始めます。

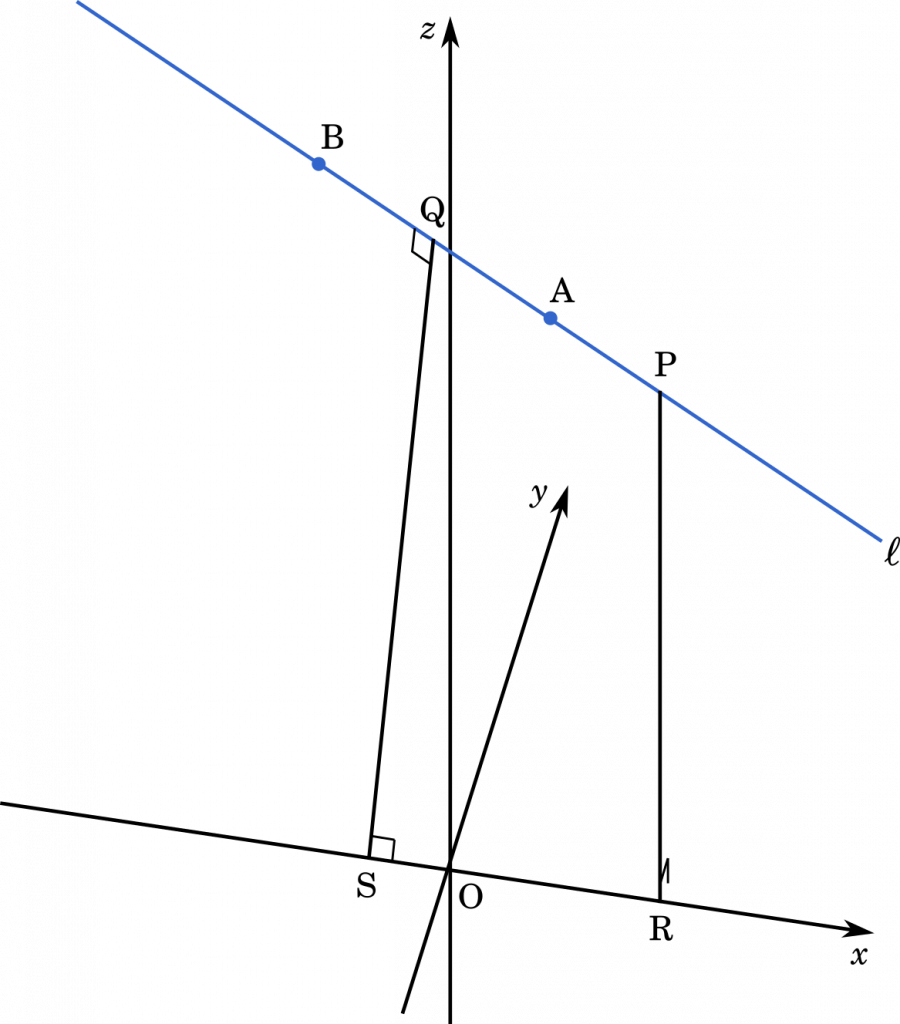
点 P は直線 $\ell$ 上にあるので，これをベクトル方程式として表してみます。

$\overrightarrow{\text{OP}}=\overrightarrow{\text{OA}}+k\overrightarrow{\text{AB}}$ として

$\overrightarrow{\text{AB}}=\overrightarrow{\text{OB}}-\overrightarrow{\text{OA}}$
$=(-3,6,7)-(1,2,9)$
$=(-4,4,-2)$

$\overrightarrow{\text{OP}}=(1,2,9)+k(-4,4,-2)$
$=(-4k+1,4k+2,-2k+9)$

点 P は $y$ 座標が 0 だから

$4k+2=0$
$k=-\cfrac{1}{2}$

したがって

$\text{P}(3,0,10)$

さらに，点 R　は $x$ 軸上にあるので，$y$ 座標と $z$ 座標が 0 の点です。

したがって

$\text{R}(3,0,0)$　（答え）

x 軸をベクトルで表す

(2)に進みます。

まず，直線 QS $\perp$ $\ell$ から

$\overrightarrow{\text{AB}}\cdot\overrightarrow{\text{QS}}=0$

という式を作ることができます。

あともう一つ

直線 QS $\perp$ $x$ 軸

という条件から，式を作ります。

点 Q もまた，$\ell$ 上の点なので，(1)と同様にベクトル方程式を作ってみます。

$\overrightarrow{\text{OQ}}=\overrightarrow{\text{OA}}+k\overrightarrow{\text{AB}}$ として

$=(-4k+1,4k+2,-2k+9)$

S の座標が分からないので $t$ としてみます。

$\overrightarrow{\text{OS}}=(t,0,0)$ として

$\overrightarrow{\text{QS}}=\overrightarrow{\text{OS}}-\overrightarrow{\text{OQ}}$
$=(t+4k-1,-4k-2,2k-9)$

これを用いて

$\overrightarrow{\text{AB}}\cdot\overrightarrow{\text{QS}}=-4(t+4k-1)+4(-4k-2)-2(2k-9)=0$
$-4t-16k+4-16k-8-4k+18=0$
$18k+2t=7$　・・・①

また

$\overrightarrow{\text{QS}}\cdot\overrightarrow{\text{OS}}=t(t+4k-1)=0$

$t=0$ または

$t+4k-1=0$ より

$t=-4k+1$

ここで，解が 2 個になったのは $\overrightarrow{\text{OS}}=(t,0,0)$ としたことが原因です。

解の一つは $t=0$ ですが，これはいわゆる零ベクトルです。零ベクトルは何をかけても 0 になるのだから，内積が 0 になるのは当たり前のことです。しかし，それによって，垂直であることを示すことはできません。

たとえば，上で作った $\overrightarrow{\text{OQ}}=\overrightarrow{\text{OA}}+k\overrightarrow{\text{AB}}$ の $\overrightarrow{\text{AB}}$ の部分が方向ベクトルです。このベクトルはベクトルの向きを表していて，それを $k$ 倍することで $\overrightarrow{\text{AB}}$ に平行なさまざまなベクトルを表すことができます。

同じように，$x$ 軸に平行なベクトルを，たとえば $(1,0,0)$ として表すことで $x$ 軸の代わりに用いることができます。

$x$ 軸に平行なベクトルを $(1,0,0)$ として，$\overrightarrow{\text{QS}}$ との内積を求めると

$1\cdot(t+4k-1)+0\cdot(-4k-2)+0\cdot(2k-4)$
$=t+4k-1=0$

よって

$4k+t=1$　・・・②

①，②を連立すると

$\begin{aligned}18k+2t=7\\-)8k+2t=2\\\hline10k=5\\k=\cfrac{1}{2}\end{aligned}$

②に代入して

$4\cdot\cfrac{1}{2}+t=1$
$t=-1$

したがって

Q$(-1,4,8)$
S$(-1,0,0)$

（答え）

回転体の体積

(3)に進みます。

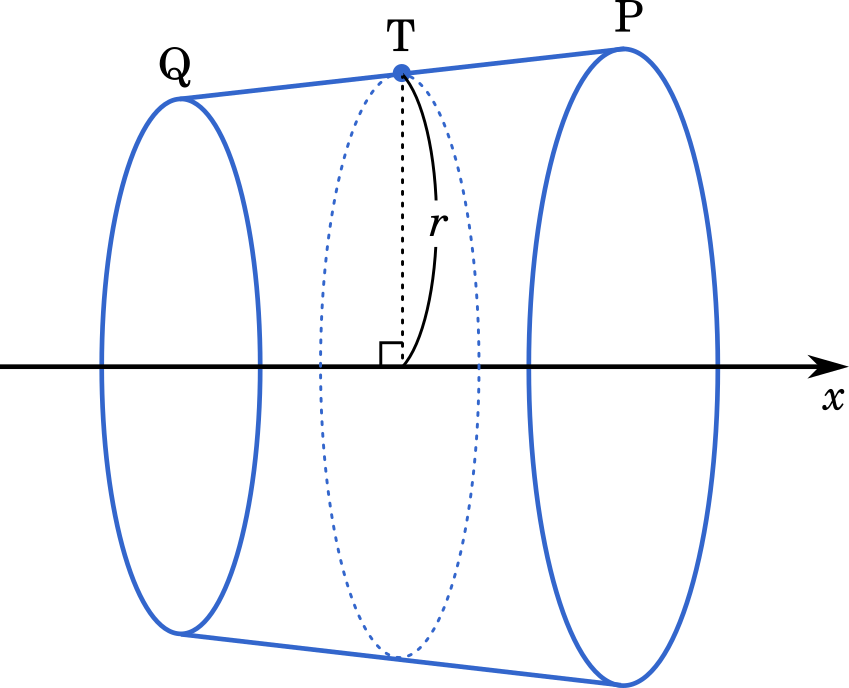
直線 QP のあいだに点 T を作って，これが Q から P まで移動しながら，円の面積を積分で積み上げていくイメージです。

(1)と(2)で求めた Q，P の座標から積分区間は $[-1,3]$ です。したがって，体積は

$\displaystyle\int_{-1}^3\pi r^2\space dx$

と表されます。次に，$r^2$ の式を作ってみます。

点 T は QP 上の点だから，同様にベクトル方程式で表してみましょう。

直線 QP 上の点を T とすると

$\overrightarrow{\text{OT}}=\overrightarrow{\text{OQ}}+k\overrightarrow{\text{QP}}$

ここで $\overrightarrow{\text{QP}}$ は

$\overrightarrow{\text{QP}}=\overrightarrow{\text{OP}}-\overrightarrow{\text{OQ}}$
$=(3+1,0-4,10-8)$
$=(4,-4,2)$

となるので

$\overrightarrow{\text{OT}}=(-1,4,8)+k(4,-4,2)$
$=(4k-1,-4k+4,2k+8)$

よって，三平方の定理より

$r^2=(-4k+4)^2+(2k+8)^2$

$=16k^2-32k+16+4k^2+32k+64$
$=20(k^2+4)$

体積は

$\displaystyle V=20\pi\int_{-1}^3k^2+4\space dx$

$x=4k-1$　とすると

$dx=4\space dk$

$\def\arraystretch{1.5}\begin{array}{|c|c|}\hline x&-1\rightarrow3\\\hline k&0\rightarrow1\\\hline\end{array}$

$V=\displaystyle20\pi\int_0^1(k^2+4)\cdot4\space dk$
$=\displaystyle80\pi\int_0^1k^2+4\space dk$
$=80\pi\Big[\cfrac{k^3}{3}+4k\Big]_0^1$
$=80\pi\cdot\cfrac{13}{3}$
$=\cfrac{1040}{3}\pi$　（答え）