x が 0 以上と 0 未満で積分する式が異なる問題(東京都立大2018文系第1問)

関数

$f(x)=\begin{cases}2x\space(x\geq0\sf{のとき})\\-x\space(x<0\sf{のとき})\end{cases}$

について，以下の問いに答えなさい。（東京都立大2018）

(1) $y=f(x)$ のグラフをかきなさい。

(2) $\displaystyle g(x)=\int_x^{x+1}f(t)\space dt$ とおく。$g(x)$ を求めなさい。

(3) (2)の関数 $g(x)$ の最小値を求めなさい。

２つの直線があるグラフ

(1)はグラフを描けば終わりです。

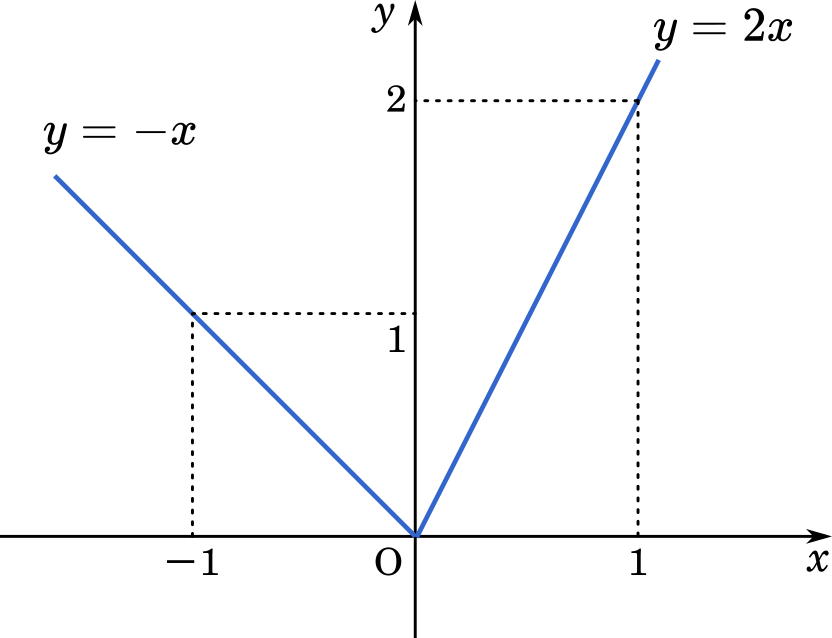
x の範囲によって式を分ける

(2)に進みます。ここでは，$x$ の範囲にって積分する式が変わるので注意が必要です。

(i) $x+1<0$ のとき

$x<-1$

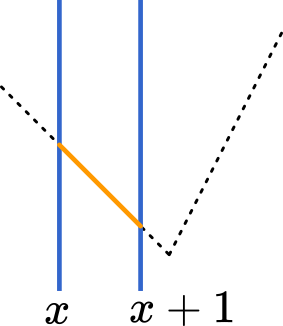
図を描いてみると，このような場合なら $f(x)=-x$ を積分すれば良いことが分かります。
$\displaystyle g(x)=\int_x^{x+1}-t\space dt$

$=\Big[-\cfrac{t^2}{2}\Big]_x^{x+1}$
$=-\cfrac{1}{2}\Big\{(x+1)^2-x^2\Big\}$
$=-\cfrac{1}{2}(2x+1)$
$=-x-\cfrac{1}{2}$

(ii) $-1\leqq x<0$ のとき

今度は $x=0$ で式が変わるので，積分の式を２つ作り，足し合わせます。

$\displaystyle g(x)=\int_x^0-t\space dt+\int_0^{x+1}2t\space dt$
$=\Big[-\cfrac{1}{2}t^2\Big]_x^0+\Big[t^2\Big]_0^{x+1}$
$=\cfrac{1}{2}x^2+(x+1)^2$
$=\cfrac{3}{2}x^2+2x+1$

(iii) $x\geqq0$ のとき

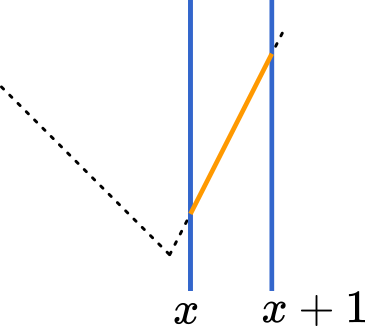
$\displaystyle g(x)=\int_x^{x+1}2t\space dt$
$=\Big[t^2\Big]_x^{x+1}$
$=(x+1)^2-x^2=2x+1$

したがって

$\begin{cases}-x-\cfrac{1}{2}\space(x<-1\space\sf{のとき})\\\cfrac{3}{2}x^2+2x+1\space(-1\leqq1<0\space\sf{のとき})\\2x+1\space(x\geqq1\space\sf{のとき})\end{cases}$

（答え）

最小値を求める

(3)に進みます。(2)で求めた 3 つのグラフをつなげるとこのようになります。

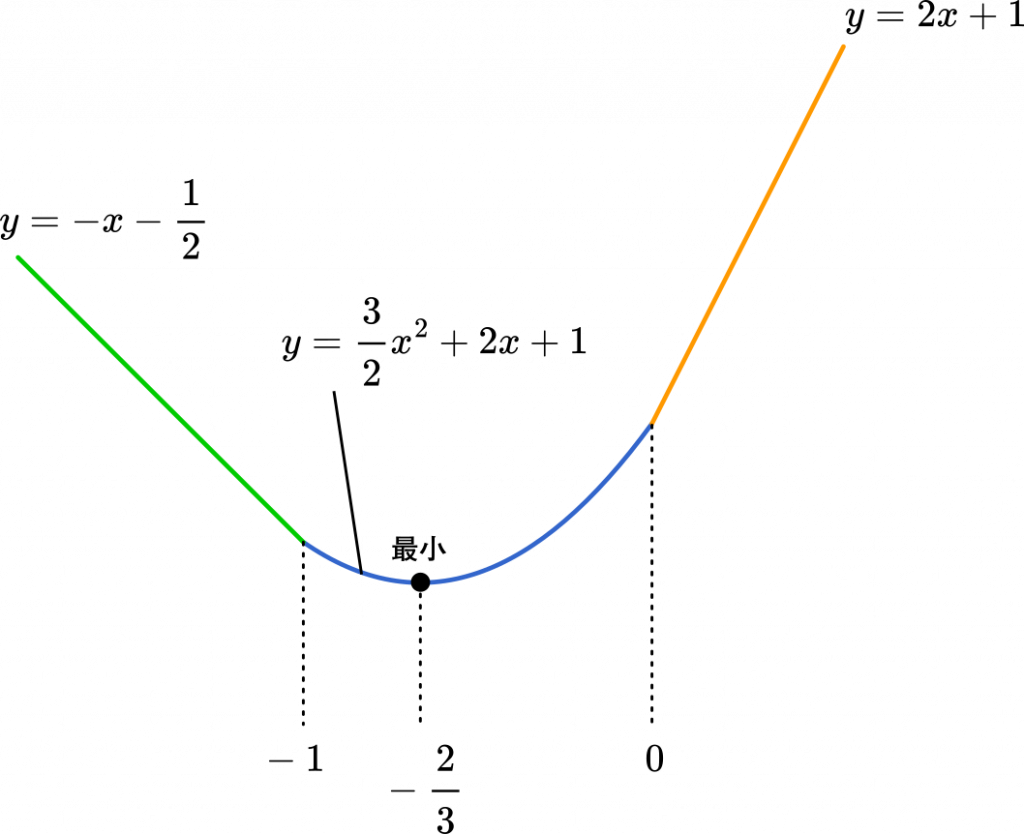
最小となる点を求めましょう。

$\cfrac{3}{2}x^2+2x+1$ を平方完成して
$=\cfrac{3}{2}\Big(x^2+\cfrac{4}{3}x\Big)+1$
$=\cfrac{3}{2}\Big(x+\cfrac{2}{3}\Big)^2-\cfrac{3}{2}\cdot\cfrac{4}{9}+1$
$=\cfrac{3}{2}\Big(x+\cfrac{2}{3}\Big)^2+\cfrac{1}{3}$

したがって，最小値は $x=-\cfrac{2}{3}$ のとき $\cfrac{1}{3}$ （答え）