直交する２本の接線に囲まれた面積とその最小値(東京都立大2020文系第4問)

関数 $f(x)=2ax-x^2$　$\Big(a>\cfrac{1}{2}\Big)$ に対し，原点 O における曲線 $y=f(x)$ の接線を $l$ とする。$t$ を実数とし，点 $(t,f(t))$ における曲線 $y=f(x)$ の接線を $m$ とする。2 つの接線 $l$ と $m$ が直交しているとき，以下の問いに答えなさい。

(1) $t$ を $a$ を用いて表しなさい。

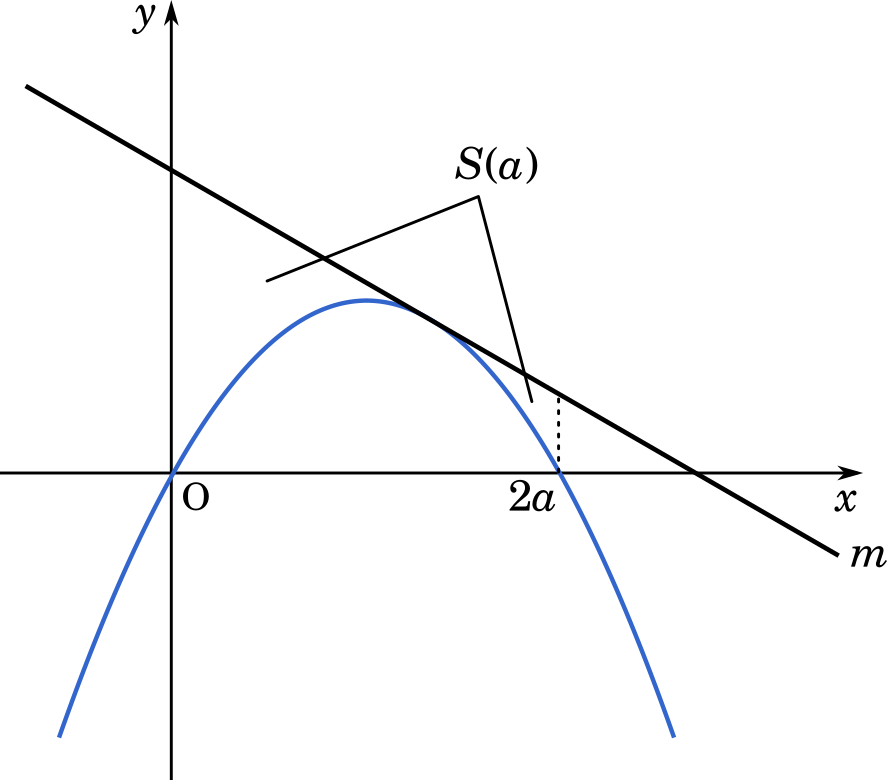
(2) 曲線 $y=f(x)$ と接線 $m$ と 2 直線 $x=0$，$x=2a$ で囲まれた図形の面積 $S(a)$ を求めなさい。

(3) $a>\cfrac{1}{2}$ のとき，$\cfrac{S(a)}{a}$ の最小値を求めなさい。また，そのときの $a$ の値を求めなさい。

接線の式を求める

(1)から始めます。

まず，接線 $l$ の式を作ってみましょう。

$f'(x)=2a-2x$

$x=0$ のとき

$f'(0)=2a$

接線 $l$ は，原点を通り，傾き $2a$ の直線。よって

$l:y=2ax$

次に接線 $m$ を作ります。

点 $(t,f(t))$ における接線の傾きは

$f'(t)=2a-2t=2(a-t)$

接線 $m$ は

$m:y-f(t)=2(a-t)(x-t)$
$y=2(a-t)(x-t)+2at-t^2$
$=2(a-t)x-2t(a-t)+2at-t^2$
$=2(a-t)x-2at+2t^2+2at-t^2$
$=2(a-t)x+t^2$

ここで，2 本の直線が垂直に交わるとき，直線の傾きどうしをかけると $-1$ になることを思い出しましょう。

$2a\times2(a-t)=-1$
$4a^2-4at=-1$
$4at=4a^2+1$
$t=a+\cfrac{1}{4a}$　（答え）

積分して面積を求める

(2)に進みます。

いったん，おおまかなグラフを描いておいた方が良いでしょう。

$f(x)$ を平方完成すると

$f(x)=2ax-x^2$　$\Big(a>\cfrac{1}{2}\Big)$
$=-(x^2-2ax)$
$=-(x-a)^2+a^2$

また $f(x)=0$ となるとき

$2ax-x^2=0$
$x(2a-x)=0$
$x=0,2a$

さらに，$t$ と $2a$ を比べると，$t=a+\cfrac{1}{4a}$ であり，$\cfrac{1}{4a}<a$ であることを考えると，$t<2a$ であることが分かります。

$\displaystyle S(a)=\int_0^{2a}2(a-t)x+t^2-2ax+x^2\space dx$
$\displaystyle=\int_0^{2a}-2tx+t^2+x^2\space dx$
$=\Big[-tx^2+t^2x+\cfrac{x^3}{3}\Big]_0^{2a}$
$=-4a^2t+2at^2+\cfrac{8}{3}a^3$
$=-4a^2\Big(a+\cfrac{1}{4a}\Big)+2a\Big(a+\cfrac{1}{4a}\Big)^2+\cfrac{8}{3}a^3$
$=-4a^3-a+2a\Big(a^2+\cfrac{1}{2}+\cfrac{1}{16a^2}\Big)+\cfrac{8}{3}a^3$
$=-4a^3-a+2a^3+a+\cfrac{1}{8a}+\cfrac{8}{3}a^3$
$=\cfrac{2}{3}a^3+\cfrac{1}{8a}$　（答え）

相加・相乗平均

(3)に進みます。

$\cfrac{S(a)}{a}=\cfrac{2}{3}a^2+\cfrac{1}{8a^2}$

式を通分してみると，$\cfrac{16a^4+3}{24a^2}$ となり，分母と分子に $a$ がある状態です。そして，これ以上整理できそうにありません。分母か分子のどちらか一方にだけ $a$ がある状態であれば，そこから最小値や最大値を考えることができるのですが，それができないときは相加相乗平均の可能性を疑ってみましょう。

相加・相乗平均より

$\cfrac{2}{3}a^2+\cfrac{1}{8a^2}\geqq2\sqrt{\cfrac{2}{3}a^2\cdot\cfrac{1}{8a^2}}$
$\geqq2\sqrt{\cfrac{1}{12}}$
$\geqq2\cfrac{1}{2\sqrt{3}}$
$\geqq\cfrac{\sqrt{3}}{3}$

したがって，最小値は $\cfrac{\sqrt{3}}{3}$

このとき

$\cfrac{2}{3}a^2=\cfrac{1}{8a^2}$
$a^4=\cfrac{3}{16}$

$a$ は正の数だから

$a^2=\cfrac{\sqrt{3}}{4}$
$a=\cfrac{\sqrt[4]{3}}{2}$　（答え）