【高校数学・数列】特性方程式はどうして引き算するのか? ざっくりイメージで理解する





特定方程式のおさらい
例題 $a_1=1,\space a_{n+1}=3a_n+4$ の一般項を求めよ。
こういう形を $pa_n+q$ 型の漸化式といいます。このとき $\alpha=3\alpha+4$ という式(特性方程式)を作って引き算をします。
$\begin{matrix}&a_{n+1}&=&3a_n+4\\-)&\alpha&=&3\alpha+4\\\hline &a_{n+a}-\alpha&=&3(a_n-\alpha)&\cdots\text{①}\end{matrix}$
次に $\alpha$ を求めます。
$\alpha=3\alpha+4$
$\alpha=-2$
よって①は
$a_{n+1}+2=3(a_n+2)$
ここで $a_n+2=b_n$ として
$b_{n+1}=3b_n$
よって $b_n$ は等比数列である。
また、$b_1=a_1+2=1+2=3$ だから、$b_n$ の一般項を求めると
$b_n=3\cdot 3^{n-1}=3^n$
$a_n+2=3^n$
$a_n=3^n-2$(答え)

数列が2階建てになる
例題でやったように、特性方程式を作ったあとに引き算をします。ここでやっていることの意味をおおまかなイメージで説明しましょう。
まず、例題の答えは $a_n=3^n-2$ となっていて、形としては 等比数列+定数 の形になっています。
この数列を関数のように考えて $y=3^x-2$ とするとグラフは以下のようになります。
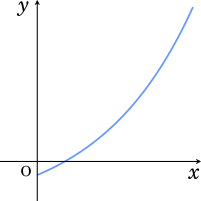
このグラフは2階建て構造になっていて、等比数列と階差数列に分けることができます。
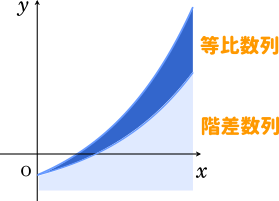
さらにこの階差数列は 等比数列+定数 という形になっています。
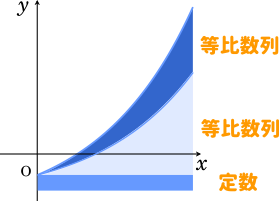

そして、この2つの等比数列は同じものになります。よって、等比数列+定数 となります。
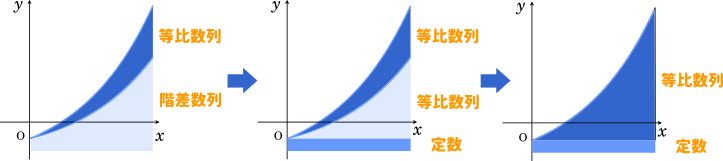




根拠となる数式
最後に、今回の解説の根拠となる式を紹介します。
$a_{n+1}=pa_n+q$ のとき、各項を求めると
$a_1=a_1$
$a_2=a_1 p+q$
$a_3=p(a_1 p+q)+q$
$=a_1 p^2+qp+q$
$a_4=p(a_1 p^2+qp+q)+q$
$=a_1 p^3+qp^2+qp+q$
$a_n=a_1 p^{n-1}+qp^{n-2}+qp^{n-3}+\cdots+qp+q$
ここから、$qp^{n-2}+qp^{n-3}+\cdots+qp+q$ の部分は階差数列であり、初項 $q$、公比 $p$ の等比数列の和であることが分かる。したがって
$\displaystyle a_n=a_1 p^{n-1}+q+q\sum_{k=1}^{n-2} p^k$
$\displaystyle =a_1 p^{n-1}+q+q\frac{p(1-p^{n-2})}{1-p}$
$\displaystyle =a_1 p^{n-1}+q+\frac{1}{1-p}(qp-qp^{n-1})$
式を$p^{n-1}$ についてまとめると
$\displaystyle =\frac{(1-p)a_1 p^{n-1}-qp^{n-1}}{1-p}+q+\frac{qp}{1-p}$
$\displaystyle =p^{n-1}\frac{(1-p)a_1-q}{1-p}+q+\frac{qp}{1-p}$
ここで $\alpha=\alpha p+q$ とおくと
$\alpha-\alpha p=q$
$\displaystyle \alpha=\frac{q}{1-p}$
これを式に代入すると
$=(a_1-\alpha)p^{n-1}+\alpha p+q$
よって、式は 等比数列+定数 の形になる。
SNSでシェア