【複素数平面】点を60°回転して正三角形を作る方法／3点が一直線であることの証明(東京都立大2017理系第2問)

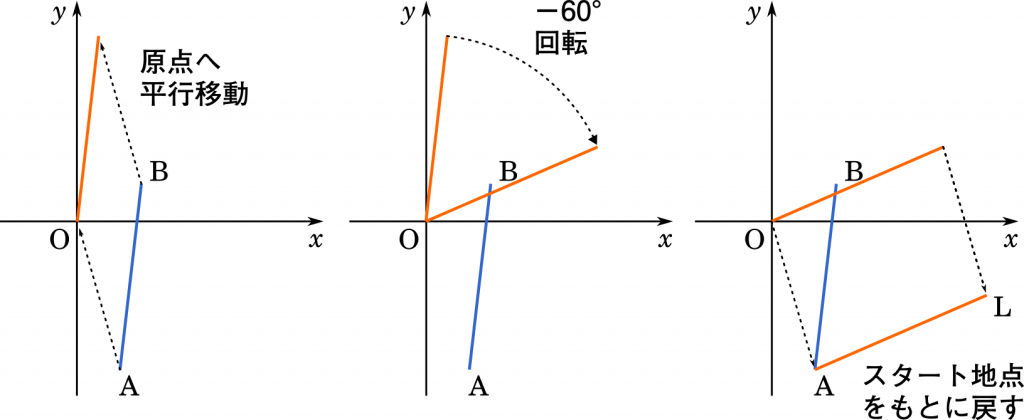
①　直線を原点に平行移動します。B の座標から A の座標を引くと，原点に移動します。

複素数平面上における回転は原点を中心とする回転しかできないので，直線をいったん原点に移動させないと回転できません。

②　極形式をかけて回転させます。複素数平面ではかけ算＝回転です。

③　回転した直線をもとの位置に戻します。

演習問題

複素数平面上の原点 O と 2 点 A$(2-4\sqrt{3}i)$，B$(3+\sqrt{3}i)$ を考える。ただし，$i$ を虚数単位とする。三角形 OAB の外側に，3 辺 AB，BO，OA をそれぞれ 1 辺とする正三角形 ALB，BMO，ONA を作る。以下の問いに答えなさい。（東京都立大2017）

(1) 点 L，M，N を表す複素数をそれぞれ求めなさい。

(2) 直線 OL と直線 AM の交点を P とする。点 P を表す複素数を求めなさい。

(3) 3 点 B，P，N が一直線上にあることを示しなさい。

極形式を複素数に変換して計算する

(1)から始めます。

上で説明した手順で辺 AB を $-60\degree$ 回転させて点 L を求めます。

①　引き算で原点に平行移動

$3+\sqrt{3}i-(2-4\sqrt{3}i)$

②　かけ算で回転

極形式で表すと

$\times\Big\{\cos\Big(-\cfrac{\pi}{3}\Big)+i\sin\Big(-\cfrac{\pi}{3}\Big)\Big\}$

となります。

③　もとの位置に戻す

$+2-4\sqrt{3}i$

これらを合わせると

$(3+\sqrt{3}i-2+4\sqrt{3}i)\Big\{\cos\Big(-\cfrac{\pi}{3}\Big)+i\sin\Big(-\cfrac{\pi}{3}\Big)\Big\}+2-4\sqrt{3}i$
$=(1+5\sqrt{3}i)\Big(\cfrac{1}{2}-\cfrac{\sqrt{3}}{2}i\Big)+2-4\sqrt{3}i$

極形式を複素数になおしても，式が表す値は同じです。かけ算をすればちゃんと回転になります。

$=\cfrac{1}{2}(1+5\sqrt{3}i)(1-\sqrt{3}i\Big)+2-4\sqrt{3}i$
$=\cfrac{1}{2}(1-\sqrt{3}i+5\sqrt{3}i+15)+2-4\sqrt{3}i$
$=\cfrac{1}{2}(16+4\sqrt{3}i)+2-4\sqrt{3}i$
$=8+2\sqrt{3}i+2-4\sqrt{3}i$
$=10-2\sqrt{3}i$

同じ手順で点 M を求めます。

$(3+\sqrt{3}i)\Big(\cos\cfrac{\pi}{3}+i\sin\cfrac{\pi}{3}\Big)$
$=(3+\sqrt{3}i)\Big(\cfrac{1}{2}+\cfrac{\sqrt{3}}{2}i\Big)$
$=\cfrac{1}{2}(3+\sqrt{3}i)(1+\sqrt{3}i)$
$=\cfrac{1}{2}(3+3\sqrt{3}i+\sqrt{3}i-3)$
$=2\sqrt{3}i$

さらに，点 N を求めます。

$(2-4\sqrt{3}i)\Big\{\cos\Big(-\cfrac{\pi}{3}\Big)+i\sin\Big(-\cfrac{\pi}{3}\Big)\Big\}$
$=(2-4\sqrt{3}i)\Big(\cfrac{1}{2}-\cfrac{\sqrt{3}}{2}i\Big)$
$=\cfrac{1}{2}(2-4\sqrt{3}i)(1-\sqrt{3}i)$
$=(1-2\sqrt{3}i)(1-\sqrt{3}i)$
$=1-\sqrt{3}i-2\sqrt{3}i-6$
$=-5-3\sqrt{3}i$

したがって

L $(10-2\sqrt{3}i)$
M $(2\sqrt{3}i)$
N $-5-3\sqrt{3}i$　（答え）

複素数平面の内分点

(2)に進みます。

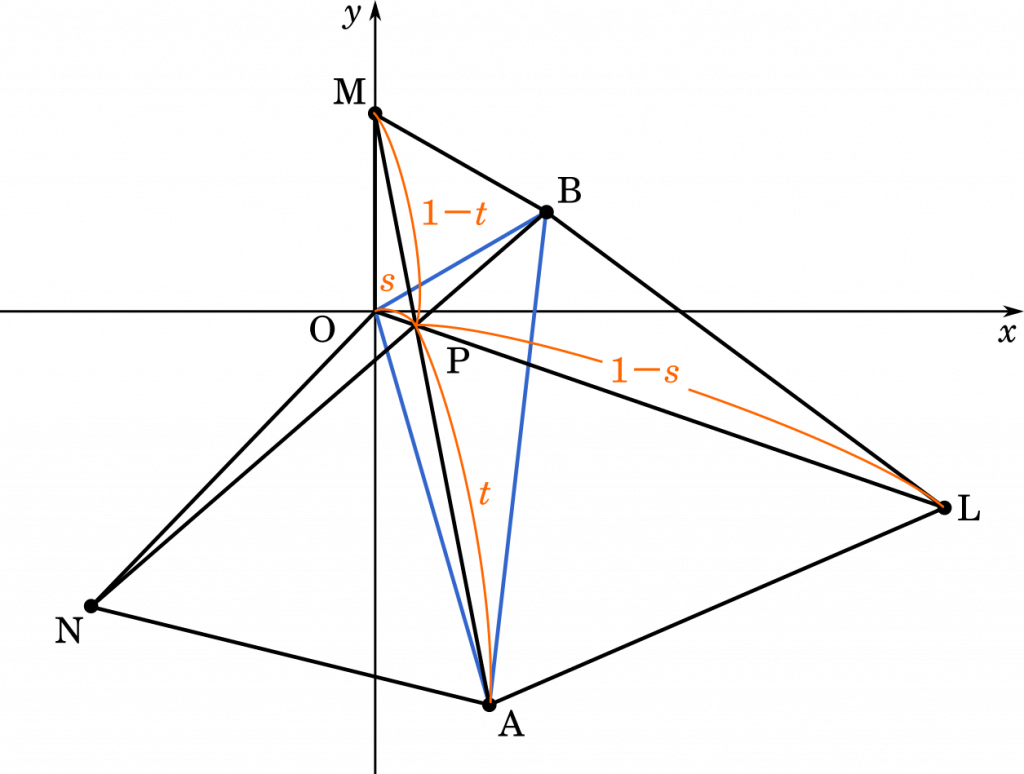
内分点の求め方は，ベクトルで習った方法と同じです。

点 P は辺 OL を $s:1-s$ で内分し，辺 AM を $t:1-t$ で内分すると定めます。

複素数平面でも，内分点の公式はそのまま使えます。

点 P は O と L を $s:1-s$ で内分するので

$(1-s)\cdot0+s(10-2\sqrt{3}i)$

$=10s-2\sqrt{3}si$ ・・・①

点 P は A と M を $t:1-t$ で内分するので

$(1-t)(2-4\sqrt{3}i)+t\cdot2\sqrt{3}i$
$=2-4\sqrt{3}i-2t+4\sqrt{3}ti+2\sqrt{3}ti$
$=2-2t+(6\sqrt{3}t-4\sqrt{3})i$ ・・・②

つまり，①＝②の関係が成り立ちます。

複素数では，実部＝実部，虚部＝虚部の関係が成り立ちます。これを利用して

①と②を比べると

$10s=2-2t$
$5s=1-t$ ・・・③

また

$-2\sqrt{3}s=6\sqrt{3}t-4\sqrt{3}$
$s=2-3t$ ・・・④

④を③に代入すると

$5(2-3t)=1-t$
$10-15t=1-t$
$-14t=-9$
$t=\cfrac{9}{14}$

②に代入すると

$2-2\cdot\cfrac{9}{14}+\Big(6\sqrt{3}\cdot\cfrac{9}{14}-4\sqrt{3}\Big)i$
$=\cfrac{5}{7}+2\sqrt{3}\Big(3\cdot\cfrac{9}{14}-2\Big)i$
$=\cfrac{5}{7}+2\sqrt{3}\Big(-\cfrac{1}{14}\Big)i$
$=\cfrac{5}{7}-\cfrac{\sqrt{3}}{7}i$

したがって

P $\Big(\cfrac{5}{7}-\cfrac{\sqrt{3}}{7}i\Big)$　（答え）

3 点が一直線上であることを示す

(3)に進みます。

$\cfrac{5}{7}-\cfrac{\sqrt{3}}{7}i+5+3\sqrt{3}i=k(3+\sqrt{3}i+5+3\sqrt{3}i)$
$5-\sqrt{3}i+35+21\sqrt{3}i=7k(8+4\sqrt{3}i)$
$40+20\sqrt{3}i=7k(8+4\sqrt{3}i)$
$10+5\sqrt{3}i=7k(2+\sqrt{3}i)$
$7k=\cfrac{10+5\sqrt{3}i}{2+\sqrt{3}i}$
$=\cfrac{(10+5\sqrt{3}i)(2-\sqrt{3}i)}{(2+\sqrt{3}i)(2-\sqrt{3}i)}$
$=\cfrac{20-10\sqrt{3}i+10\sqrt{3}i+15}{4+3}$
$=\cfrac{35}{7}$
$k=\cfrac{5}{7}$

実数 $k$ が存在するので，3 点 B，P，N は一直線上にある。（証明終わり）