【軌跡と領域】2 点からの距離の比が等しい点の軌跡－求め方をおさらい

軌跡が直線になるパターン

[問題1] 2 点 A$(-3,2)$，B$(3,-1)$ に対して，AP：BP＝1：1 を満たす点 P の軌跡を求めよ。

AP：BP＝1：1　より
AP＝BP
が成り立ちます。両辺を 2 乗しておきましょう。

$\text{AP}^2=\text{BP}^2$
点 P の座標を $(x,y)$ とすると，三平方の定理より
$\text{AP}^2=(x+3)^2+(y-2)^2$
$\text{BP}^2=(x-3)^2+(y+1)^2$
よって
$(x+3)^2+(y-2)^2=(x-3)^2+(y+1)^2$

$x^2+6x+9+y^2-4y+4=x^2-6x+9+y^2+2y+1$
$12x-6y+3=0$
$4x-2y+1=0$　（答え）

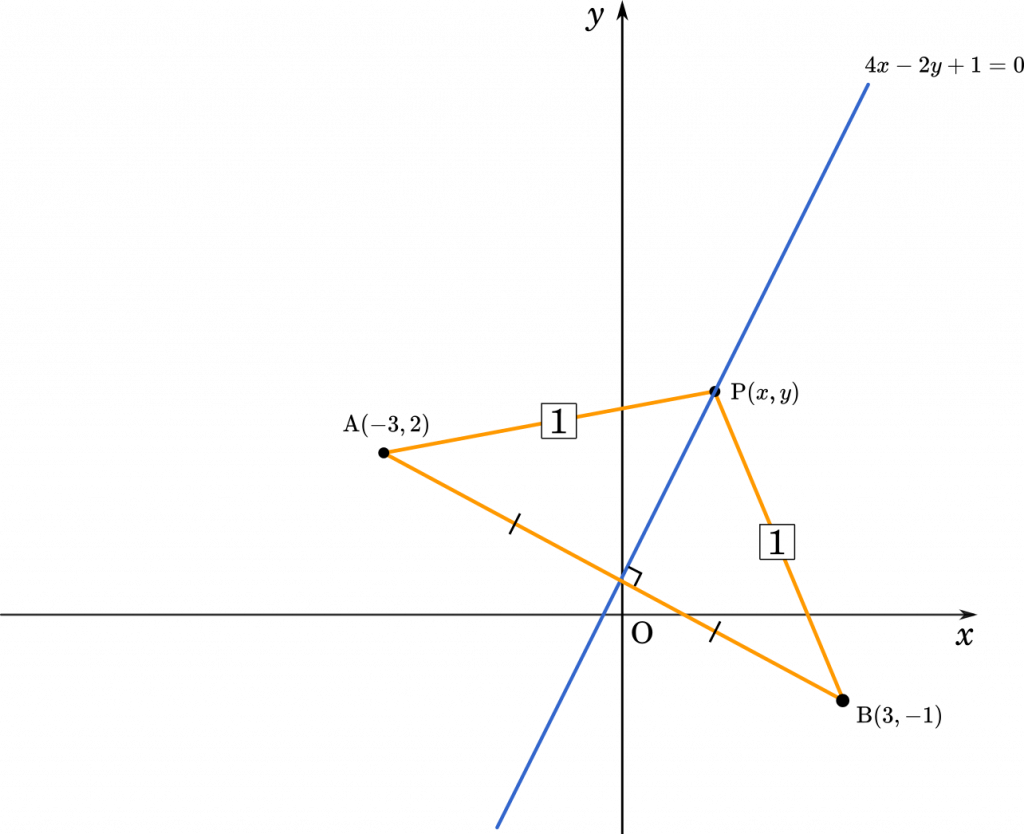
辺の比が 1：1 のときは，このように垂直二等分線ができます。
今度は，辺の比が 1：1 でないときを考えてみましょう。

軌跡が円になるパターン

[問題2] 2 点 A$(-3,2)$，B$(3,-1)$ に対して，AP：BP＝1：2 を満たす点 P の軌跡を求めよ。

$\text{AP}:\text{BP}=1:2$ より
$2\text{AP}=\text{BP}$
両辺を 2 乗して
$4\text{AP}^2=\text{BP}^2$

$\text{AP}^2=(x+3)^2+(y-2)^2$
$\text{BP}^2=(x-3)^2+(y+1)^2$
よって
$4\{(x+3)^2+(y-2)^2\}=(x-3)^2+(y+1)^2$
$4x^2+24x+36+4y^2-16y+16=x^2-6x+9+y^2+2y+1$
$3x^2+30x+3y^2-18y+42=0$
$x^2+10x+y^2-6y+14=0$
$(x+5)^2-25+(y-4)^2-16+14=0$
$(x+5)^2+(y-4)^2=27$
$(x+5)^2+(y-4)^2=(3\sqrt{3})^2$
したがって
点 $(-5,4)$ を中心とする，半径 $3\sqrt{3}$ の円。（答え）

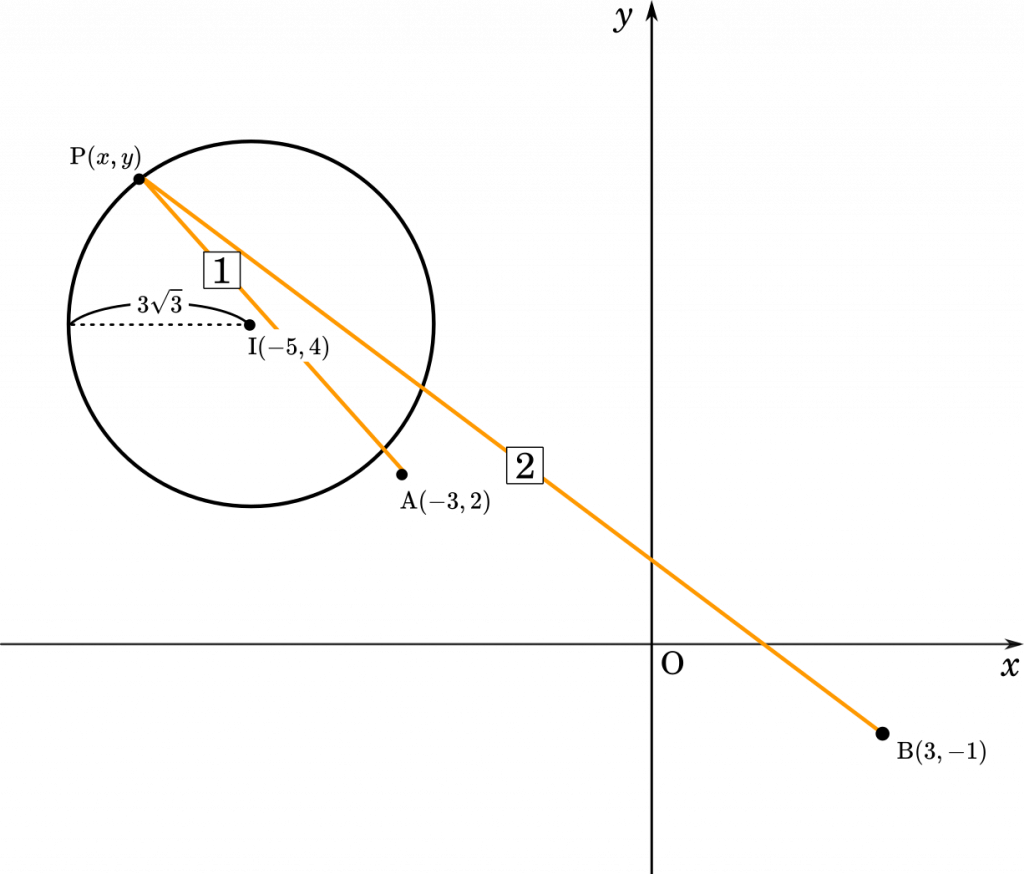
2 つの問題を比べてみると，辺の比が 1：1 のときは $x^2$ と $y^2$ が消えるので，式は直線になります。
一方で，辺の比が 1：1 でないときは $x^2$ と $y^2$ が消去できないので，$x^2$ と $y^2$ の項が含まれる方程式，つまり円になるのです。