【IA】定点を通る二次関数と直線との交点の個数(東京都立大2015文系第4問)

座標平面において曲線 $y=k(1-x^2)-1$ ($k$ は正の定数)を $C_1$ とし，曲線 $y=1-|x|$ を $C_2$ とする。このとき，以下の問いに答えなさい。（東京都立大2015）

(1) $C_1$ は $k$ の値によらない定点を通る。この定点の座標をすべて求めなさい。

(2) $C_1$ と $C_2$ が共有点をもつような正の定数 $k$ の値の範囲を求めなさい。

(3) 正の定数 $k$ が(2)で求めた範囲になるとき，$C_1$ と $C_2$ の共有点の個数を求めなさい。

k が消える場合を考える

(1)から始めます。

$k$ の値によらないということは，式から $k$ の値が消えるということと同じだと考えましょう。

式の形から，$1-x^2$ が 0 になれば，$k\times0$ となって，$k$ が消えます。

つまり

$1-x^2=0$
$x^2=1$
$x=\pm1$

このとき，$k(1-x^2)$ は 0 になるので，どちらも $y=-1$ となります。

したがって

$(1,-1),\space(-1,-1)$　（答え）

判別式を作る

(2)に進みます。

交点を求めるので，式を連立します。ただし，式に絶対値があるので，$x$ が正の場合と負の場合に分けて考えましょう。

(i) $x\geqq0$ のとき

式を連立して

$k(1-x^2)-1=1-x$
$k-kx^2-1=1-x$
$kx^2-x+2-k=0$

共有点を持つということは，判別式が 0 以上と考えることができます。この辺りもセオリーとして覚えましょう。

$D=(-1)^2-4k(2-k)\geqq0$
$1-8k+4k^2\geqq0$

$4k^2-8k+1=0$ とすると

$k=\cfrac{4\pm\sqrt{16-4}}{4}$
$=\cfrac{4\pm2\sqrt{3}}{4}$
$=\cfrac{2\pm\sqrt{3}}{2}$
$k\leqq\cfrac{2-\sqrt{3}}{2}$，$\cfrac{2+\sqrt{3}}{2}\leqq k$

(ii) $x<0$ のとき

$k(1-x^2)-1=1+x$
$k-kx^2-1=1+x$
$kx^2+x+2-k=0$
$D=1-4k(2-k)\geqq0$

(i)と同じ式になったので，$k$ の範囲も同じです。

$k\leqq\cfrac{2-\sqrt{3}}{2}$，$\cfrac{2+\sqrt{3}}{2}\leqq k$

最後に，$k$ は正の定数であることに注意して

$0<k\leqq\cfrac{2-\sqrt{3}}{2}$，$\cfrac{2+\sqrt{3}}{2}\leqq k$

（答え）

共有点の個数を考える

(3)に進みます。

ここは実際にグラフを描いて考えると，理解しやすいでしょう。

(i) $k=\cfrac{2-\sqrt{3}}{2}$ のとき

まず，$D=0$ の場合から考えると良いでしょう。

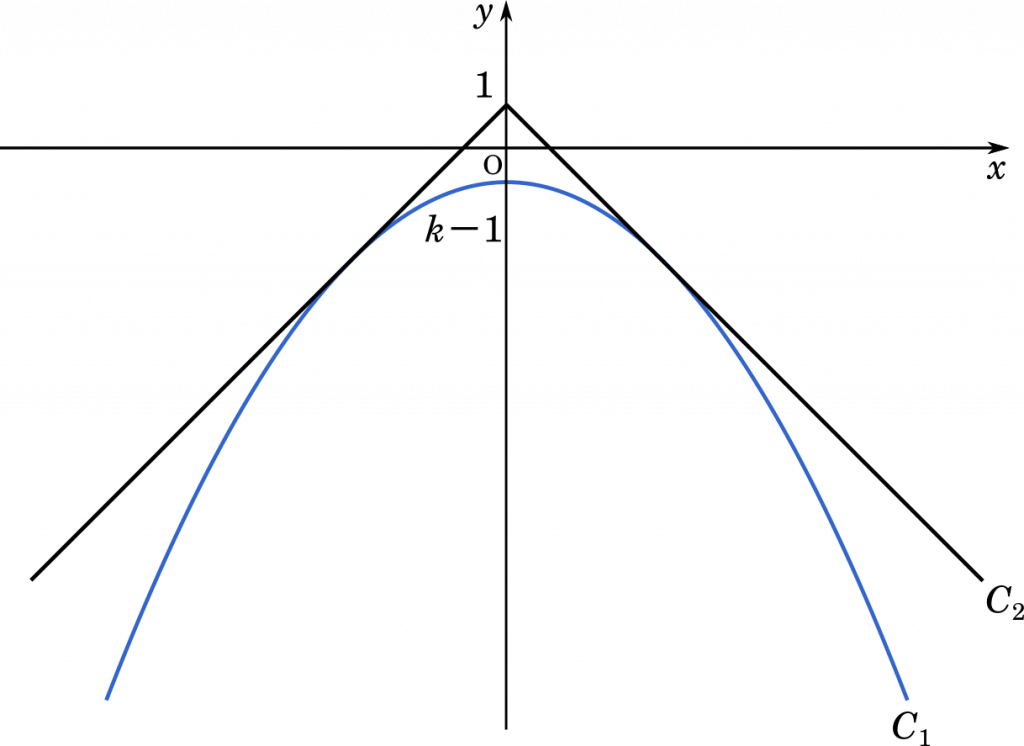
また，$k=\cfrac{2+\sqrt{3}}{2}$ のときも $D=0$ となるので，共有点は 2 個です。

(ii) $0<k<\cfrac{2-\sqrt{3}}{2}$ のとき

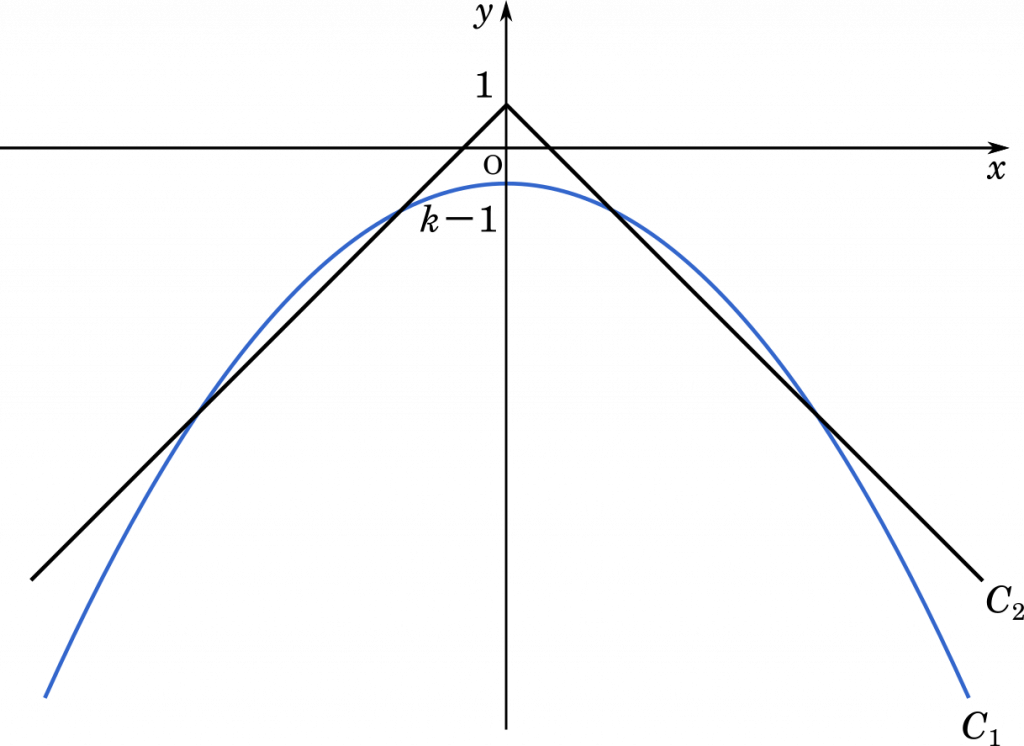
判別式としては $D>0$ だから，共有点は 2 個ですが，上と同様に $x\geqq0$ のときと，$x<0$ のときで 2 個ずつできます。合わせて 4 個です。

また，判別式から考えて，$\cfrac{2+\sqrt{3}}{2}<k$ のときも共有点は 4 個できます。ただし，これには注意が必要です。

(iii) $k=2$ のとき

$C_1$ と $y$ 軸との交点は $k-1$ であり，$k=2$ のとき，$k-1=1$ となります。これは $C_2$ 上の点でもあります。

(iv) $k>2$ のとき

さらに注意が必要な場合が，$k>2$ のときです。

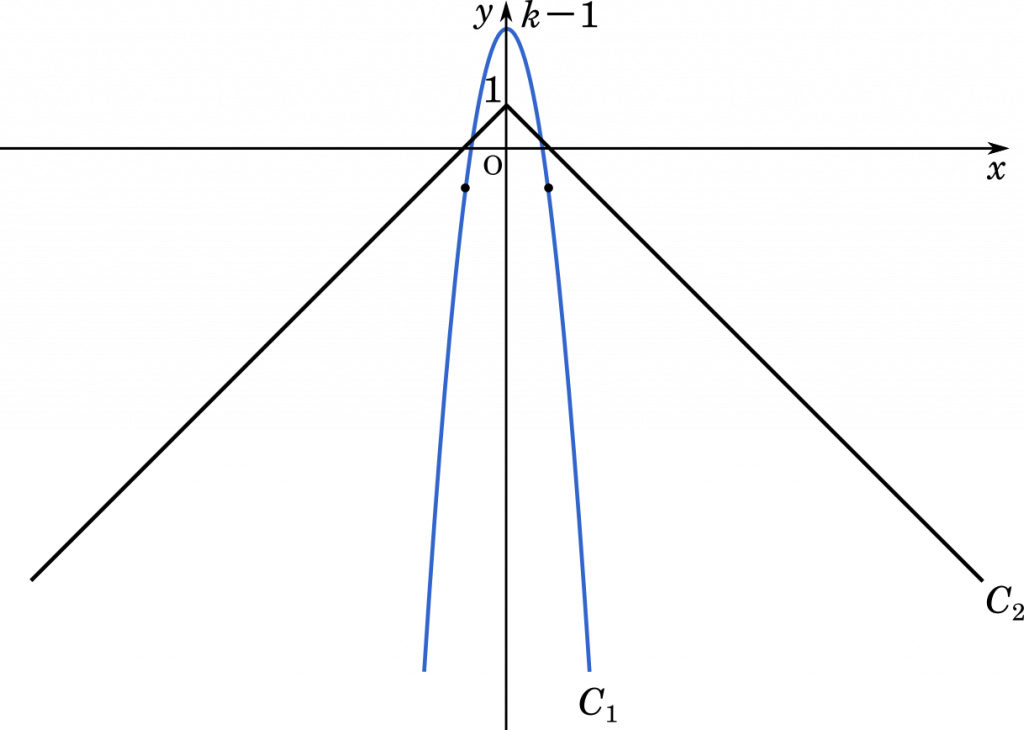
したがって

$0<k<\cfrac{2-\sqrt{3}}{2}$ のとき 4 個。
$k=\cfrac{2\pm\sqrt{3}}{2}$ のとき 2個。
$\cfrac{2+\sqrt{3}}{2}<k<2$ のとき 4 個。
$k=2$ のとき 3 個。
$k>2$ のとき 2 個。

（答え）

2 次関数のグラフが $y$ 軸上の $k-1$ を通ることと，$(1,-1),\space(-1,-1)$ を通ることに注意して，どのような曲線ができるかを細かく調べていきましょう。