【IIB三角関数】定数分離－三角関数だと当てはまる実数解の個数もいろいろ(東京都立大2015理系第2問)

関数

$f(x)=\sqrt{2}\sin x-\sqrt{2}\cos x-\sin 2x$

に対して，以下の問いに答えなさい。（東京都立大2015）

(1) $t=\cos\Big(x+\cfrac{\pi}{4}\Big)$ とおくとき，$f(x)$ を $t$ の式で表しなさい。

(2) $f(x)$ の最大値と最小値を求めなさい。

(3) 方程式 $f(x)=a$ が $0\leqq x<2\pi$ の範囲で相異なる 2 つの解をもつための実数 $a$ の条件を求めなさい。

加法定理と2倍角の公式

(1)から始めます。

$t=\cos\Big(x+\cfrac{\pi}{4}\Big)$

加法定理で $x+\cfrac{\pi}{4}$ の部分を分解しましょう。

$=\cos x\cos\cfrac{\pi}{4}-\sin x\sin\cfrac{\pi}{4}$
$=\cfrac{\sqrt{2}}{2}\cos x-\cfrac{\sqrt{2}}{2}\sin x$

よって

$2t=\sqrt{2}\cos x-\sqrt{2}\sin x$ ・・・①

次に，①を 2 乗すると良いでしょう。

$2t=\sqrt{2}(\cos x-\sin x)$
$4t^2=2(\cos^2x-2\sin x\cos x+\sin^2 x)$
$=2(1-2\sin x\cos x)$

よって

$=2(1-\sin 2x)$
$=2-2\sin 2x$
$2\sin2x=2-4t^2$
$\sin2x=1-2t^2$　・・・②

①，②は符号を逆にして

$-2t=\sqrt{2}\sin x-\sqrt{2}\cos x$ ・・・①’
$-\sin2x=2t^2-1$ ・・・②’

①’，②’を $f(x)$ に代入すると

$f(x)=2t^2-2t-1$　（答え）

関数の最大・最小

$g(t)=2t^2-2t-1$ として，平方完成します。

$=2\Big(t-\cfrac{1}{2}\Big)^2-\cfrac{1}{2}-1$
$=2\Big(t-\cfrac{1}{2}\Big)^2-\cfrac{3}{2}$

また，$t=\cos\Big(x+\cfrac{\pi}{4}\Big)$ だから，範囲が存在します。

$-1\leqq\cos\Big(x+\cfrac{\pi}{4}\Big)\leqq1$
$-1\leqq t\leqq1$

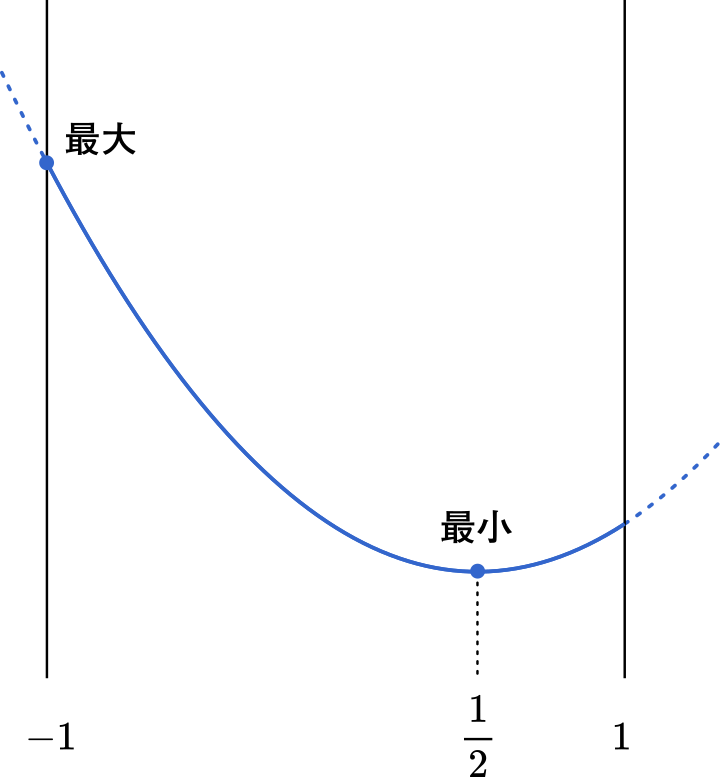
図を描いてみると，最大値は $t=-1$ のときで，最小値は $t=\cfrac{1}{2}$ のときであることが分かります。

$f(-1)=2(-1)^2-2(-1)-1=3$

また，$t=-1$ のとき

$\cos\Big(x+\cfrac{\pi}{4}\Big)=-1$
$x+\cfrac{\pi}{4}=\pi$
$x=\cfrac{3\pi}{4}$

$f\Big(\cfrac{1}{2}\Big)=-\cfrac{3}{2}$

また，$t=\cfrac{1}{2}$ のとき

$\cos\Big(x+\cfrac{\pi}{4}\Big)=\cfrac{1}{2}$
$x+\cfrac{\pi}{4}=\cfrac{\pi}{3},\space\cfrac{5\pi}{3}$
$x=\cfrac{\pi}{12},\space\cfrac{17\pi}{12}$

したがって，

最大値は $x=\cfrac{3\pi}{4}+2n\pi$ のとき $3$
最小値は $x=\cfrac{\pi}{12}+2n\pi,\space\cfrac{17\pi}{12}+2n\pi$ のとき $-\cfrac{3}{2}$
（$n$ は整数）

（答え）

あてはまる cos が 1 個のときと 2 個のときを仕分けする

(3)に進みます。

$f(x)=a$　より
$2t^2-2t-1=a$ として

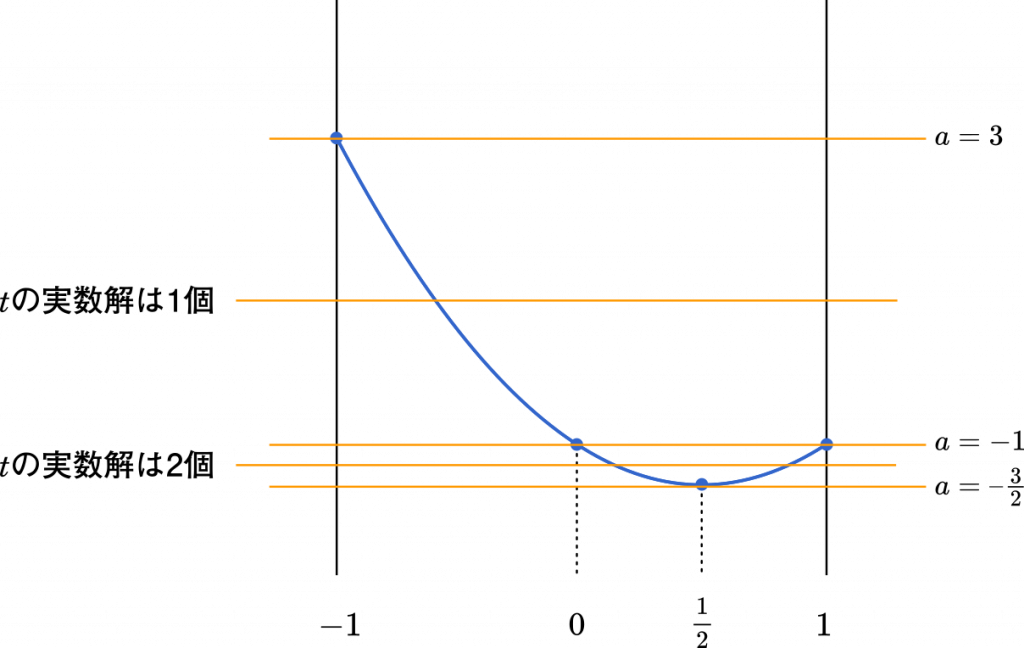
$a=-\cfrac{3}{2}$ のとき，$t$ は 1 個の実数解を持ちます。

(2)でやったように，このとき当てはまる $x$ は $\cfrac{\pi}{12},\space\cfrac{17\pi}{12}$ の 2 個があるので，問題文の条件に当てはまります。

次に $t=1$ の点について考えましょう。$g(t)$ に $t=1$ を代入して

$2\cdot1^2-2\cdot1-1=-1$

これをグラフに書いてみると，$-1\leqq a\leqq3$ の範囲で $t$ の実数解が 1 個になり，それに当てはまる $x$ は 2 個あるので，問題文の条件を満たします。

実は，上の不等式は正しくありません。こうした問題を考えるときには，範囲の端点に注意する必要があります。

まず，$a=-1$ のとき，$t$ の実数解は $t=0,1$ の 2 個になるはずです。このとき

$\cos\Big(x+\cfrac{\pi}{4}\Big)=0$
$x+\cfrac{\pi}{4}=\cfrac{\pi}{2},\space\cfrac{3\pi}{2}$
$x=\cfrac{\pi}{4},\cfrac{5\pi}{4}$

となり，当てはまる $x$ は 2 個です。また

$\cos\Big(x+\cfrac{\pi}{4}\Big)=1$
$x+\cfrac{\pi}{4}=0$
$x=-\cfrac{\pi}{4}=\cfrac{7\pi}{4}$

となり，当てはまる $x$ は 1 個です。

つまり，$a=-1$ のとき，$x$ の実数解は 3 個あります。

次に，$t=-1$ として

$\cos\Big(x+\cfrac{\pi}{4}\Big)=-1$
$x+\cfrac{\pi}{4}=\pi$
$x=\cfrac{3\pi}{4}$

となり，$x$ の実数解は 1 個だけです。

こうして，正しい不等式は

$-1<a<3$

となります。

したがって，実数 $a$ の条件は

$a=-\cfrac{1}{2}$，$-1<a<3$ （答え）