【数III微積】1/(3+x^3) の積分は tan で置換する（国公立レベル）(東京都立大2015理系第3問)

座標平面において曲線 $y=\cfrac{3}{x^2+3}$ を $C_1$，曲線 $y=x^2+k$ （$k$ は定数）を $C_2$ とする。$C_1$ と $C_2$ のすべての共有点において互いの接線が直交しているとき，以下の問いに答えなさい。（東京都立大2015）

(1) 定数 $k$ の値を求めなさい。また，$C_1$ と $C_2$ のすべての共有点の座標を求めなさい。

(2) $C_1$ と $C_2$ で囲まれる部分の面積 $S$ を求めなさい。

直線どうしが直交するとき

共有点を見つけようとすると

$\cfrac{3}{x^2+3}=x^2+k$
$(x^2+3)(x^2+k)=3$
$x^4+(3+k)x^2+3k=3$
$x^4+(3+k)x^2+3k-3=0$
$x^2=\cfrac{-3-k\pm\sqrt{9+6k+k^2-12k+12}}{2}$
$=\cfrac{-3-k\pm\sqrt{k^2-6k+21}}{2}$

共有点から見つけるのはどうも難しいようです。そこで，もう一つの条件，接線が直交するところから攻めてみましょう。

式を微分して接線の傾きを求めます。

$C_1:y=\cfrac{3}{x^2+3}$

$y’=\cfrac{(3)'(x^2+3)-3(x^2+3)’}{(x^2+3)^2}$
$=-\cfrac{6x}{(x^2+3)^2}$　・・・①

$C_2:y=x^2+k$
$y’=2x$　・・・②

①，②より

$-\cfrac{6x}{(x^2+3)^2}\cdot2x=-1$

$12x^2=(x^2+3)^2$
$12x^2=x^4+6x^2-9$
$x^4-6x^2+9=0$
$(x^2-3)^2=0$
$x^2=3$
$x=\pm\sqrt{3}$

$\sqrt{3}$，$-\sqrt{3}$ のどちらでも良いのですが，共有点の式に代入しましょう。

$\cfrac{3}{(\sqrt{3})^2+3}=(\sqrt{3})^2+k$
$\cfrac{1}{2}=3+k$
$k=-\cfrac{5}{2}$　（答え）

つまり，$k=-\cfrac{5}{2}$ の条件において，すべての共有点で互いの接線が直交していることになります。このとき $x=\pm\sqrt{3}$ だから，$C_2$ に代入して

$(\sqrt{3})^2-\cfrac{5}{2}=3-\cfrac{5}{2}$
$=\cfrac{1}{2}$

同様に

$(-\sqrt{3})^2-\cfrac{5}{2}=\cfrac{1}{2}$

したがって，共有点は

$\Big(\sqrt{3},\space\cfrac{1}{2}\Big),\space\Big(-\sqrt{3},\space\cfrac{1}{2}\Big)$　（答え）

tan の置換積分

(2)に進みます。

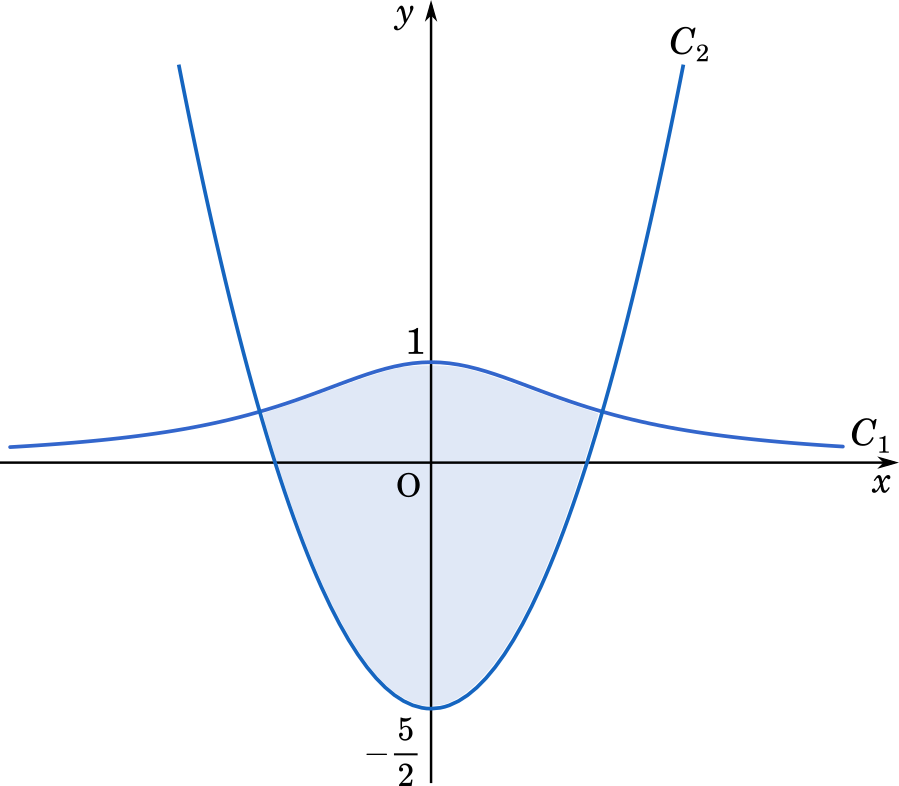
$\displaystyle S=\int_{-\sqrt{3}}^{\sqrt{3}}\cfrac{3}{x^2+3}-x^2+\cfrac{5}{2}\space dx$

さらに，$y=\cfrac{3}{x^2+3}$ は，例えば  $x$ に $1$ を代入したときと $-1$ を代入したときでどちらも $\cfrac{3}{4}$ になるので，それをもとに遇関数であることに気づくと良いでしょう。

よって

$\displaystyle S=2\int_0^{\sqrt{3}}\cfrac{3}{x^2+3}-x^2+\cfrac{5}{2}\space dx$

ここで

$\displaystyle\int_0^{\sqrt{3}}\cfrac{3}{x^2+3}\space dx$

分母に数字＋$x^2$ の形がきたら，$\tan$ に置換するとうまくいきます。

$x=\sqrt{3}\tan\theta$ とおくと

$dx=\cfrac{\sqrt{3}}{\cos^2\theta}\space d\theta$

$\def\arraystretch{1.5}\begin{array}{|c|c|c|}\hline x&0&\sqrt{3}\\\hline\theta&0&\frac{\pi}{4}\\\hline\end{array}$

式を $\theta$ に置き変えていきましょう。

$\displaystyle\int_0^{\small{\frac{\pi}{4}}}\cfrac{3}{(\sqrt{3}\tan\theta)^2+3}\cdot\cfrac{\sqrt{3}}{\cos^2\theta}\space d\theta$
$\displaystyle=\int_0^{\small{\frac{\pi}{4}}}\cfrac{3}{3\tan^2\theta+3}\cdot\cfrac{\sqrt{3}}{\cos^2\theta}\space d\theta$
$\displaystyle=\int_0^{\small{\frac{\pi}{4}}}\cfrac{3}{3(1+\tan^2\theta)}\cdot\cfrac{\sqrt{3}}{\cos^2\theta}\space d\theta$
$\displaystyle=\int_0^{\small{\frac{\pi}{4}}}\cfrac{1}{1+\tan^2\theta}\cdot\cfrac{\sqrt{3}}{\cos^2\theta}\space d\theta$

$\displaystyle=\int_0^{\small{\frac{\pi}{4}}}\cfrac{1}{\cfrac{1}{\cos^2\theta}}\cdot\cfrac{\sqrt{3}}{\cos^2\theta}\space d\theta$
$\displaystyle=\int_0^{\small{\frac{\pi}{4}}}\sqrt{3}\space d\theta$
$=\Big[\sqrt{3}\theta\Big]_0^{\small{\frac{\pi}{4}}}$
$=\cfrac{\sqrt{3}\pi}{4}$

また

$\displaystyle\int_0^{\sqrt{3}}-x^2+\cfrac{5}{2}\space dx$
$=\Big[-\cfrac{x^3}{3}+\cfrac{5}{2}x\Big]_0^{\sqrt{3}}$
$=-\sqrt{3}+\cfrac{5\sqrt{3}}{2}$
$=\cfrac{3\sqrt{3}}{2}$

したがって

$S=2\Big(\cfrac{\sqrt{3}\pi}{4}+\cfrac{3\sqrt{3}}{2}\Big)$
$=\cfrac{\sqrt{3}\pi}{2}+3\sqrt{3}$　（答え）