a を実数とする。関数 f(x) を
f(x)=41(log21x2)2−log21(8x1−a)+a−8 (1≦ x≦4)
と定める。t=log21x とおくとき,以下の問いに答えなさい。
(1) f(x) を t を用いて表しなさい。
(2) 1≦ x≦4 のとき,t の値の範囲を求めなさい。
(3) 次の条件(*)をみたす a の値の範囲を求めなさい。
(*)1≦ x≦4 のとき,f(x)<0 である。
対数関数の整理
(1)から始めます。
f(x)=41(2log21x)2−(log218+log21x1−a)+a−8
ここ,
log21(8x1−a)=(1−a)log218x ってしたらダメですか?
もし,式が
log21(8x)1−a だったら,
=(1−a)log218x になるよ。違いをよく見て。
次に,log218 の値を考えてみましょう。これは,21 を何乗したら 8 になる?ということです。
マイナス使って。
(21)−1=2 になるから,
(21)−3=8 になる。
よって
=41(2t)2−{−3+(1−a)log21x}+a−8
=t2+3−(1−a)t+a−8
=t2−(1−a)t+a−5 (答え)
t の範囲を求める
(2)に進みます。
log211=0
log214=−2
したがって
−2≦ t≦0 (答え)
値が負になる場合を考える
(3)に進みます。
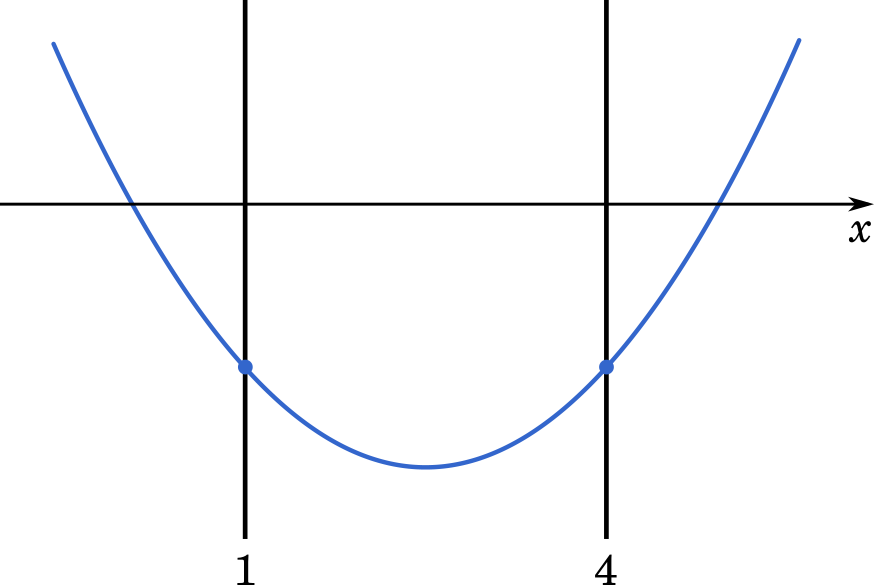
f(x) は下に凸のグラフなので,f(1)<0 かつ f(4)<0 であれば,1≦ x≦4 の区間において,f(x) はつねに負の値であると言えます。
(1) より f(x)=t2−(1−a)t+a−5 とする。
(2)より,x=1 のとき t=0 だから
f(1)=a−5<0
a<5
また
x=4 のとき t=−2 だから
f(4)=(−2)2−(1−a)(−2)+a−5
=4+2−2a+a−5
=−a+1
−a+1<0
a>1
したがって
1<a<5 (答え)
関連