【数Ⅲ積分】sin×cos の積分が解けない　積を和に直して解決

sin の加法定理から積ー和に変換

$\displaystyle\int \sin 2x\cos x dx$

$\displaystyle\int\sin 2x(\sin x)’dx\\\displaystyle=\sin 2x\sin x-\int2\cos 2x\sin x dx$

$\sin(2x+x)=\sin2x\cos x+\cos 2x\sin x$

このようにして、$\sin 2x\cos x$ の形をいったん作ります。しかし、これでは $\cos 2x\sin x$ の部分がジャマです。

$\sin(2x+x)=\sin2x\cos x+\cos 2x\sin x\cdots\text{①}\\\sin(2x-x)=\sin2x\cos x-\cos 2x\sin x\cdots\text{②}$

①＋② より

$\sin(2x+x)+\sin(2x-x)=2\sin 2x\cos x\\\displaystyle\frac{1}{2}\{\sin 3x+\sin x\}=\sin 2x\cos x$

あとは、もとの式を置きかえて計算していきます。

$\displaystyle\int\sin 2x\sin xdx\\\displaystyle=\frac{1}{2}\int \sin 3x+\sin x\enspace dx\\\displaystyle=\frac{1}{2}\left(-\frac{1}{3}\cos 3x-\cos x\right)+C\\\displaystyle=-\frac{1}{6}\cos 3x-\frac{1}{2}\cos x+C$

cos の加法定理から積ー和に変換

$\displaystyle\int\sin 3x\sin 5xdx$

いったん、$\cos$ の加法定理を作ります。

$\cos(3x+5x)=\cos 3x\cos 5x-\sin 3x\sin5x$

ここでもやはり$\cos 3x\cos 5x$ がジャマなので、式をもう一つ作って消去します。

$\cos(3x+5x)=\cos 3x\cos 5x-\sin 3x\sin5x\cdots\text{①}\\\cos(3x-5x)=\cos 3x\cos 5x+\sin 3x\sin5x\cdots\text{②}$

①－② より

$\cos(3x+5x)-\cos(3x-5x)=-2\sin3x\sin5x\\\displaystyle-\frac{1}{2}\left\{\cos8x-\cos(-2x)\right\}=\sin3x\sin5x$

ここで、$\cos(-2x)=\cos2x$

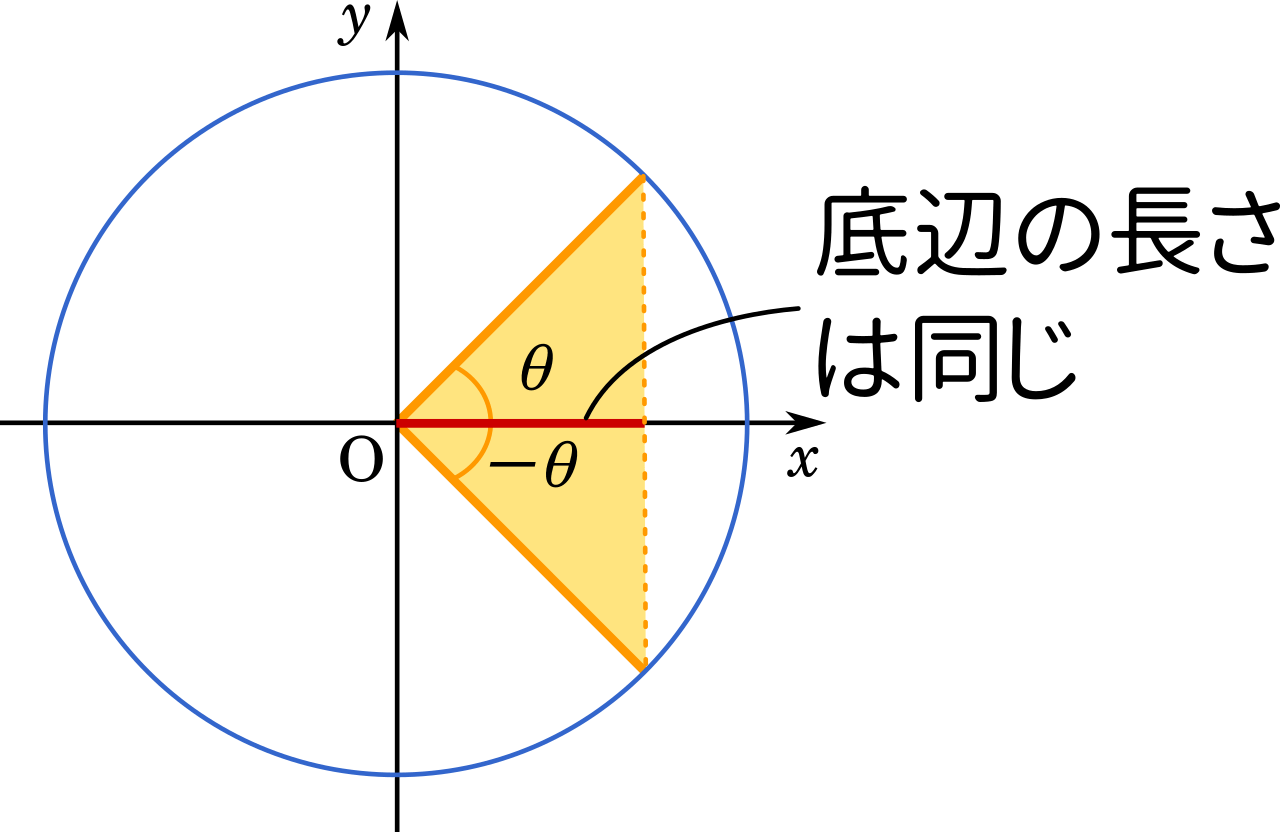
よって、

$\displaystyle-\frac{1}{2}\left\{\cos8x-\cos(-2x)\right\}=\sin3x\sin5x\\\displaystyle-\frac{1}{2}\left\{\cos8x-\cos2x\right\}=\sin3x\sin5x$

これをもとの式に戻すと

$\displaystyle -\frac{1}{2}\int\cos8x-\cos2x\enspace dx\\\displaystyle=-\frac{1}{2}\left(\frac{1}{8}\sin8x-\frac{1}{2}\sin2x\right)+C\\\displaystyle=-\frac{1}{16}\sin8x+\frac{1}{4}\sin2x+C$

(答え)

和積を使うと半角の公式が作れる

かけ算を足し算になおす、が今回の話です。そこで $\sin^2x=\sin x\sin x$ として考えましょう。

$\sin^2x=\sin x\sin x$ より

$\cos(x+x)=\cos x\cos x-\sin x\sin x\cdots\text{①}\\\cos(x-x)=\cos x\cos x+\sin x\sin x\cdots\text{②}$

①－② より

$\cos 2x-\cos 0=-2\sin x\sin x\\\cos 2x-1=-2\sin^2 x\\\displaystyle\sin^2 x=\frac{1-\cos2x}{2}$