【数Ⅲ積分】区分求積の考え方を応用して定積分と不等式を考える

次の(1)、(2)、(3) を示せ。（金沢大）

(1) $\displaystyle \log(n+1)<1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}\enspace (n=1,2,3,\cdots)$
(2) $\displaystyle \lim_{n\rightarrow\infty} \frac{1}{\log n}\sum_{k=1}^n \frac{1}{k}=1$
(3) $\displaystyle \lim_{n\rightarrow\infty}\frac{1}{\log n}\int_1^{n+1} \left|\frac{\sin \pi x}{x}\right|dx=\int_0^1 \sin \pi y\enspace dy=\frac{2}{\pi}$

---

面積の大小で比べていく

(1)から考えていきます。まず、不等式の右側の$\displaystyle 1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$を図にするとこのようになります。

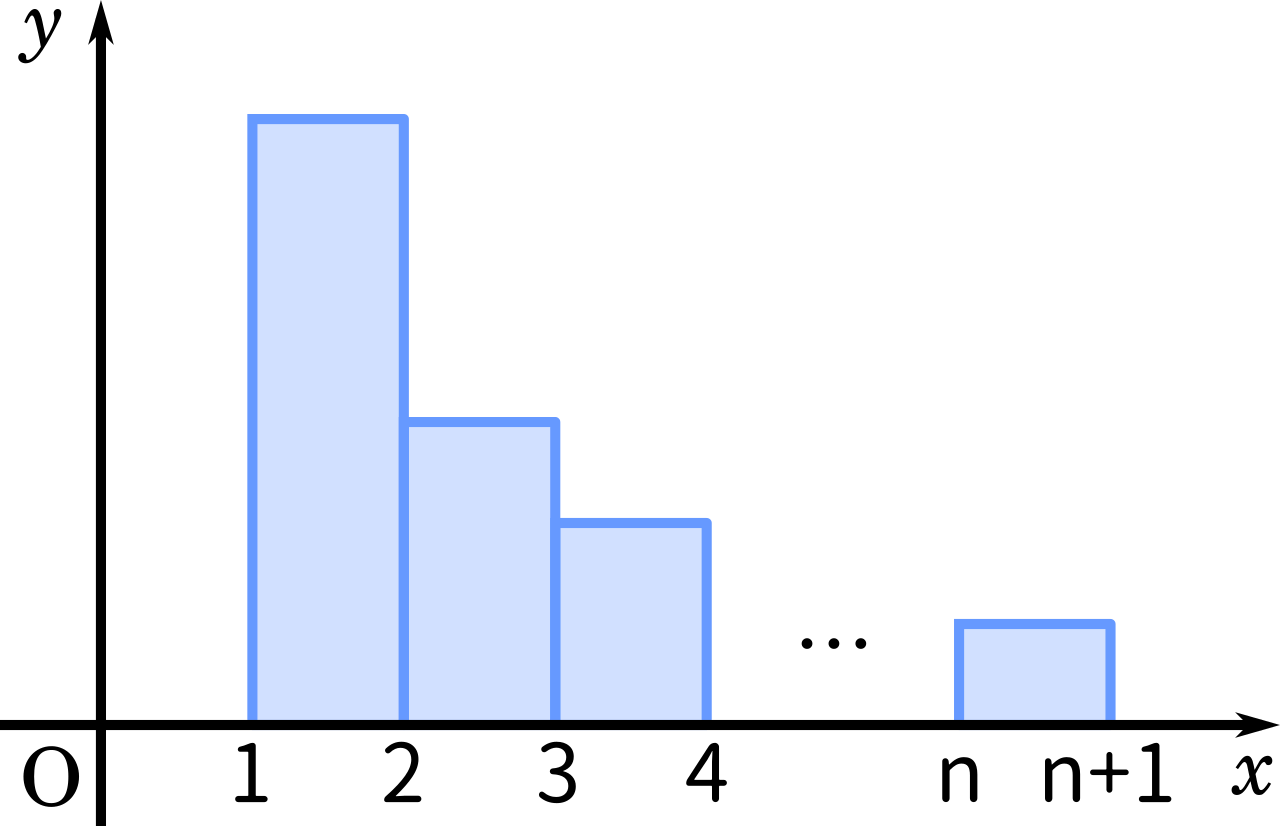
この図を見て、教科書で区分求積を習ったことを思い出しましょう。教科書の例題では $y=x^2$ の積分で習ったと思いますが、今回は $\displaystyle y=\frac{1}{x}$ になっていて、なおかつそれを積分すると $ \log x$ になるので、問題文の式にうまく当てはまりそうです。

上の図の長方形はすべて横の長さが $1$ です。つまり
$\displaystyle 1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$
を
$\displaystyle 1\cdot 1+\frac{1}{2}\cdot 1+\frac{1}{3}\cdot 1+\cdots+\frac{1}{n}\cdot 1$
と考えれば、長方形の面積を足し合わせたものが不等式の右側になります。
次に $\displaystyle \frac{1}{x}$ のグラフと比べていきます。

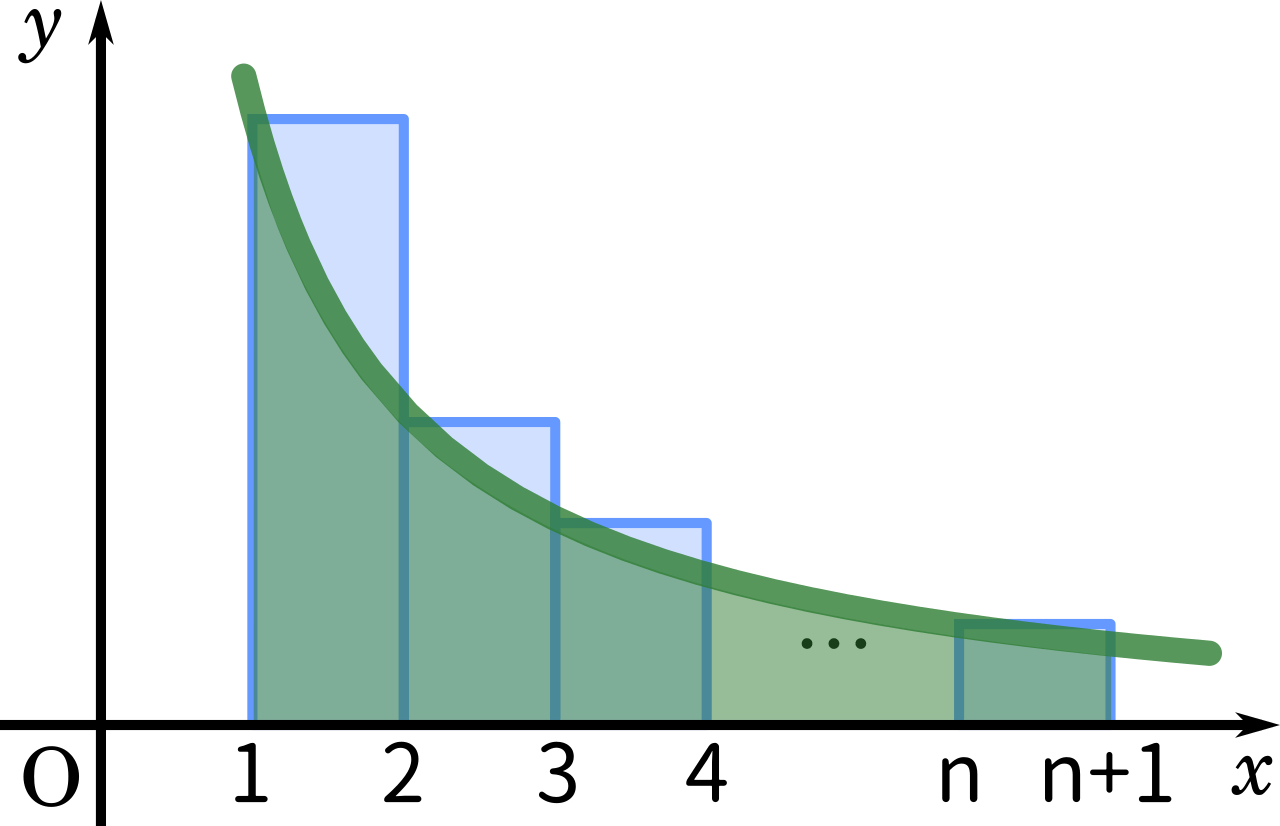
このようにグラフを描いてみると、$\displaystyle \frac{1}{x}$ で囲んだ緑色の部分よりも長方形の面積の合計の方が大きいことが分かります。

また、積分した結果が $\log (n+1)$ であれば問題にぴったり合うので、積分区間を $1$ から $n+1$ で設定してやるとうまくいきそうです。

これを式で表すと
$\displaystyle \int_1^{n+1} \frac{1}{x}\enspace dx<1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$

ここからさらに長方形の作り方を変えてもう一つ図を作ります。

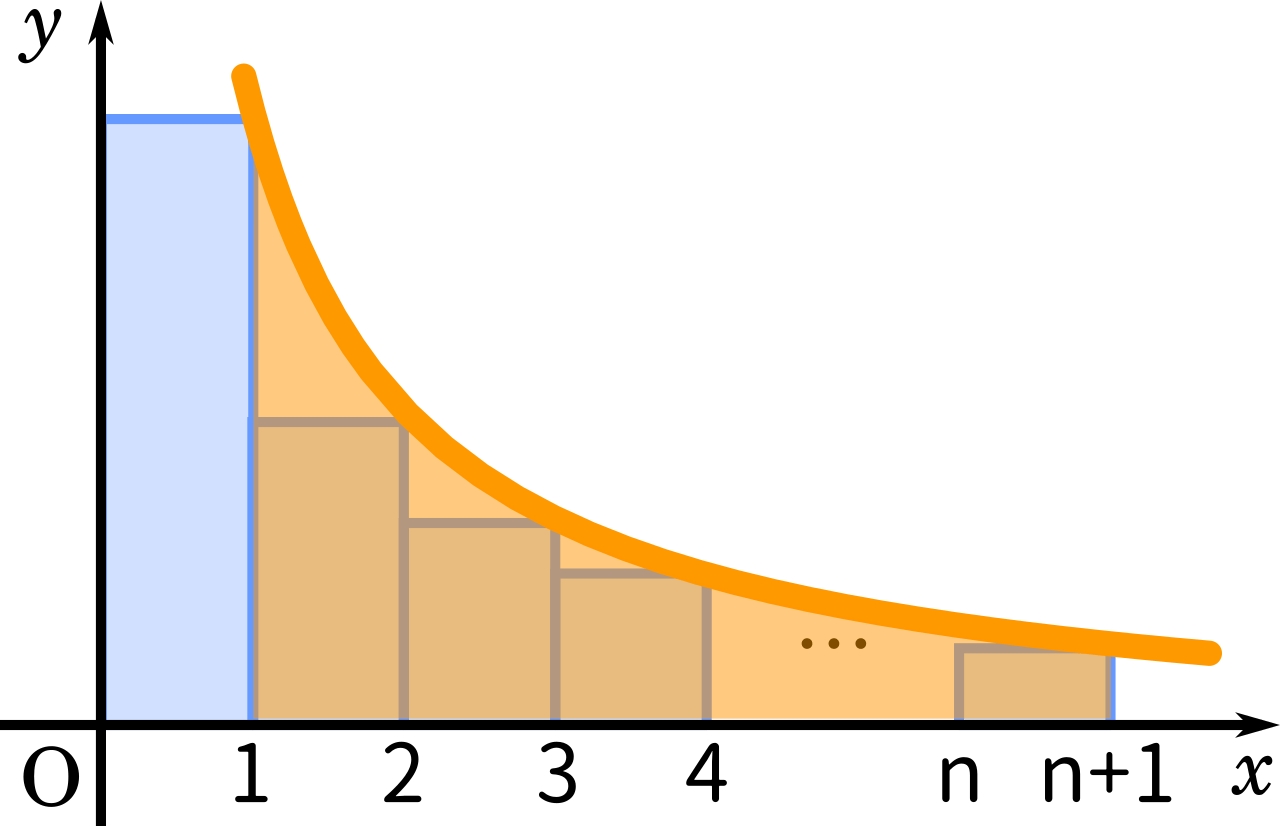
先ほどの図はそれぞれの値から右側に長方形を作りましたが、今度は左側に長方形を作っています。そうすると、長方形の面積の合計より関数のグラフの面積の方が大きくなります。最初の長方形は範囲外であることに注意して式で表すと

$\displaystyle \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{n+1}<\int_1^{n+1} \frac{1}{x}\enspace dx$
となります。

二つの式を合わせると
$\displaystyle \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{n+1}<\int_1^{n+1} \frac{1}{x}\enspace dx<1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$
ここで
$\displaystyle \int_1^{n+1} \frac{1}{x}\enspace dx\\\displaystyle=\left[\log x\right]_1^{n+1}\\=\log(n+1)-\log 1\\=\log(n+1)-0\\=\log(n+1)$
よって
$\displaystyle \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{n+1}<\log(n+1)<1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$
式の右側より
$\displaystyle \log(n+1)<1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$

（答え）

はさみうちの原理を使う

(2) $\displaystyle \lim_{n\rightarrow\infty} \frac{1}{\log n}\sum_{k=1}^n \frac{1}{k}=1$

ここで
$\displaystyle \sum_{k=1}^n \frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$
だから、(1)で作った式が使えそうです。

いったん(1)の答えを変形してみましょう。
$\displaystyle \log(n+1)<1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}\\\displaystyle \log(n+1)<\sum_{k=1}^n \frac{1}{k}\\\displaystyle\frac{\log(n+1)}{\log n}<\frac{1}{\log n}\sum_{k=1}^n \frac{1}{k}$

右辺は問題文の形になりましたが、困るのは左辺です。左辺を $n\rightarrow\infty$ とすると $\displaystyle \frac{\infty}{\infty}$ となり、いわゆる不定形になってしまいます。

つまずきました。こういう時は(1)で作った式を見て作戦の立て直しです。

$\displaystyle \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{n+1}<\log(n+1)<1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$

$\displaystyle \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{n+1}<\log(n+1)<1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$
より
$\displaystyle \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{n}<\log n<1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n-1}\cdots\text{①}$
ここで問題の初めに戻って思い出すと
$\displaystyle \sum_{k=1}^n \frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$
だったので、式を$\displaystyle 1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$ に合わせてみます。

①の左側を変形すると
$\displaystyle \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{n}<\log n\\\displaystyle 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{n}<1+\log n\\\displaystyle\sum_{k=1}^n\frac{1}{k}=1+\log n$

①の右側を変形すると
$\displaystyle\log n<1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n-1}\\\displaystyle\log n+\frac{1}{n}<1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n-1}+\frac{1}{n}\\\displaystyle\log n+\frac{1}{n}<\sum_{k=1}^n\frac{1}{k}$

２つを合わせると
$\displaystyle \log n+\frac{1}{n}<\sum_{k=1}^n \frac{1}{k}<1+\log n$

$\displaystyle \log n+\frac{1}{n}<\sum_{k=1}^n \frac{1}{k}<1+\log n\\\displaystyle \frac{\log n+\frac{1}{n}}{\log n}<\frac{1}{\log n}\sum_{k=1}^n \frac{1}{k}<\frac{1+\log n}{\log n}\\\displaystyle1+\frac{1}{n\log n}<\frac{1}{\log n}\sum_{k=1}^n \frac{1}{k}<\frac{1}{\log n}+1$

ここで $n\rightarrow\infty$ とすると
$\displaystyle 1<\lim_{n\rightarrow\infty}\frac{1}{\log n}\sum_{k=1}^n\frac{1}{k}<1$
はさみうちの原理より
$\displaystyle \lim_{n\rightarrow\infty} \frac{1}{\log n}\sum_{k=1}^n \frac{1}{k}=1$

（答え）

サインの山を比べる

(3) $\displaystyle \lim_{n\rightarrow\infty}\frac{1}{\log n}\int_1^{n+1} \left|\frac{\sin \pi x}{x}\right|dx=\int_0^1 \sin \pi y\enspace dy=\frac{2}{\pi}$

まず、$\displaystyle\frac{\sin \pi x}{x}$ のグラフはこうなります。

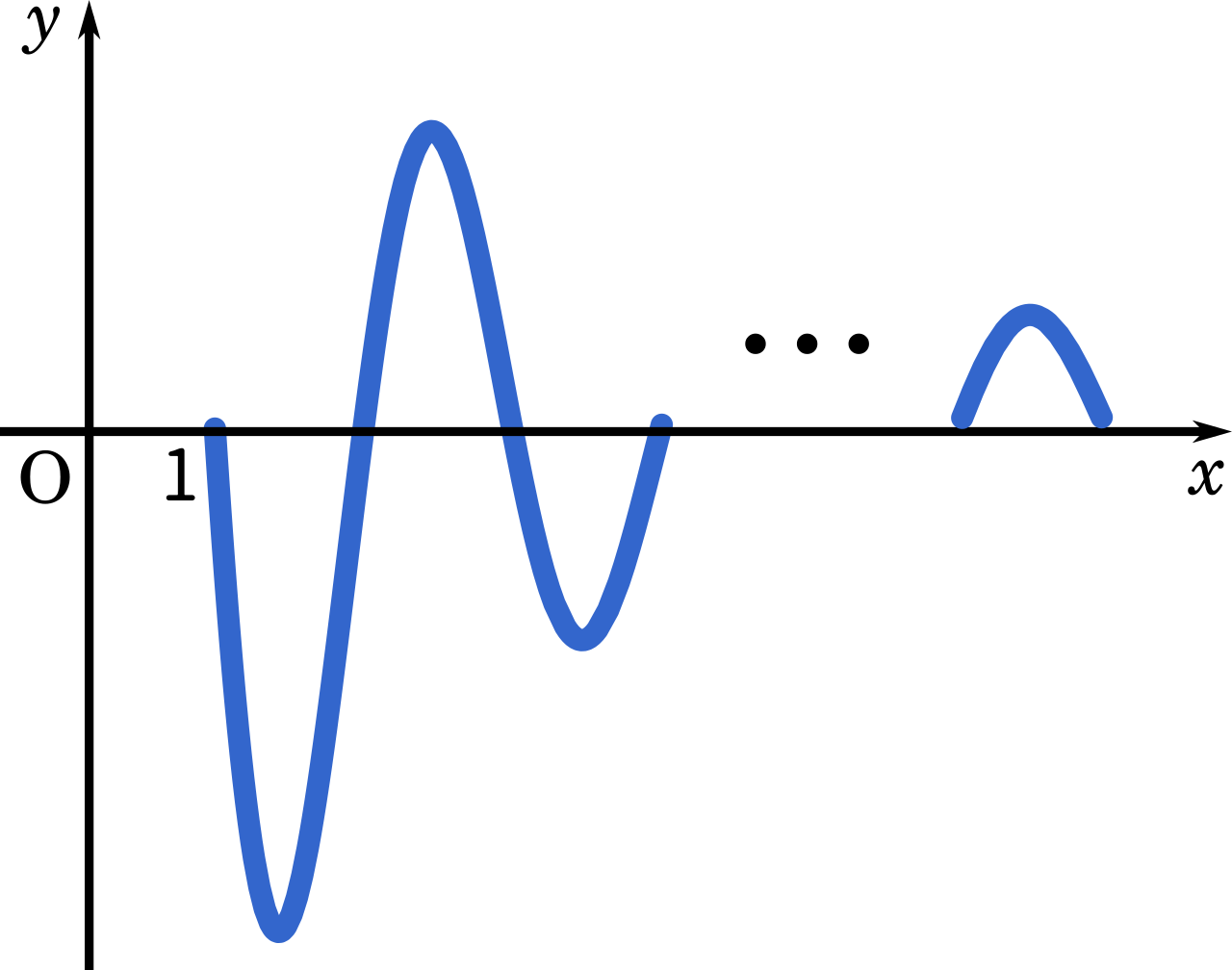
さらに絶対値がつくと

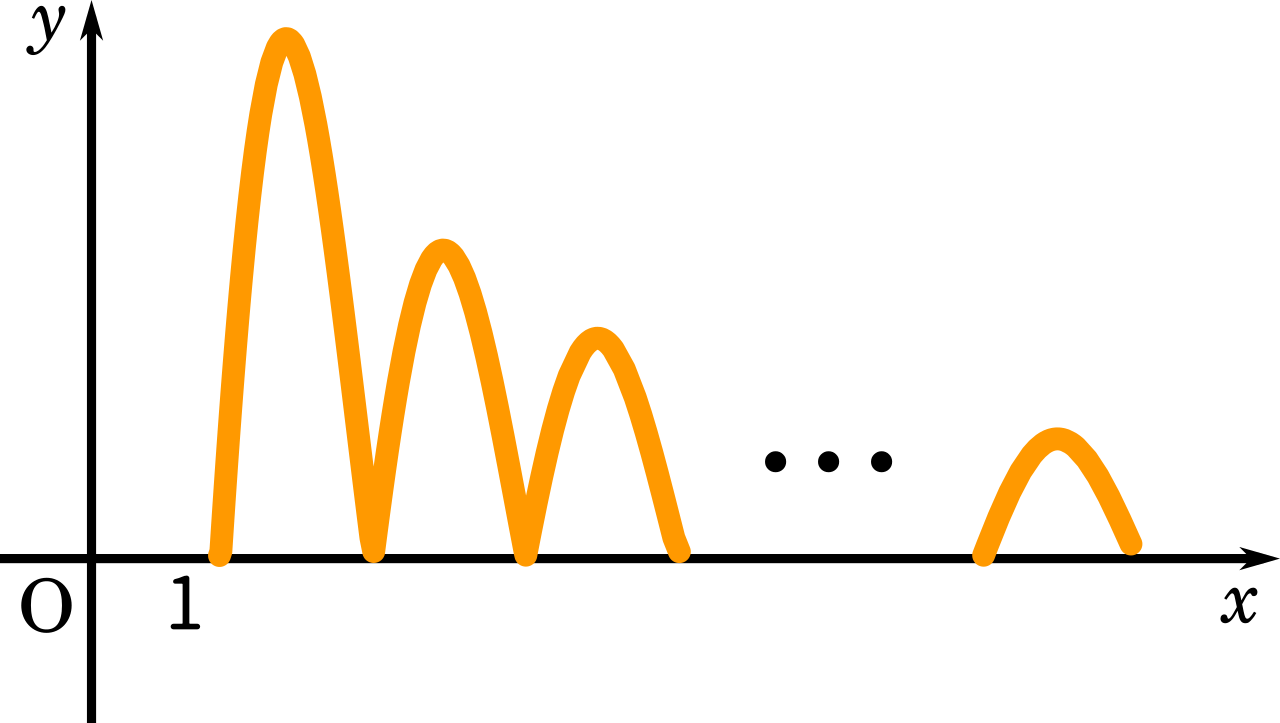
今度は、$\displaystyle\int_0^1 \sin \pi y\enspace dy$ について考えてみます。書き方が少し紛らわしいですが、横軸を $y$ とするとグラフはこうなります。

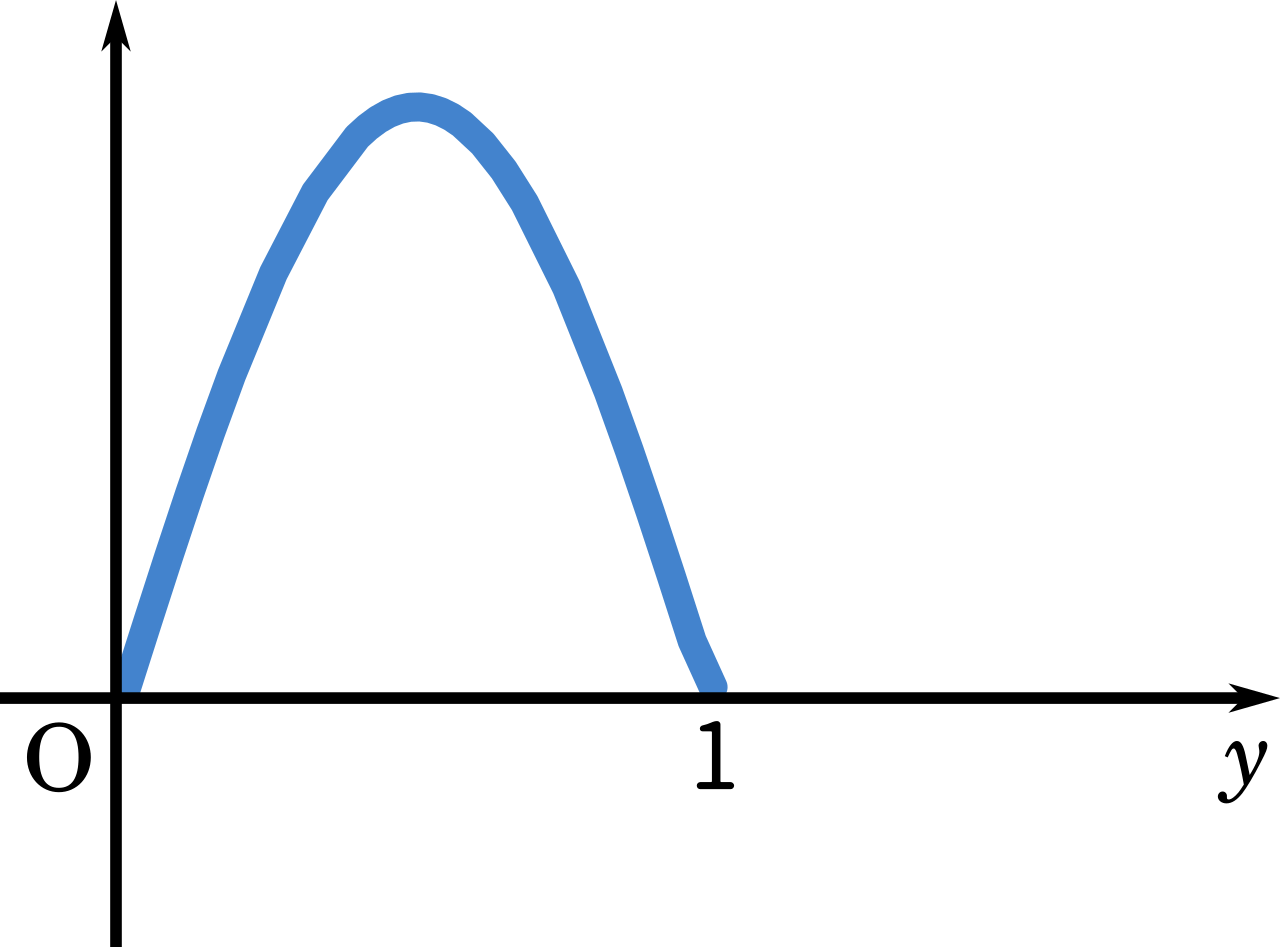
$\displaystyle\int_1^{n+1}|\sin \pi x|\enspace dx$ のグラフは

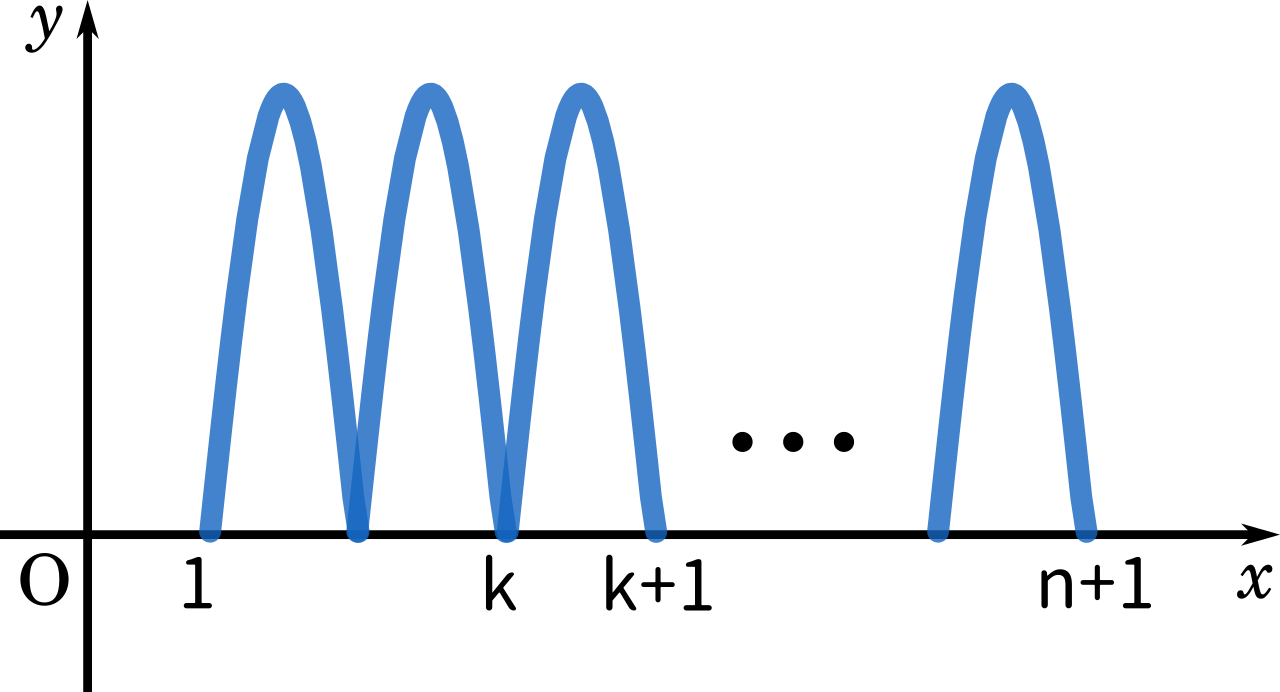
ここで山1つ分を $k$ を使って表すと
$\displaystyle\int_k^{k+1}|\sin \pi x|\enspace dx$
となり
$\displaystyle\int_k^{k+1}|\sin \pi x|\enspace dx=\int_0^1 \sin \pi y\enspace dy\cdots\text{②}$

が成り立ちます。

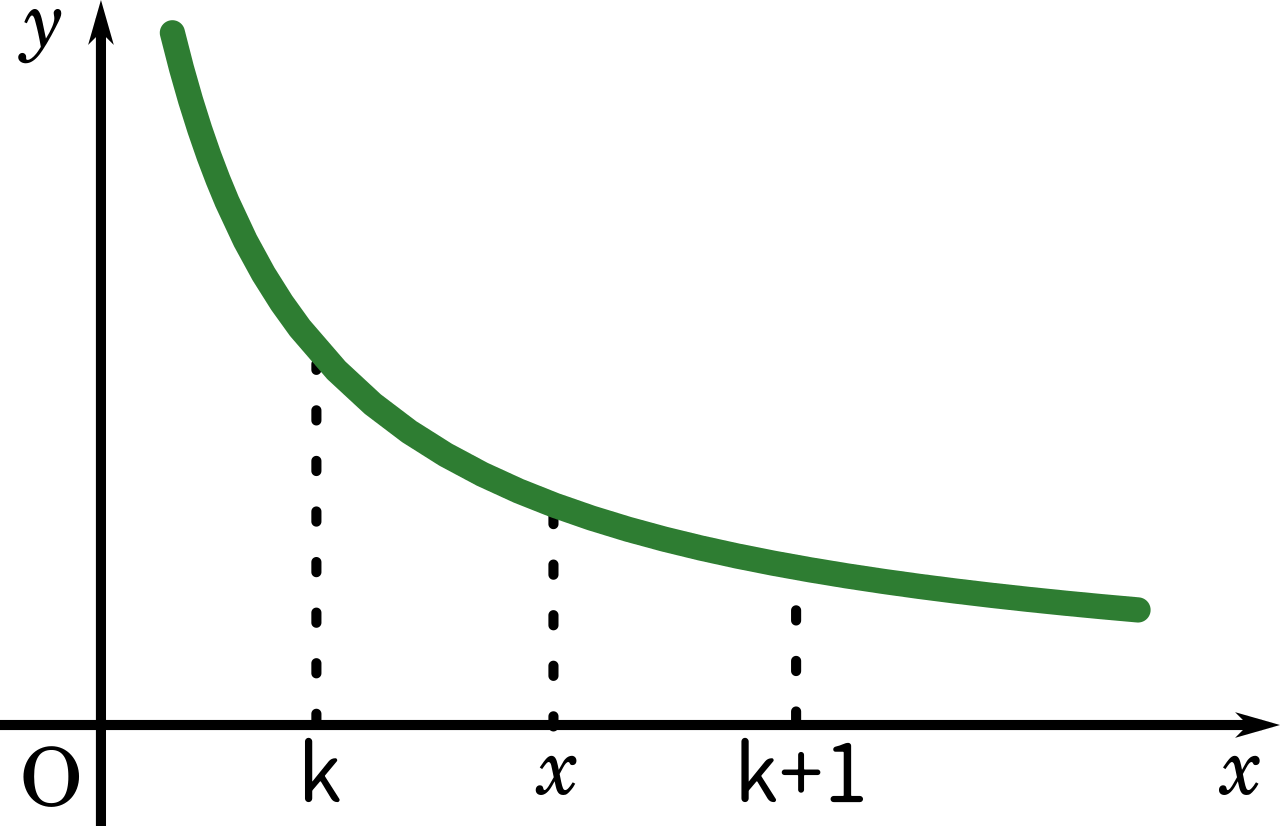
ここで、$\displaystyle\frac{1}{x}$ のグラフを考えると、

$\displaystyle\frac{1}{k+1}<\frac{1}{x}<\frac{1}{k}$ の関係が成り立ちます。

ここから各辺に $|\sin\pi x|$ をかけると
$\displaystyle\frac{|\sin\pi x|}{k+1}<\frac{|\sin\pi x|}{x}<\frac{|\sin\pi x|}{k}$
積分して
$\displaystyle\int_k^{k+1}\frac{|\sin\pi x|}{k+1}\enspace dx<\int_k^{k+1}\frac{|\sin\pi x|}{x}\enspace dx<\int_k^{k+1}\frac{|\sin\pi x|}{k}\enspace dx$
これは $x$ についての積分だから、$k$ は定数とみなします。よって、積分の外に追い出しても大丈夫です。
$\displaystyle\frac{1}{k+1}\int_k^{k+1}|\sin\pi x|\enspace dx<\int_k^{k+1}\frac{|\sin\pi x|}{x}\enspace dx<\frac{1}{k}\int_k^{k+1}|\sin\pi x|\enspace dx$
②より
$\displaystyle\frac{1}{k+1}\int_0^{1}\sin\pi y\enspace dy<\int_k^{k+1}\frac{|\sin\pi x|}{x}\enspace dx<\frac{1}{k}\int_0^{1}\sin\pi y\enspace dy$
この式はあくまで山1個分なので、これを $n$ 個並べると
$\displaystyle\sum_{k=1}^n\frac{1}{k+1}\int_0^{1}\sin\pi y\enspace dy<\sum_{k=1}^n\int_k^{k+1}\frac{|\sin\pi x|}{x}\enspace dx<\sum_{k=1}^n\frac{1}{k}\int_0^{1}\sin\pi y\enspace dy\\\displaystyle\sum_{k=1}^n\frac{1}{k+1}\int_0^{1}\sin\pi y\enspace dy<\int_1^{n+1}\frac{|\sin\pi x|}{x}\enspace dx<\sum_{k=1}^n\frac{1}{k}\int_0^{1}\sin\pi y\enspace dy$
さらに
$\displaystyle\frac{1}{\log n}\sum_{k=1}^n\frac{1}{k+1}\int_0^{1}\sin\pi y\enspace dy<\frac{1}{\log n}\int_1^{n+1}\frac{|\sin\pi x|}{x}\enspace dx<\frac{1}{\log n}\sum_{k=1}^n\frac{1}{k}\int_0^{1}\sin\pi y\enspace dy$

また、$\displaystyle \int_0^{1}\sin\pi y\enspace dy$ は計算すると $\displaystyle\frac{2}{\pi}$ になるので、定数です。よって、Σの外に追い出しましょう。

$\displaystyle\int_0^{1}\sin\pi y\enspace dy\cdot\displaystyle\frac{1}{\log n}\sum_{k=1}^n\frac{1}{k+1}<\frac{1}{\log n}\int_1^{n+1}\frac{|\sin\pi x|}{x}\enspace dx<\int_0^{1}\sin\pi y\enspace dy\cdot\frac{1}{\log n}\sum_{k=1}^n\frac{1}{k}$

まずは左側の式から極限を求めます。

$\displaystyle\sum_{k=1}^n\frac{1}{k+1}=\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}+\frac{1}{n+1}\\\displaystyle 1+\sum_{k=1}^n\frac{1}{k+1}=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}+\frac{1}{n+1}\\\displaystyle 1+\sum_{k=1}^n\frac{1}{k+1}-\frac{1}{n+1}=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}\\\displaystyle 1-\frac{1}{n+1}+\sum_{k=1}^n\frac{1}{k+1}=\sum_{k=1}^n\frac{1}{k}$

両辺に $\displaystyle\frac{1}{\log n}$ をかけると

$\displaystyle \frac{1}{\log n}-\frac{1}{(n+1)\log n}+\frac{1}{\log n}\sum_{k=1}^n\frac{1}{k+1}=\frac{1}{\log n}\sum_{k=1}^n\frac{1}{k}$

ここで $n\rightarrow\infty$ とすると

$\displaystyle 0-0+\lim_{n\rightarrow\infty}\frac{1}{\log n}\sum_{k=1}^n\frac{1}{k+1}=1\\\displaystyle\lim_{n\rightarrow\infty}\frac{1}{\log n}\sum_{k=1}^n\frac{1}{k+1}=1$

今度は右側を考えると

$\displaystyle\lim_{n\rightarrow\infty}\frac{1}{\log n}\sum_{k=1}^n\frac{1}{k}=1$

よって

$\displaystyle\int_0^{1}\sin\pi y\enspace dy<\lim_{n\rightarrow\infty}\frac{1}{\log n}\int_1^{n+1}\frac{|\sin\pi x|}{x}\enspace dx<\int_0^{1}\sin\pi y\enspace dy$

はさみうちの原理より

$\displaystyle\lim_{n\rightarrow\infty}\frac{1}{\log n}\int_1^{n+1}\frac{|\sin\pi x|}{x}\enspace dx=\int_0^{1}\sin\pi y\enspace dy=\frac{2}{\pi}$

（答え)