【数IA確率】正六角形の中にできる三角形と確率（基本レベル）(東京都立大2015理系第1問)

点 O を中心とする半径 1 の円に内接している正六角形 ABCDEF がある。A,B,C,D,E,F,O の 7 点から異なる 3 点を同時に選ぶとき，以下の問いに答えなさい。（東京都立大2015）

(1) 選んだ 3 点が一直線上に並ぶ確率を求めなさい。

(2) 選んだ 3 点を結ぶと正三角形ができる確率を求めなさい。

(3) 選んだ 3 点を結ぶと面積が $\cfrac{\sqrt{3}}{3}$ より大きい三角形ができる確率を求めなさい。

3 点が一直線上に並ぶ確率

(1)から始めます。

7 つの点から 3 点を選ぶので，全事象は

$_7C_3=\cfrac{7\cdot6\cdot5}{3\cdot2\cdot1}=35$

通りです。

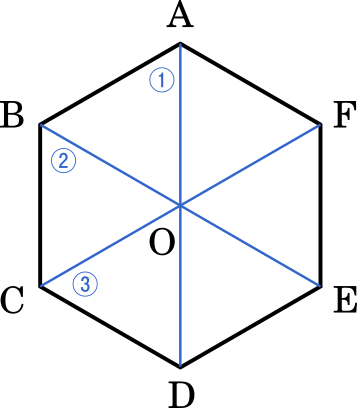
図を描いてみると，3 点が一直線上に並ぶ場合は 3 通りあることが分かります。

したがって $\cfrac{3}{35}$（答え）

正三角形ができる確率

(2)に進みます。

したがって

$\cfrac{8}{35}$　（答え）

三角形の面積を求める

(3)に進みます。

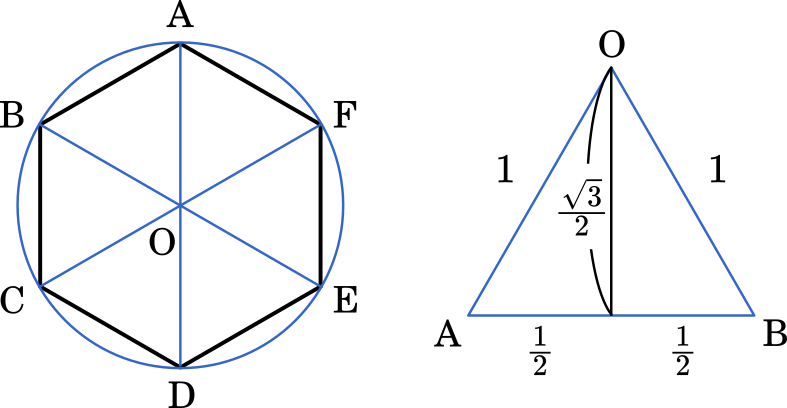
まず，(2)で作った小さい正三角形から考えてみましょう。

正三角形を 2 つに分けると，辺の比が $1:2:\sqrt{3}$ の三角形ができます。OA の長さが 1 であることから，他の辺の長さも求められます。

よって，△OABの面積は

$\cfrac{1}{2}\cdot1\cdot\cfrac{\sqrt{3}}{2}=\cfrac{\sqrt{3}}{4}$

となり，条件を満たしません。

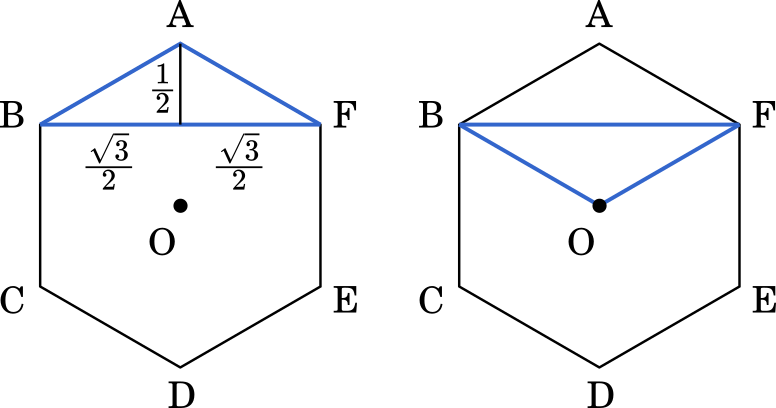
次に△ABFを考えてみます。これは同様に△OBFという形も作ることができ，同じ大きさです。

さきほど作った，$1:2:\sqrt{3}$ の関係から，辺の長さを求めて計算しましょう。

$\cfrac{1}{2}\cdot\sqrt{3}\cdot\cfrac{1}{2}=\cfrac{\sqrt{3}}{4}$

これも条件を満たしません。

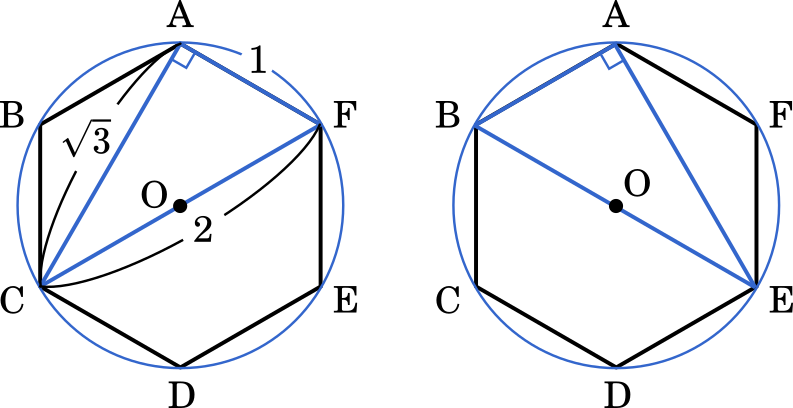
次に△ACFが作れます。このとき，∠CAF を考えると辺 CF が円の直径なので，∠CAF=90° であることが分かります。これも，辺の比が $1:2:\sqrt{3}$ の三角形です。面積は

$\cfrac{1}{2}\cdot1\cdot\sqrt{3}=\cfrac{\sqrt{3}}{2}$

これは条件を満たします。

そして，直角の部分が点 A にあるときから，点 F にあるときまで 6 個の三角形が作れます。

また，同様に △ABE という三角形も作れるので，これも同様に 6 個あります。

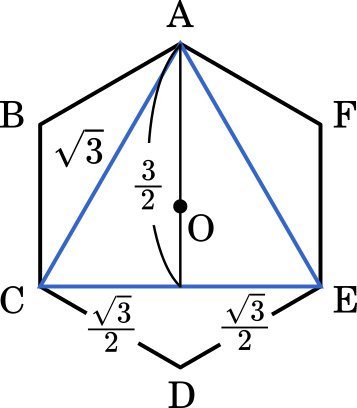
また，(2)で作った大きな正三角形がありました。面積は

$\cfrac{1}{2}\cdot\sqrt{3}\cdot\cfrac{3}{2}=\cfrac{3\sqrt{3}}{4}$

これは条件を満たします。

考えられる三角形のパターンは以上です。

したがって

$\cfrac{6+6+2}{35}=\cfrac{14}{35}$
$=\cfrac{2}{5}$　（答え）