三角形の面積比／四面体の面積比(横浜国立大2016理系第3問(文系第3問))

四面体 OABC があり，$\overrightarrow{\text{OA}}=\vec{a},\overrightarrow{\text{OB}}=\vec{b},\overrightarrow{\text{OC}}=\vec{c}$ とする。三角形 ABC の重心を G とする。点 D，E，P を $\overrightarrow{\text{OD}}=2\vec{b}$，$\overrightarrow{\text{OE}}=3\vec{c}$，$\overrightarrow{\text{OP}}=6\overrightarrow{\text{OG}}$ をみたす点とし，平面 ADE と直線 OP の交点を Q とする。次の問いに答えよ。

(1) $\overrightarrow{\text{OQ}}$ を $\vec{a},\vec{b},\vec{c}$ を用いて表せ。

(2) 三角形 ADE の面積を $S_1$，三角形 QDE の面積を $S_2$ とするとき，$\cfrac{S_2}{S_1}$ を求めよ。

(3) 四面体 OADE の体積を $V_1$，四面体 PQDE の体積を $V_2$ とするとき，$\cfrac{V_2}{V_1}$ を求めよ。

ベクトルを 2 通りで表す

(1)から始めます。

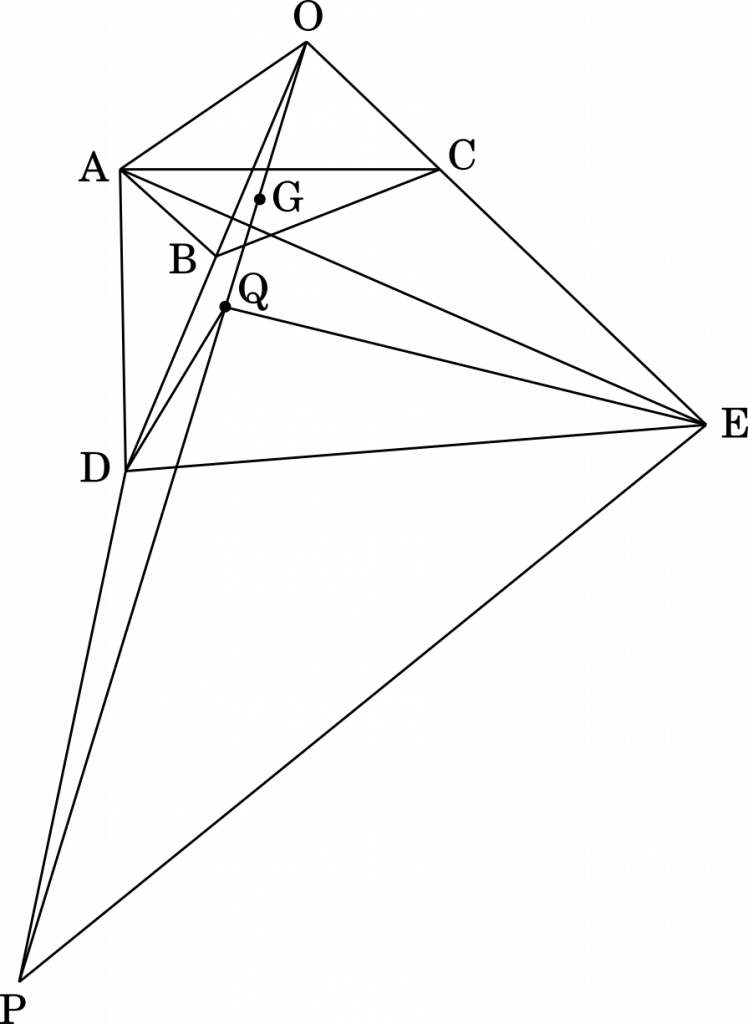
まず，点 Q は平面 ADE 上の点なので　
$\overrightarrow{\text{OQ}}=s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OD}}+u\overrightarrow{\text{OE}}$ $(s+t+u=1)$
$=s\vec{a}+2t\vec{b}+3u\vec{c}$

という式を立てます。

もちろん，この式だけでは何もできないので，次の手を考えます。

点 Q は OG の延長線上にあるので

$\overrightarrow{\text{OQ}}=k\overrightarrow{\text{OG}}$

と表すことができます。

そして，点 G は三角形 ABC の重心です。

三角形の重心を G とすると

$\overrightarrow{\text{OG}}=\cfrac{\overrightarrow{\text{OA}}+\overrightarrow{\text{OB}}+\overrightarrow{\text{OC}}}{3}$

$\overrightarrow{\text{OQ}}=\cfrac{k}{3}(\vec{a}+\vec{b}+\vec{c})$

ここで 2 つの式を比べると

$\overrightarrow{\text{OQ}}=s\vec{a}+2t\vec{b}+3u\vec{c}$
$\overrightarrow{\text{OQ}}=\cfrac{k}{3}\vec{a}+\cfrac{k}{3}\vec{b}+\cfrac{k}{3}\vec{c}$

$s=2t=3u=\cfrac{k}{3}$

という関係が成り立ちます。ここから

$s=2t$
$t=\cfrac{s}{2}$
$s=3u$
$u=\cfrac{s}{3}$

これを $s+t+u=1$ に代入すると

$s+\cfrac{s}{2}+\cfrac{s}{3}=1$

$6s+3s+2s=6$
$11s=6$
$s=\cfrac{6}{11}$

$s=\cfrac{k}{3}$ だから

$\overrightarrow{\text{OQ}}=\cfrac{6}{11}(\vec{a}+\vec{b}+\vec{c})$　（答え）

三角形の面積比

(2)に進みます。

AQ の延長線と DE の交点を R とします。R は DE 上の点だから

$\overrightarrow{\text{AR}}=s\overrightarrow{\text{AD}}+t\overrightarrow{\text{AE}}$　$(s+t=1)$

が成り立ちます。

$\overrightarrow{\text{AR}}=s(2\vec{b}-\vec{a})+t(3\vec{c}-\vec{a})$
$=-(s+t)\vec{a}+2s\vec{b}+3t\vec{c}$

また

$\overrightarrow{\text{AR}}=k\overrightarrow{\text{AQ}}$

$=k\Big\{\cfrac{6}{11}(\vec{a}+\vec{b}+\vec{c})-\vec{a}\Big\}$
$=-\cfrac{5}{11}k\vec{a}+\cfrac{6}{11}k\vec{b}+\cfrac{6}{11}k\vec{c}$

式を比べると

$\cfrac{5}{11}=s+t=1$
$k=\cfrac{11}{5}$

よって

$\overrightarrow{\text{AR}}=\cfrac{11}{5}\overrightarrow{\text{AQ}}$

が成り立つので，AQ：QR = 5 : 6

これは三角形の高さの比と等しくなります。底辺の等しい三角形の面積は高さに比例するので

したがって $\cfrac{S_2}{S_1}=\cfrac{6}{11}$　（答え）

体積の比を求める

(3)に進みます。

(2)より

△QDE = △ADE × $\cfrac{6}{11}$

高さが等しい四面体の体積は低面積に比例するので，四面体 OQDE の体積は四面体 OADE の $\cfrac{6}{11}$ です。

(3) 四面体 OADE の体積を $V_1$，四面体 PQDE の体積を $V_2$ とするとき，$\cfrac{V_2}{V_1}$ を求めよ。

四面体 OQDE と PQDE は底面積が等しく，体積の比は高さの比に等しくなります。そこで，高さの比を求めてみます。

$\overrightarrow{\text{OP}}=6\overrightarrow{\text{OG}}$ より

$\overrightarrow{\text{OP}}=6\cdot\cfrac{1}{3}(\vec{a}+\vec{b}+\vec{c})$
$=2(\vec{a}+\vec{b}+\vec{c})$

(1)より，$\overrightarrow{\text{OQ}}=\cfrac{6}{11}(\vec{a}+\vec{b}+\vec{c})$ だったので

OQ : OP = $\cfrac{6}{11}$ : 2 = 3 : 11

が成り立ち，これより

OQ : QP = 3 : 8

が成り立ちます。これが四面体の高さの比です。

$V_2=V_1\times\cfrac{6}{11}\times\cfrac{8}{3}$
$=\cfrac{16}{11}V_1$
$\cfrac{V_2}{V_1}=\cfrac{16}{11}$　（答え）