三角形が成り立つ条件と場合の数(神戸大2015文系第3問・理系第5問)

$a$，$b$，$c$ を 1 以上 7 以下の自然数とする。次の条件 (*) を考える。

(*) 3 辺の長さが $a$，$b$，$c$ である三角形と，3 辺の長さが $\cfrac{1}{a}$，$\cfrac{1}{b}$，$\cfrac{1}{c}$ である三角形が両方とも存在する。

以下の問に答えよ。

(1) $a=b>c$ であり，かつ条件 (*) をみたす $a$，$b$，$c$ の組の個数を求めよ。

(2) $a>b>c$ であり，かつ条件 (*) をみたす $a$，$b$，$c$ の組の個数を求めよ。

(3) 条件 (*) をみたす $a$，$b$，$c$ の組の個数を求めよ。

三角形が成り立つ条件

(1)から始めます。

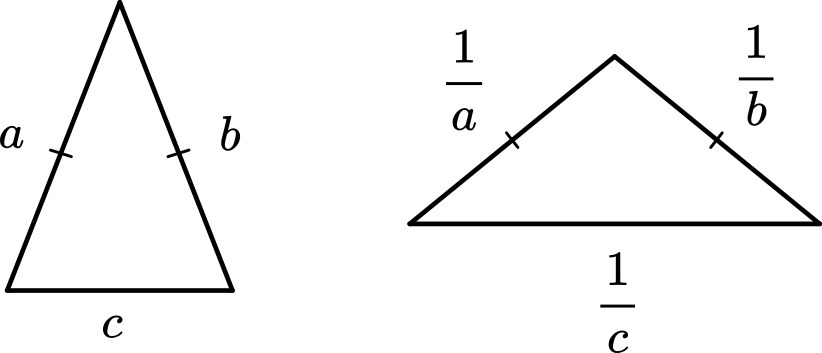
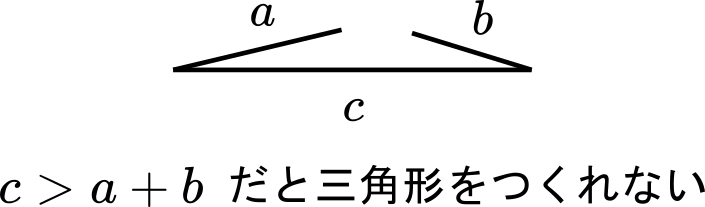
三角形の最も長い辺は残りの 2 つの辺の長さの和よりも小さくなければなりません。

$a=b>c$ ・・・①

まず，①は三角形が成り立つ条件をもともと満たしているので問題ありません。
次に，もう一つの三角形について考えると，三角形が成り立つ条件から

$\cfrac{1}{a}+\cfrac{1}{b}>\cfrac{1}{c}$

$a=b$ だから

$\cfrac{2}{a}>\cfrac{1}{c}$
$2c>a$　・・・②

①，②より

$c<a=b<2c$

あとは，これにあてはまる自然数を地道に探していきましょう。

・$c=1$ のとき

$1<a=b<2$

あてはまる，$a$，$b$ は存在しない。

・$c=2$ のとき

$2<a=b<4$

$a=b=3$ が当てはまります。よって，1 個。

・$c=3$ のとき

$3<a=b<6$

$a=b=4,5$ が当てはまります。よって，2 個。

・$c=4$ のとき

$4<a=b<8$

$a=b=5,6,7$ が当てはまります。よって，3 個。

・$c=5$ のとき

$5<a=b<10$

$a=b=6,7$ が当てはまります。$a$，$b$ は 7 以下の自然数であることを忘れずに。よって，2 個。

・$c=6$ のとき

$6<a=b<12$

$a=b=7$ のみ。よって 1 個。

・$c=7$ のとき

$7<a=b<14$

当てはまる $a$，$b$ は存在しない。

したがって

$1+2+3+2+1=9$　（答え）

さらに条件を考える

(2)に進みます。

まず，$a>b>c$ ・・・③ から，最も長い辺は $a$ だから，三角形が成り立つためには

$a<b+c$　・・・④

という条件が必要です。また

$\cfrac{1}{a}+\cfrac{1}{b}>\cfrac{1}{c}$

も，必要な条件です。変形すると

$\cfrac{c(a+b)}{ab}>1$　・・・⑤

もう少し不等式が整理できないものかと思いますが，肝心の答えが出せなければ意味がないので，このあたりであきらめて，③，④，⑤を満たす自然数の組を見つけていきましょう。

まず，$a>b>c$ から $a$ は 3 以上 7 以下ということになります。
$a=3$ とすると $(a,b,c)=(3,2,1)$ のみが③を満たしますが，$b+c=3$ となるので④を満たしません。

・$a=4$ のとき

$4>b>c$ と $4<b+c$ を満たす $b$ と $c$ を考えてみましょう。

まず，$4>b>c$ から $b$ は 2 か 3 です。

$b=2$ のとき $c=1$ ですが，$4<b+c$ を満たしません。$b=3$ のとき $c$ は 1 か 2 で，$4<b+c$ を満たすのは $c=2$ のときです。

さらに $(a,b,c)=(4,3,2)$ を⑤に代入すると
$\cfrac{2(4+3)}{4\cdot3}=\cfrac{14}{12}>1$

よって，$(a,b,c)=(4,3,2)$ はオッケーということになります。

・$a=5$ のとき

$5>b>c$ から $b$ は 2 以上 4 以下です。③，④を満たす組み合わせを探すと

$(b,c)=(4,2),(4,3)$

です。

あとはこれが⑤を満たすか確かめましょう

$\cfrac{2(5+4)}{5\cdot4}=\cfrac{18}{20}<1$　不適
$\cfrac{3(5+4)}{5\cdot4}=\cfrac{27}{20}>1$　適する

よって，$(a,b,c)=(5,4,3)$

・$a=6$ のとき

$6>b>c$ から $b$ は 2 以上 5 以下です。③，④を満たす組み合わせを考えます。

上で行った作業を振り返ると，小さい方から考えて $(b,c)=(4,3)$ になったときにはじめて $b$ と $c$ の和が 7 になるので，これより小さい値について考える必要はありません。

③，④を満たすのは

$(b,c)=(4,3),(5,2),(5,3),(5,4)$

⑤を満たすか確かめます

$\cfrac{3(6+4)}{6\cdot4}=\cfrac{30}{24}>1$　適する
$\cfrac{2(6+5)}{6\cdot5}=\cfrac{22}{30}<1$　不適
$\cfrac{3(6+5)}{6\cdot5}=\cfrac{33}{30}>1$　適する
$\cfrac{4(6+5)}{6\cdot5}=\cfrac{44}{30}>1$　適する

⑤を満たすのは

$(a,b,c)=(6,4,3),(6,5,3),(6,5,4)$

・$a=7$ のとき

$7>b>c$ から，$b$ は 2 以上 6 以下。③，④を満たすのは

$(b,c)=(5,3),(5,4),(6,2),(6,3),(6,4),(6,5)$

⑤を満たすかどうか確かめると

$\cfrac{3(7+5)}{7\cdot5}=\cfrac{36}{35}>1$　適する
$\cfrac{4(7+5)}{7\cdot5}=\cfrac{48}{35}>1$　適する
$\cfrac{2(7+6)}{7\cdot6}=\cfrac{26}{42}<1$　不適
$\cfrac{3(7+6)}{7\cdot6}=\cfrac{39}{42}<1$　不適
$\cfrac{4(7+6)}{7\cdot6}=\cfrac{52}{42}>1$　適する
$\cfrac{5(7+6)}{7\cdot6}=\cfrac{65}{42}>1$　適する

⑤を満たすのは
$(a,b,c)=(7,5,3),(7,5,4),(7,6,4),(7,6,5)$

したがって，条件を満たす $a,b,c$ の組の個数は 9 個。（答え）

不等式のパターンを考える

(3)に進みます。

(1)，(2)の答えを利用して，$a,b,c$ の間に成り立つ等式・不等式のパターンを考えてみます。

まず，(1)のようなパターンは

$a=b>c$，$b=c>a$，$c=a>b$ の 3 通りがあります。そして，組み合わせはそれぞれ 9 個ずつあるので，全体で $3\times9=27$ 個です。

次に，$a>b=c$ のようなパターンも考えられます。これも上と同じように 27 個あります。

また，$a>b>c$ のパターンもありました。文字の順番を並べかえると $3!$ 通りがあります。よって，全体で $3!\times9=54$ 個です。

最後に，$a=b=c$，つまり正三角形のパターンも忘れないようにしましょう。これは，$(a,b,c)=(1,1,1)$ から $(7,7,7)$ まで 7 個です。

したがって

$27+27+54+7=115$　（答え）