三角関数と二次関数の融合問題(東京都立大2016文系第4問)

$\theta$ は $0\leqq\theta<2\pi$ をみたす実数とする。

$f(x)=x^2-(2\cos\theta)x-\sin^2\theta+\sin\theta+\cfrac{1}{2}$
とおくとき，以下の問いに答えなさい。（東京都立大2016）

(1) 放物線 $y=f(x)$ の頂点を求めなさい。

(2) 方程式 $f(x)=0$ が異なる 2 つの実数解をもつような $\theta$ の範囲を求めなさい。

(3) $\theta$ が(2)で求めた範囲を動くとき，放物線 $y=f(x)$ と $x$ 軸で囲まれる図形の面積を $S(\theta)$ とする。$S(\theta)$ を最大にする $\theta$ の値と，$S(\theta)$ の最大値を求めなさい。

平方完成

(1)から始めます。

頂点を求めるので，式を平方完成しましょう。

$f(x)=(x-\cos\theta)^2-\cos^2\theta-\sin^2\theta+\sin\theta+\cfrac{1}{2}$
$=(x-\cos\theta)^2-1+\sin\theta+\cfrac{1}{2}$
$=(x-\cos\theta)^2+\sin\theta-\cfrac{1}{2}$

頂点の座標は $\Big(\cos\theta,\space\sin\theta-\cfrac{1}{2}\Big)$　（答え）

判別式を求める

(2)に進みます。

判別式を作り，$D>0$ であれば異なる 2 つの実数解が存在することになります。

$\cfrac{D}{4}=\cos^2\theta+\sin^2\theta-\sin\theta-\cfrac{1}{2}$
$=1-\sin\theta-\cfrac{1}{2}$
$=\cfrac{1}{2}-\sin\theta>0$
$\sin\theta<\cfrac{1}{2}$

$0\leqq\theta<2\pi$ より

$0\leqq\theta<\cfrac{\pi}{6}$，$\cfrac{5\pi}{6}<\theta<2\pi$　（答え）

6分の1公式で面積を求める

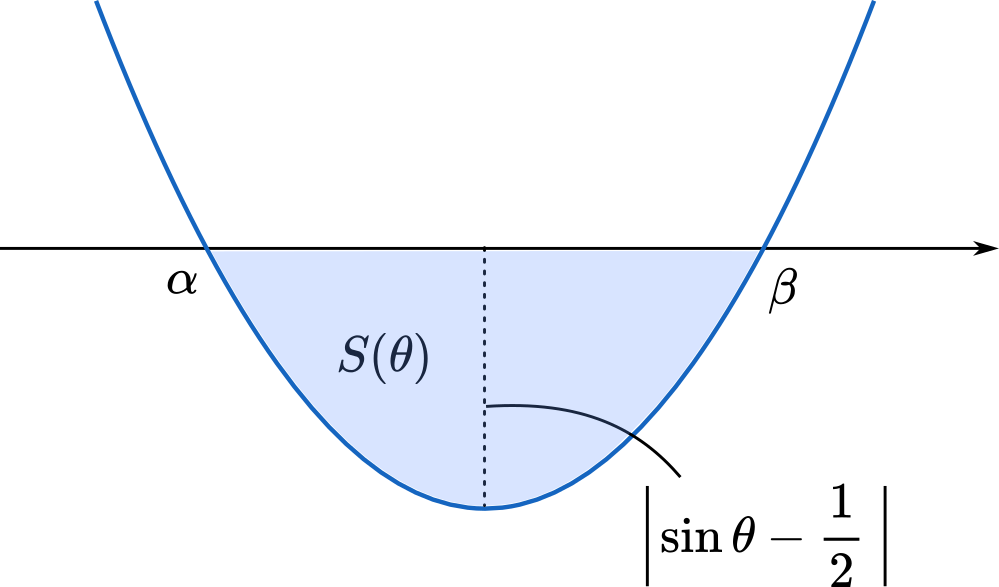
$f(x)=0$ の解を $\alpha,\beta$ とすると，6分の1公式を使って面積を求めることができます。

$\theta=\cfrac{3\pi}{2}$ のとき，$\Big|\sin\theta-\cfrac{1}{2}\Big|$ は最大となるので，$S(\theta)$ も最大となる。

これを当てはめて面積を求めましょう。まず，$\beta-\alpha$ を考えます。

$\alpha=\cos\theta-\sqrt{\frac{D}{4}}$
$\beta=\cos\theta+\sqrt{\frac{D}{4}}$

よって

$\beta-\alpha=2\sqrt{\frac{D}{4}}$

(2)で $\cfrac{D}{4}$ を求めています。

$=2\sqrt{\cfrac{1}{2}-\sin\theta}$

$\theta=\cfrac{3\pi}{2}$ より

$=2\sqrt{\cfrac{1}{2}+1}$
$=2\sqrt{\cfrac{3}{2}}$
$=2\cdot\cfrac{\sqrt{6}}{2}$
$=\sqrt{6}$

したがって

$S(\theta)=\cfrac{(\sqrt{6})^3}{6}$
$=\sqrt{6}$　（答え）