三角関数の微分と積分(横浜国立大2020理系第1問)

(1) 関数 $f(x)=(e^x-1)\cos x-\sin x$　$\Big(-\cfrac{\pi}{2}\leqq x\leqq\cfrac{\pi}{2}\Big)$ の増減，極値を調べ，そのグラフの概形を描け。ただし，グラフの凹凸，変曲点は調べなくてよい。

(2)　定積分

$\displaystyle\int_{\small{\frac{\pi}{6}}}^{\small{\frac{\pi}{4}}}\cfrac{\log(\sin x)}{\tan x}\space dx$
を求めよ。

三角関数の微分

(1)から始めます。

ここはいくつかの公式を使いながら，微分していきましょう。

$f(x)=(e^x-1)\cos x-\sin x$

$f'(x)=(e^x-1)’\cos x+(e^x-1)(\cos x)’-\cos x$
$=e^x\cos x-(e^x-1)\sin x-\cos x$
$=-(e^x-1)\sin x+(e^x-1)\cos x$
$=(1-e^x)(\sin x-\cos x)$

三角関数の合成より

$=(1-e^x)\cdot\sqrt{2}\sin\Big(x-\cfrac{\pi}{4}\Big)$
$=\sqrt{2}(1-e^x)\sin\Big(x-\cfrac{\pi}{4}\Big)$

増減表を作るために，微分して極値を求めます。

$\sqrt{2}(1-e^x)\sin\Big(x-\cfrac{\pi}{4}\Big)=0$　として

式が 0 になるのは，$1-e^x$ が 0 になるときと $\sin$ の値が 0 になるときです。

$1-e^x=0$
$e^x=1$
$x=0$

また

$\sin\Big(x-\cfrac{\pi}{4}\Big)=0$
$x-\cfrac{\pi}{4}=0$
$x=\cfrac{\pi}{4}$

増減表は

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|c|c|}\hline x&-\frac{\pi}{2}&\cdots&0&\cdots&\frac{\pi}{4}&\cdots&\frac{\pi}{2}\\\hline f'(x)&-&-&0&+&0&-&-\\\hline f(x)&1&\searrow&0&\nearrow&\frac{e^{\frac{\pi}{4}}-2}{\sqrt{2}}&\searrow&-1\\\hline\end{array}$

$f\Big(-\cfrac{\pi}{2}\Big)=(e^{\small{\frac{\pi}{2}}}-1)\cos\Big(-\cfrac{\pi}{2}\Big)-\sin\Big(-\cfrac{\pi}{2}\Big)$
$=(e^{\small{\frac{\pi}{2}}}-1)\cdot0-(-1)$
$=1$

$f\Big(\cfrac{\pi}{2}\Big)=(e^{\small{\frac{\pi}{2}}}-1)\cos\cfrac{\pi}{2}-\sin\cfrac{\pi}{2}$
$=(e^{\small{\frac{\pi}{2}}}-1)\cdot0-1$
$=-1$

$f(0)=(e^0-1)\cos0-\sin0$
$=(1-1)\cdot1-0$
$=0$

$f\Big(\cfrac{\pi}{4}\Big)=(e^{\small{\frac{\pi}{4}}}-1)\cfrac{1}{\sqrt{2}}-\cfrac{1}{\sqrt{2}}$
$=\cfrac{e^{\small{\frac{\pi}{4}}}-2}{\sqrt{2}}$

グラフは

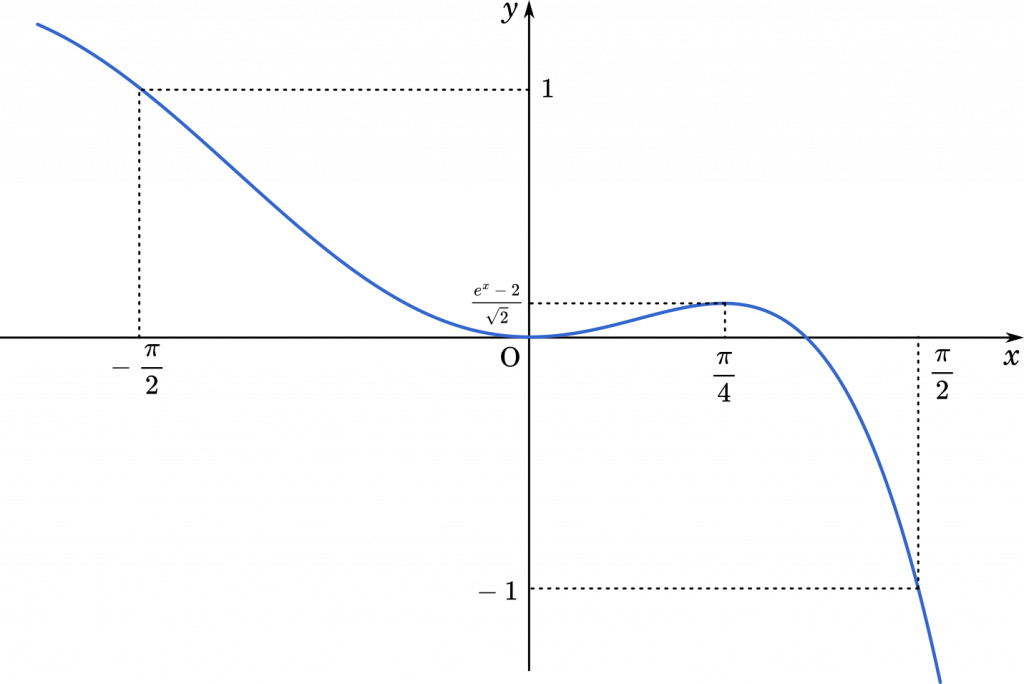
したがって

$x=0$ のとき，最小値 $0$
$x=\cfrac{\pi}{4}$ のとき，最大値 $\cfrac{e^{\small{\frac{\pi}{4}}}-2}{\sqrt{2}}$

（答え）

I を用いた積分

(2)に進みます。

この積分は置換積分です。

いったん，不定積分の形で解いていきます。

$\displaystyle\int\frac{\log(\sin x)}{\tan x}\space dx$
$\displaystyle=\int\frac{\log(\sin x)}{\cfrac{\sin x}{\cos x}}\space dx$
$\displaystyle=\int\frac{\log(\sin x)}{\sin x}\cdot\cos x\space dx$

$\sin x=t$ とおくと

$\cos x\space dx=dt$

式全体を $I$ とします。

$\displaystyle I=\int\cfrac{\log t}{t}\space dt$
$\displaystyle=\int(\log t)’\log t\space dt$

部分積分を用いましょう。

$\displaystyle=(\log t)^2+C-\int\cfrac{\log t}{t}\space dt$
$I=(\log t)^2+C-I$
$2I=(\log t)^2+C$
$I=\cfrac{1}{2}(\log t)^2+C$ ($C$は積分定数)

$\def\arraystretch{1.5}\begin{array}{|c|ccc|}\hline x&\frac{\pi}{6}&\rightarrow&\frac{\pi}{4}\\\hline t&\frac{1}{2}&\rightarrow&\frac{\sqrt{2}}{2}\\\hline\end{array}$

$\displaystyle F(x)=\int_{\small{\frac{\pi}{6}}}^{\small{\frac{\pi}{4}}}\cfrac{\log(\sin x)}{\tan x}\space dx$　とすると

$=\cfrac{1}{2}\Big[(\log t)\Big]_{\small{\frac{1}{2}}}^{\small{\frac{\sqrt{2}}{2}}}$
$=\cfrac{1}{2}\Big\{\Big(\log\cfrac{\sqrt{2}}{2}\Big)^2-\Big(\log\cfrac{1}{2}\Big)^2\Big\}$
$=\cfrac{1}{2}\Big\{\Big(\log\cfrac{\sqrt{2}}{2}+\log\cfrac{1}{2}\Big)\Big(\log\cfrac{\sqrt{2}}{2}-\log\cfrac{1}{2}\Big)\Big\}$

ここで

$\log\cfrac{\sqrt{2}}{2}+\log\cfrac{1}{2}=\log\cfrac{\sqrt{2}}{2}\cdot\cfrac{1}{2}$
$=\log\cfrac{\sqrt{2}}{4}$

指数に直して整理します。

$=\log\cfrac{2^{\small{\frac{1}{2}}}}{2^2}$
$=\log2^{\small{\frac{1}{2}-2}}$
$=\log2^{\small{-\frac{3}{2}}}$
$=-\cfrac{3}{2}\log 2$

また

$\log\cfrac{\sqrt{2}}{2}-\log\cfrac{1}{2}$
$=\log\cfrac{\cfrac{\sqrt{2}}{2}}{\cfrac{1}{2}}$
$=\log\sqrt{2}$
$=\log2^{\small{\frac{1}{2}}}$
$=\cfrac{1}{2}\log 2$

よって

$F(x)=\cfrac{1}{2}\Big(-\cfrac{3}{2}\log2\Big)\Big(\cfrac{1}{2}\log 2\Big)$
$=-\cfrac{3}{8}(\log2)^2$　（答え）