【数Ⅲ】サイクロイドの速度と道のり

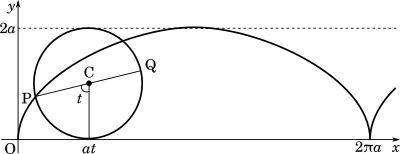
半径 $a$ の円が $x$ 軸上を滑ることなく正の方向に回転していくとき，円周上の2つの定点 P と Q の運動について考える。時刻 $t = 0$ のとき P は原点 O にあり，Q は点 $(0, 2a)$ にある。円は毎秒 1 ラジアンの速さで回転する。このとき，点 P の時刻 $t$ における座標 $(x, y)$ は
$x = a(t − \sin t)$，$y = a(1 − \cos t)$
で表される。以下の問いに答えよ。(長崎大2018)

座標を求める

(1) 時刻 $t$ における円の中心 C と点 Q の座標を，それぞれ求めよ。

---

Cの座標は円の半径が$a$であることから、図を見れば簡単に求められます。

C$(at,a)$　（答え）

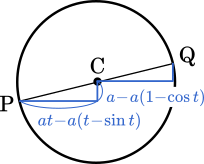
PCの変位はCの座標からPの座標を引けば求められます。
$(at-a(t-\sin t)),\space a-a(1-\cos t))$
$=(a\sin t,\space a\cos t)$

Cの座標にこれを足せばQになります。
$(at+a\sin t,\space a+a\cos t)$
=$(a(t+\sin t),\space a(1+\cos t))$　（答え）

速さを求める

(2) 時刻 $t$ における点 P の速度ベクトル $\displaystyle \overrightarrow{v_P} = \left(\frac{dx}{dt},\frac{dy}{dt}\right)$ を求めよ。また，時刻 $t$ が $0 \leqq t \leqq 2\pi$ の範囲において，速さ $|\overrightarrow{v_P}|$ の最大値と最小値，およびその時の P の座標を求めよ。

---

$x=a(t-\sin t)$ より
$\displaystyle \frac{dx}{dt}=a(1-\cos t)$
$y=a(1-\cos t)$ より
$\displaystyle \frac{dy}{dt}=a\sin t$
よって、$\overrightarrow{v_P}=(a(1-cos t),a\sin t))$

$|\overrightarrow{v_P}|^2=a^2(1-\cos t)^2+a^2\sin^2 t$
$=a^2(1-2\cos t+\cos^2 t)+a^2\sin^2 t$
$=a^2-2a^2\cos t+a^2\cos^2 t+a^2\sin^2 t$
$=a^2-2a^2\cos t+a^2(\sin^2 t+\cos^2 t)$
三角比の公式 $\sin^2 x+\cos^2 x=1$ より
$=a^2-2a^2\cos t+a^2$
$=2a^2(1-\cos t)$

$|\overrightarrow{v_P}|^2=2a^2(1-\cos t)$
$\cos t=-1$ のとき最大
$|\overrightarrow{v_P}|^2=2a^2(1+1)=4a^2$
$|\overrightarrow{v_P}|=2a$
また
$\cos t=-1$
$t=\pi$
したがって、最大値は $t=\pi$ のとき $2a$　（答え）
$t=\pi$ を点Pに代入すると
P$(a(\pi-\sin\pi),a(1-\cos\pi))$
=P$(a\pi,2a)$　（答え）

また、最小値を求めると
$\cos t=1$ のとき最小
$|\overrightarrow{v_P}|^2=2a^2(1-1)=0$
$|\overrightarrow{v_P}|=0$
また
$\cos t=1$
$t=0,2\pi$
したがって、最小値は $t=0,2\pi$ のとき $0$　（答え）

$t=0$ を点Pに代入すると
P$(a(0-\sin 0),a(1-\cos 0))$
P$(0,0)$ （答え）
$t=2\pi$ を点Pに代入すると
P$(a(2\pi-\sin 2\pi),a(1-\cos 2\pi))$
=P$(2\pi a,0)$ （答え）

速度ベクトルを求める

(3) 時刻 $t$ における点 Q の速度ベクトル $\overrightarrow{v_Q}$ を求めよ。さらに，内積 $\overrightarrow{v_P}\cdot\overrightarrow{v_Q}$ を求めよ。

---

$\displaystyle \overrightarrow{v_Q}=\left(\frac{dx}{dt},\frac{dy}{dt}\right)$

$\displaystyle\frac{dx}{dt}=a(1+\cos t)$
$\displaystyle\frac{dy}{dt}=-a\sin t$
したがって
$\overrightarrow{v_Q}=(a(1+\cos t),-a\sin t)$ （答え）

$\overrightarrow{v_P}\cdot\overrightarrow{v_Q}=a(1-\cos t)\cdot a(1+\cos t)+a\sin t(-a\sin t)$
$=a^2(1-\cos^2 t)-a^2\sin^2 t$
$=a^2-a^2\cos^2 t-a^2\sin^2 t$
$=a^2-a^2(\sin^2 t+\cos^2 t)$
三角比の公式 $\sin^2 x+\cos^2 x=1$ より
$=a^2-a^2=0$　（答え）

道のりを求める

(4) 時刻 $t = \cfrac{\pi}{2}$ から $t=\cfrac{3\pi}{2}$ までの間に点 P が動く道のり $L_P$ と，点 Q が動く道のり $L_Q$ を，それぞれ求めよ。

---

$\displaystyle L_P=\int_{\small{\cfrac{\pi}{2}}}^{\small{\cfrac{3}{2}}\pi}|\overrightarrow{v_P}|dt=\int_{\small{\cfrac{\pi}{2}}}^{\small{\cfrac{3}{2}\pi}}|\sqrt{2a^2(1-\cos t)}|dt$

$\sin^2 x=\cfrac{1-\cos 2x}{2}$

$2\sin^2 x=1-\cos 2x$ より

$\displaystyle =\int_{\small{\cfrac{\pi}{2}}}^{\small{\cfrac{3}{2}\pi}}\left|\sqrt{2a^2\cdot 2\sin^2 \cfrac{t}{2}}\right|dt$

$\displaystyle =\int_{\small{\cfrac{\pi}{2}}}^{\small{\cfrac{3}{2}\pi}}2a\left|\sin\cfrac{t}{2}\right|dt$

$=-2a\left|\left[\cos\cfrac{t}{2}\cdot 2\right]_{\small{\cfrac{\pi}{2}}}^{\small{\cfrac{3}{2}\pi}}\right|$

$=-4a\left|\left[\cos\cfrac{t}{2}\right]_{\cfrac{\pi}{2}}^{\cfrac{3}{2}\pi}\right|$

$=-4a\left(\cos\cfrac{3}{4}\pi-\cos\cfrac{\pi}{4}\right)$

$\displaystyle =-4a\left(-\cfrac{\sqrt{2}}{2}-\cfrac{\sqrt{2}}{2}\right)$

$=4\sqrt{2}a$　（答え）

$\displaystyle L_Q=\int_{\small{\cfrac{\pi}{2}}}^{\small{\cfrac{3}{2}\pi}}|\overrightarrow{v_Q}|dt=\int_{\small{\cfrac{\pi}{2}}}^{\small{\cfrac{3}{2}\pi}}|\sqrt{2a^2(1+\cos t)}|dt$

$\displaystyle \cos^2 x=\cfrac{1+\cos 2x}{2}$

$2\cos^2 x=1+\cos 2x$ より

$\displaystyle =\int_{\small{\cfrac{\pi}{2}}}^{\small{\cfrac{3}{2}\pi}}\left|\sqrt{2a^2\cdot 2\cos^2 \cfrac{t}{2}}\right|dt$

$\displaystyle =\int_{\small{\cfrac{\pi}{2}}}^{\small{\cfrac{3}{2}\pi}}2a\left|\cdot 2\cos^2 \cfrac{t}{2}\right|dt$

$t$ が $\cfrac{\pi}{2}\rightarrow\cfrac{3}{2}\pi$ と変化するとき

$\cfrac{t}{2}$ は $\cfrac{\pi}{4}\rightarrow\cfrac{\pi}{2}\rightarrow\cfrac{3}{4}\pi$ と変化するので

$\cfrac{\pi}{2}\rightarrow\cfrac{3}{4}\pi$ のとき $\cos$ はマイナスになる

$\cfrac{t}{2}=\cfrac{\pi}{2} \hArr t=\pi$ だから

$\displaystyle =\int_{\small{\cfrac{\pi}{2}}}^{\pi} 2a\cos \cfrac{t}{2}dt-\int_{\pi}^{\small{\cfrac{3}{2}}\pi}2a\cos\cfrac{t}{2}dt$

$=2a\left[\sin\cfrac{t}{2}\cdot 2\right]_{\small{\cfrac{\pi}{2}}}^\pi – 2a\left[\sin\cfrac{t}{2}\cdot 2\right]_\pi^{\small{\cfrac{3}{2}\pi}}$

$=4a\left(\sin\cfrac{\pi}{2}-\sin\cfrac{\pi}{4}\right)-4a\left(\sin\cfrac{3}{4}\pi-\sin\cfrac{\pi}{2}\right)$

$=4a\left(1-\cfrac{\sqrt{2}}{2}\right)-4a\left(\cfrac{\sqrt{2}}{2}-1\right)$

$=8a-4\sqrt{2}a$

$=4(2-\sqrt{2})a$ （答え）