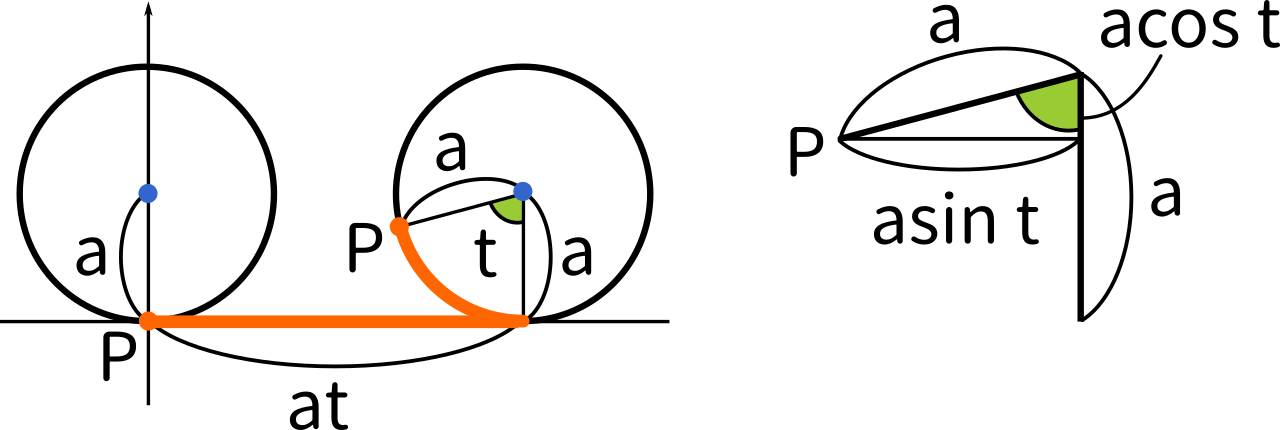中心 $(0,a)$, 半径 $a$ の円を $xy$ 平面上の $x$ 軸の上を $x$ の正の方向に滑らないように転がす。このとき円上の定点 $P$が原点 $(0,0)$を出発するとする。次の問いに答えよ。(九州大2010)
(1) 円が角 $t$ だけ回転したとき、点 $P$ の座標を求めよ。
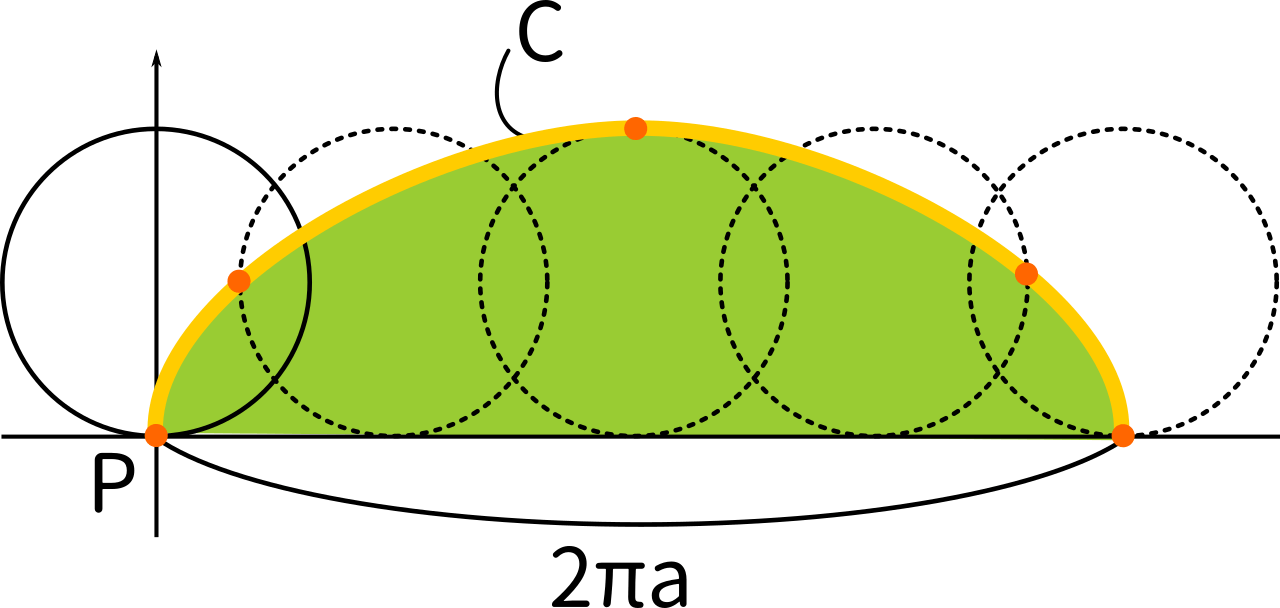
(2) $t$ が $0$ から $2t$ まで動いて円が一回転したときの点 $P$ の描く曲線を $C$ とする。曲線 $C$ と$x$ 軸とで囲まれる部分の面積を求めよ。
(3) 曲線 $C$ の長さを求めよ。
イメージとしてはこんな感じ。この軌跡をサイクロイドと言う。
大量生産された下っ端のロボット兵っぽい名前ですね。
弧の長さ=移動距離の関係で解決
問題文の条件を図にすると上のようになります。円が転がっていくことから、オレンジの2つの線は同じ長さになります(見えやすくするため2つの円を離して書いているので図の上では同じ長さに見えません)。
このとき、このオレンジの線の長さは $at$ となります。数Ⅱの三角関数で弧度法を習ったときにこの公式も習いました。
半径 $r$、中心角 $\theta$ (ラジアン)の扇形の弧の長さ $l$ は
$l=r\theta$
大学入試問題では、角度は基本的に弧度法で考えるものだと思って。半径に角度をかければ弧の長さになる。
また、上の図のように三角形を作ると、縦の長さは $a\cos t$、横の長さは $a\sin t$ であることが分かります。
三角比の基本に戻りましょう。$\displaystyle\sin t=\frac{\text{高さ}}{\text{斜辺}}$ でした。それに斜辺をかけると、$\displaystyle\text{斜辺}\times\sin t=\text{斜辺}\cdot\frac{\text{高さ}}{\text{斜辺}}=\text{高さ}$ となり、高さを求めることができます。同様に $\displaystyle\text{斜辺}\times\cos t=\text{斜辺}\cdot\frac{\text{底辺}}{\text{斜辺}}=\text{底辺}$ となるのです。
ここから、点 $P$ の $x$ 座標は
$x=at-a\sin t=a(t-\sin t)$
また、$y$ 座標は
$y=a-a\cos t=a(1-\cos t)$
よって、点 $P$ の座標は
$(a(t-\sin t),a(1-\cos t))$ (答え)
サイクロイドで囲まれた図形の面積を求める
次にサイクロイドで囲まれた部分の面積を求めてみましょう。面積を求めるときは積分でした。
んー、$\int a(1-\cos t)\enspace dt$ ですか?
気持ちは分かるけど、それをやらないようにね。横軸は $x$ だから、$dt$ じゃなくて $dx$ の積分にしないとダメよ。
横軸を $x$ とすると面積を求める式は
$\displaystyle\int_0^{2\pi a} y\enspace dx$
となります。ここから文字を置換して $t$ の積分にします。
ここで、
$y=a(1-\cos t)\\x=a(t-\sin t)$
より
$dx=a(1-\cos t)dt$
$x\enspace0\rightarrow2\pi a\\t\enspace 0\rightarrow 2\pi$
よって
$\displaystyle\int_0^{2\pi}a(1-\cos t)\cdot a(1-\cos t)\enspace dt\\\displaystyle=a^2\int_0^{2\pi}(1-\cos t)^2\enspace dt\\\displaystyle=a^2\int_0^{2\pi} 1-2\cos t+\cos^2 t\enspace dt\\$
積分でサインやコサインの2乗という形が出てきたときは、半角の公式を使って対処するのがセオリ―です。
$\displaystyle=a^2\int_0^{2\pi}1-2\cos t+\frac{1+\cos 2t}{2}\enspace dt\\\displaystyle=\frac{a^2}{2}\int_0^{2\pi} 2-4\cos t+1+\cos 2t\enspace dt\\\displaystyle=\frac{a^2}{2}\int_0^{2\pi}3-4\cos t+\cos 2t\enspace dt\displaystyle=\frac{a^2}{2}\left[3t-4\sin t+\sin 2t\cdot\frac{1}{2}\right]_0^{2\pi}\\\displaystyle=\frac{a^2}{2}\cdot6\pi=3\pi a^2$(答え)
$\int a(1-\cos t)dx$ ってしたら $x$ 以外の文字は定数だから、$=[ax-a\cos t\cdot x]$ みたいにしたらダメなんですか?
だめよ。$t$ は定数ではないから。$x=a(t-\sin t)$ ってなってるでしょ?これは $x$ の値によって $t$ の値も変化するっていうこと。つまり $\cos t$ は $t$ の中に $x$ で表す式が入っていて、合成関数になってるの。だから定数項として考えたらダメ。
曲線の長さを求める
媒介変数表示された曲線の長さ
曲線 $x=f(x),y=g(t) (a\text{≦}t\text{≦}b) $ の長さ $L$ は
$\displaystyle L=\int_a^b \sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}\enspace dt$
ざっくり言うと三平方の定理だよね。三角形の底辺と高さをそれぞれ微分して、めちゃくちゃ小さい三角形を作るの。そこから三平方の定理で斜めの長さを求めて、積分で積み上げるってのがイメージ。
$x=a(t-\sin t)\\\displaystyle\frac{dx}{dt}=a(1-\cos t)\\\displaystyle\left(\frac{dx}{dt}\right)^2=a^2(1-2\cos t+\cos^2 t)$
また
$y=a(1-\cos t)\\\displaystyle\frac{dy}{dt}=a\sin t\\\displaystyle\left(\frac{dy}{dt}\right)^2=a^2\sin^2 t$
よって
$\displaystyle\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2=a^2(1-2\cos t+\cos^2 t+\sin^2 t)\\=a^2(1-2\cos t+1)\\=a^2(2-2\cos t)\\=2a^2(1-\cos t)$
失敗したら別の戦略を考える―トライ&エラーで積分を突破する
$\displaystyle\int_0^{2\pi} \sqrt{2a^2(1-\cos t)}\enspace dt\\\displaystyle=\sqrt{2}a\int_0^{2\pi}\sqrt{1-\cos t}\enspace dt\\\displaystyle=\sqrt{2}a\int_0^{2\pi}(1-\cos t)^\frac{1}{2}\enspace dt\\\displaystyle=\sqrt{2}a\left[\frac{2}{3}(1-\cos t)^\frac{3}{2}\cdot\frac{1}{\sin t}\right]_0^{2\pi}$
$\sin t$ に $2\pi$ 代入したら $0$ になりますよ。
そうね。$0$ の除算はアウトだったね。つまり、積分失敗。
えー!失敗なんですか。じゃあ、どうしたらいいんですか?
大学入試レベルの積分って失敗するのが普通。人間は失敗から学ぶ生き物なのよ。
半角の公式を加工してみる
どう考えても $\sqrt{1-\cos t}$ の積分がうまく処理できません。ルートがついているのがやっかいです。では、このルートを外す方法はないかと考えます。
ルートの中が何かの2乗であれば、$\sqrt{3^2}=3$ みたいな感じでルート外れるよね。
今まで習った公式で、$1-\cos t$ みたいな形のヤツない?部分的でいいんだけど。
この方針で、$1-\cos t$ を加工します。このとき、この形が半角の公式に似ていることに気づけば、問題解決です。
$\displaystyle\sin^2 t=\frac{1-\cos 2t}{2}\\\displaystyle\sin^2\frac{t}{2}=\frac{1-\cos t}{2}\\\displaystyle 2\sin^2\frac{t}{2}=1-\cos t$
よって
$\displaystyle L=\int_0^{2\pi} \sqrt{2a^2\cdot2\sin^2\frac{t}{2}}\enspace dt\\\displaystyle=2a\int_0^{2\pi} \sin\frac{t}{2}\enspace dt\\\displaystyle=2a\left[-\cos\frac{t}{2}\cdot2\right]_0^{2\pi}\\\displaystyle=-4a\left[\cos\frac{t}{2}\right]_0^{2\pi}\\=-4a(\cos\pi-\cos0)\\=-4a(-1-1)\\=8a$
(答え)
自分の頭で考えると言っても、問われるのはあくまでこれまで学んできた知識をどう組み合わせるかです。教科書で学んだ知識を表面上だけでなくどれだけちゃんと理解して使いこなすことができるか、を問うのが大学入試です。「常に教科書に立ち返る」。これが受験勉強の正攻法かつ王道なのです。
関連