【JavaScript】定積分の近似値を求める
今回は定積分の近似値を表示するコードを考えてみます。
数IIIの教科書を開くと,定積分を求めるもう一つの方法として区分求積法というものが説明されています。詳しくは教科書を読むとして,区分求積は簡単に言えば関数のグラフを小さな長方形に分割してその和を求めることで積分しようということでした。
区分求積法と定積分
$\displaystyle\lim_{n\rightarrow\infty}\sum_{k=1}^n f(x_k)\Delta x=\int_a^b f(x)\space dx$
ただし,$\Delta x=\cfrac{b-a}{n}$,$x_k=a+k\Delta x$
これを用いて区間 [$a$,$b$] における定積分を行います。
全体のコード
<!DOCTYPE html>
<html>
<body>
<script>
//被積分関数を f(x)として定義する
let f = x => Math.sqrt(3 * x + 2);
//積分の値をS(a,b)として定義する
let S = (a, b) => {
let s = 0; //sに計算結果を積み上げることで積分の値とする
const n = 10 ** 8; //∞の代わりに10の8乗を用いる
const dx = (b - a) / n;
for (let k = 0; k < n; k++) {
const x = a + (k + 1) * dx;
const y = f(x);
s += y * dx; //sに計算結果を積み上げる
}
return s;
};
//直線を描く関数
let drawLine = obj => {
let color, dotted;
switch (obj.style) {
case 'blue':
color = 'blue';
dotted = 0;
break;
case 'greenDotted':
color = 'green';
dotted = 0.1;
break;
case 'Orange':
color = '#FFCC00';
break;
}
document.write('<line x1=' + obj.X1 + ' y1=' + obj.Y1 + ' x2=' + obj.X2 + ' y2=' + obj.Y2 + ' stroke="' + color + '" stroke-width=' + range * 2 + ' stroke-dasharray=' + dotted + ' />');
};
const Range = 10; // x軸両端の幅
const range = Range / 400;
//軸線を描く
document.write('<div><svg width=400 height=400><line x1=0 y1=200 x2=400 y2=200 stroke="black"/><line x1=200 y1=0 x2=200 y2=400 stroke="black"/><g transform="translate(200,200)scale(' + (1 / range) + ', ' + (-1 / range) + ')">');
let a = 2, b = 4; //積分区間を[a,b]とする
let xy = {}; //描画する線の座標などを格納するオブジェクト
let x = -Range / 2;
for (i = 0; i < 400; i++) {
//区間内であれば塗りつぶす
if (x > a && x < b) {
xy = {
X1: x,
Y1: f(x),
X2: x,
Y2: 0,
style: 'Orange'
};
//f(x)の値が実数であれば塗りつぶす
if (isNaN(xy.Y1) == false) drawLine(xy);
}
x += range;
}
x = -Range / 2;
for (i = 0; i < 400; i++) {
xy = {
X1: x,
Y1: f(x),
X2: x + range,
Y2: f(x + range),
style: 'blue'
};
//始点と終点のどちらかが実数であれば直線をひく
if (isNaN(xy.Y1) == false || isNaN(xy.Y2) == false) drawLine(xy);
x += range;
}
xy = { //積分区間の左端を示す直線
X1: a,
Y1: Range / 2,
X2: a,
Y2: -Range / 2,
style: 'greenDotted'
};
drawLine(xy);
xy = { //積分区間の右端を示す直線
X1: b,
Y1: Range / 2,
X2: b,
Y2: -Range / 2,
style: 'greenDotted'
};
drawLine(xy);
document.write('</g></svg></div>'); //タグを閉じる
document.write('<div>区間 [' + a + ', ' + b + '] 面積 ' + S(a, b) + '</div>');
</script>
</body>
</html>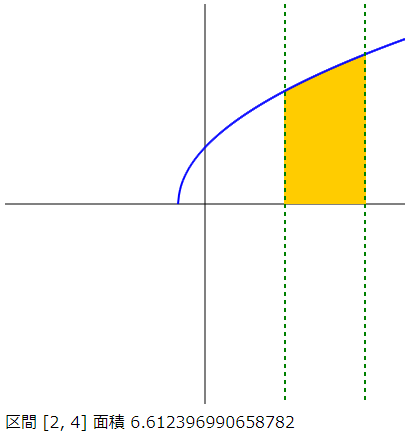
関数の定義
//被積分関数を f(x)として定義する
let f = x => Math.sqrt(3 * x + 2);部分ごとに見ていきます。まず,被積分関数を $f(x)=\sqrt{3x+2}$ として定義します。
//積分の値をS(a,b)として定義する
let S = (a, b) => {
let s = 0; //sに計算結果を積み上げることで積分の値とする
const n = 10 ** 8; //∞の代わりに10の8乗を用いる
const dx = (b - a) / n;
for (let k = 0; k < n; k++) {
const x = a + (k + 1) * dx;
const y = f(x);
s += y * dx; //sに計算結果を積み上げる
}
return s;
};実際に区分計算を行う関数を S(a,b) として定義します。定積分の区間を [a, b] とし,a,b の値を代入すると定積分の近似値を返します。
const n = 10 ** 8; //∞の代わりに10の8乗を用いるもともとは $n\rightarrow\infty$ として極限を求めますが,∞ の代わりに 10 の 8 乗という大きな値を用いて近似値を求めます。数字を大きくするほど近似値の精度は高くなりますが,数が 10 倍になると計算量も 10 倍になるのであまり大きくし過ぎないように注意が必要です。
const dx = (b - a) / n;コード上では $\Delta x$ を dx としています。
for (let k = 0; k < n; k++) {$\displaystyle\sum_{k=1}^n$ は k の値を 1 から n まで変化させながら足し算を行っていくので,for 文を用います。for 文では慣習として k=0 でスタートするので,それに合わせています。上の書き方では,k は 0 から n-1 まで変化していきます。
const x = a + (k + 1) * dx;
const y = f(x);$x_k$ の値を x,$f(x_k)$ の値を y として求めます。さきほど k を 0 から n-1 に変化すると定めたので,k + 1 とすることで k=1 から n までの足し算を行うように帳尻合わせを行っています。
s += y * dx; //sに計算結果を積み上げる縦の長さ y,横の長さ dx の長方形の面積を s に足します。あとは,繰り返しで s に次々と値を足していくことで定積分の結果とします。
return s;最後に計算結果を返します。
switch 文を使う
//直線を描く関数
let drawLine = obj => {
let color, dotted;
switch (obj.style) {
case 'blue':
color = 'blue';
dotted = 0;
break;
case 'greenDotted':
color = 'green';
dotted = 0.1;
break;
case 'Orange':
color = '#FFCC00';
break;
}
document.write('<line x1=' + obj.X1 + ' y1=' + obj.Y1 + ' x2=' + obj.X2 + ' y2=' + obj.Y2 + ' stroke="' + color + '" stroke-width=' + range * 2 + ' stroke-dasharray=' + dotted + ' />');
};
直線をひく関数 drawLine は以前と少し書き方を変えて switch 文を用いています。switch 文は条件によって処理を分けるものです。実際の書き方は上の通りです。
switch (obj.style) は obj.style の内容によって処理を分けることを示しています。obj.style の中にはひこうとする直線のスタイルが入っていて,blue であれば青色の直線をひくという設定を行っています。最後に処理が終わりであることを示す break を書いておきます。ここでは blue (青色の直線),greenDotted (緑色の点線),Orange (オレンジ色の直線) の 3 種類の線が定義されています。
あとで紹介しますが,関数に渡されているオブジェクト obj にはそれ以外にも直線の始点と終点の座標も格納されているので,それらをもとに最後に直線をひいています。
区間を示す直線をひく
let a = 2, b = 4; //積分区間を[a,b]とするまず,区間 [a, b] を定めます。今回は区間 [2, 4] で定積分を行います。
for (i = 0; i < 400; i++) {
//区間内であれば塗りつぶす
if (x > a && x < b) {
xy = {
X1: x,
Y1: f(x),
X2: x,
Y2: 0,
style: 'Orange'
};
//f(x)の値が実数であれば塗りつぶす
if (isNaN(xy.Y1) == false) drawLine(xy);
}
x += range;
}今回は x 軸の幅を 10 で設定しているので,x の値はは -5 から 5 まで変化していきます。
if (x > a && x < b) {これは「x の値が x > a かつ x < b ならば」という意味です。x の値が定積分を行う区間内であれば,その部分を塗りつぶしていきます。
xy = {
X1: x,
Y1: f(x),
X2: x,
Y2: 0,
style: 'Orange'
};上の方でいったん let xy = {}; として,xy がオブジェクトであることを宣言しています。オブジェクトについては以前も紹介しましたが,xy という名前の箱を用意して,その中に X1 や Y1 というラベルを貼った紙を放り込んでいるというイメージです。ここでは x の値が書かれた紙に X1 というラベルを付け,関数 f(x) を計算した値が書かれた紙には Y1 というラベルが付けられています。これよりあとでは,xy.X1 が x の値,xy.Y1 が f(x) の値を示すことになります。
実際の塗りつぶしの作業は,区間 [a, b] において x の値を変化させながら,x 軸から f(x) のグラフまで垂直な直線をひたすらひいていくことで塗りつぶしていきます。
ラベル X1, Y1 は始点の x, y 座標,X2, Y2 は終点の x,y 座標,style の設定 Orange はオレンジ色の直線をひくことを意味しています。
グラフを描く
for (i = 0; i < 400; i++) {
xy = {
X1: x,
Y1: f(x),
X2: x + range,
Y2: f(x + range),
style: 'blue'
};
//始点と終点のどちらかが実数であれば直線をひく
if (isNaN(xy.Y1) == false || isNaN(xy.Y2) == false) drawLine(xy);
x += range;
}$f(x)=\sqrt{3x+2}$ のグラフを描く部分です。終点側の x 座標が x+range となっているのは,終点側の座標を画面上の 1 ピクセル右側にしているということです。
//始点と終点のどちらかが実数であれば直線をひく
if (isNaN(xy.Y1) == false || isNaN(xy.Y2) == false) drawLine(xy);f(x) の値が実数であるかどうかを判定して直線をひきます。$f(x)=\sqrt{3x+2}$ は $x$ < $-\cfrac{2}{3}$ の範囲では虚数となりグラフを描くことができません。isNaN は値が実数であるかどうかを判定するもので,実数でなければ true,実数なら false を返します。ここでは,始点または終点の y 座標が実数であるならば,実際にグラフの直線を描画することにしています。
xy = { //積分区間の左端を示す直線
X1: a,
Y1: Range / 2,
X2: a,
Y2: -Range / 2,
style: 'greenDotted'
};
drawLine(xy);
xy = { //積分区間の右端を示す直線
X1: b,
Y1: Range / 2,
X2: b,
Y2: -Range / 2,
style: 'greenDotted'
};
drawLine(xy);ここは区間の左端と右端を示す垂直な点線をひく部分です。
近似値を表示する
document.write('<div>区間 [' + a + ', ' + b + '] 面積 ' + S(a, b) + '</div>');最後に近似値を表示します。定積分の値はグラフの塗りつぶした部分の面積を表しているので,ここでは面積として値を表示しています。
今回の定積分の近似値は有効数字 6 ケタくらいまでは信頼できる値として考えてよいと思います。f(x) の式を書き換えることでさまざまな関数の定積分の近似値を求めることができるので,いろいろ試してみてください。
SNSでシェア