【JavaScript】媒介変数表示でリサージュ曲線を描く
前回でオブジェクトの説明を終えたので,ここからはオブジェクトを使うことを前提に話を進めていきます。ちなみにこれをオブジェクト指向プログラミングと呼んだりしますが,今となってはオブジェクトを使うのは単に当たり前のことです。
ところで,数III の教科書で極座標などを説明するところの最後にコンピューターで描くグラフとしてリサージュ曲線なるものが紹介されていると思いますが,恐らくみなさんさらっと読み飛ばしていることでしょう。入試に出ない話なのでそれでいいのですが,プログラミングの側から言うと見逃すわけにはいきません。
今回は実際にコードを書いてリサージュ曲線を再現してみましょう。
媒介変数表示で関数を描く
ここでもオブジェクトを使っていきますが,今回のようにやりとりする情報が少ない場合はオブジェクトのありがたみはあまりないかもしれません。
<!DOCTYPE html>
<html>
<body>
<script>
//関数f(x)を定義する
let f = (a, b, t) => {
let obj = {}; //返り値をオブジェクト型として宣言
obj.x = Math.sin(a * t);
obj.y = Math.sin(b * t);
return obj;
};
//直線を描く関数
let drawLine = obj => {
let color, dotted;
if (obj.style == 'blue') {
color = 'blue';
dotted = 0;
}
if (obj.style == 'greenDotted') {
color = 'green';
dotted = 0.1;
}
document.write('<line x1=' + obj.X1 + ' y1=' + obj.Y1 + ' x2=' + obj.X2 + ' y2=' + obj.Y2 + ' stroke="' + color + '" stroke-width=' + range * 2 + ' stroke-dasharray=' + dotted + ' />');
};
const Range = 20; // x軸両端の幅
const range = 0.01;
let t = 0
const a = 4,
b = 5; //リサージュ曲線の形を決める定数
//軸線を描く
document.write('<svg width=400 height=400><line x1=0 y1=200 x2=400 y2=200 stroke="black"/><line x1=200 y1=0 x2=200 y2=400 stroke="black"/><g transform="translate(200,200)scale(' + (1 / range) + ', ' + (-1 / range) + ')">');
//関数のグラフを描く
for (let i = 0; i < 1000; i++) { //処理を1000回繰り返し
let inter1 = f(a, b, t); //直線をひく座標を格納するオブジェクト
let inter2 = f(a, b, t + range);
let xy = {}; //オブジェクトxyを宣言
xy.X1 = inter1.x;
xy.Y1 = inter1.y;
xy.X2 = inter2.x;
xy.Y2 = inter2.y;
xy.style = 'blue';
//始点と終点の座標をもとに直線を引く
drawLine(xy);
t += range; // tの値を次の点の座標にする
}
//最後にタグを閉じる
document.write('</g></svg>');
</script>
</body>
</html>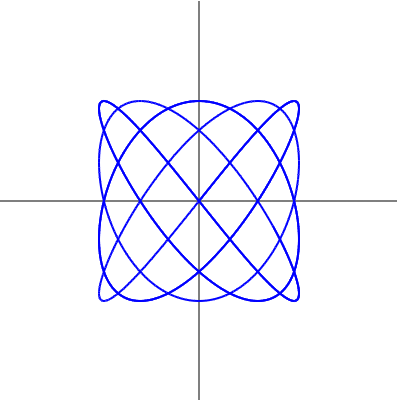
関数の定義
//関数f(x)を定義する
let f = (a, b, t) => {
let obj = {}; //返り値をオブジェクト型として宣言
obj.x = Math.sin(a * t);
obj.y = Math.sin(b * t);
return obj;
};リサージュ曲線は $t$ を媒介変数をして
$x=\sin at$,$y=\sin bt$
と表されます。$a$,$b$ は定数で,今回は $a=4$,$b=5$ とすることで上のようなグラフが描かれます。
let f = (a, b, t) => {関数 f は a, b, t の 3 つの値を受け取ります。
let obj = {}; //返り値をオブジェクト型として宣言
obj.x = Math.sin(a * t);
obj.y = Math.sin(b * t);obj という名前のオブジェクトを用意します。前回話しましたが,obj という名前の箱を用意して,そこに x,y と書いたラベルを貼った紙を放り込んでいくわけです。それぞれの紙には三角関数 sin の計算結果が書かれています。
今回は箱の中に紙が 2 枚しかないので,わざわざ箱に入れるには微妙な感じかもしれません。
return obj;x,y座標を求めた紙にラベルを付け,箱の中に放り込んだあと,その箱を渡します。
媒介変数表示のグラフを描く
//関数のグラフを描く
for (let i = 0; i < 1000; i++) { //処理を1000回繰り返し
let inter1 = f(a, b, t); //直線をひく座標を格納するオブジェクト
let inter2 = f(a, b, t + range);
let xy = {}; //オブジェクトxyを宣言
xy.X1 = inter1.x;
xy.Y1 = inter1.y;
xy.X2 = inter2.x;
xy.Y2 = inter2.y;
xy.style = 'blue';
//始点と終点の座標をもとに直線を引く
drawLine(xy);
t += range; // tの値を次の点の座標にする
}ここでは,t の値を変化させて直線をひいています。オブジェクト inter1 に f が導出した始点の x,y 座標を格納し,inter2 には直線の終点の座標を格納します。そのあと,オブジェクト xy を用意して始点と終点の座標を格納し,関数 drawLine に値を渡します。
定数 a,b の値を変えることでさまざまな曲線を描くことができるので試してみましょう。
SNSでシェア