【JavaScript】オブジェクトで情報をまとめる
前回までで関数のグラフと漸近線を描くことができるようになりました。とはいえ,y 軸に平行な漸近線の描きかたがかなりムリヤリだったので今回はもう少し数学的に改善します。
また,はじめのころは関数は y の値を求めるだけだったのですが,微分係数を求めたり,漸近線の判定などを付け加えるうちにコードがごちゃごちゃになって何をやっているのが分かりにくくなってきました。このままコードにさらに新しい機能を追加していけば迷路になってしまいそうです。
そこで今回はオブジェクトを用いて情報を整理していきます。
漸近線判定の改善
関数 y = f(x) が y 軸に平行な漸近線をもつとき,漸近線の部分で y の値は +∞ か ー∞ に発散します。第二次導関数 y” を考えると,漸近線の手前では y’ と y” がどちらもプラスになるかマイナスになります。また,漸近線に近づくほど y” は大きな正の値が負の値をとるので,それを漸近線の判定条件とします。
(ただし,この条件では $y=x^3$ のグラフのように $x\rightarrow+\infty$ で $y$ が +∞ に発散する場合でも,あるポイントで「漸近線あり」の判定をしてしまうことになります。)
if (gd(x) < -1 && gdd(x) < -1000) {実際の条件式としては上のようにしています。gd(x) は関数を微分した式,gdd(x) はそれをさらに微分した第二次導関数です。微分係数が -1 未満かつ第二次導関数が -1000 未満であれば -∞ であるということにしています。同様にして+∞も判定します。
オブジェクト
これまで,関数 f(x) についてさまざまな情報が追加されバラバラの状態でした。これらをオブジェクトを用いてなるべくまとめていきます。
オブジェクトとは何か,ということを言い出すと途端に抽象的な話になってしまうので,概念の理解はあと回しにしてまずは実際の使い方を理解しましょう。
//関数f(x)を定義する
let f = x => {
//描画するグラフをg(x)として定義
let g = x => (x ** 3 + x ** 2 + 2 * x) / ((2 * x + 1) * (x - 3));
//g(x)の微分係数gd(x)を定義
let gd = x => {
let yd = (g(x + h) - g(x)) / h;
//ydが計算不能なときは代わりに0に近い小さな値を返す
if (isNaN(yd) == true) yd = 0.0001;
return yd;
}
//g(x)の第二次導関数gdd(x)を定義
let gdd = x => (gd(x + h) - gd(x)) / h;
let obj = {}; //返り値をオブジェクト型として宣言
obj.value = g(x);
obj.yd = gd(x);
obj.ydd = gdd(x);
return obj;
};
let y1 = f(x);
let y2 = f(x + range);上はコードの一部を抜粋したものです。これまでなら,最後の行の y1 = f(x) で y1 に一つの値が代入されました。しかし,ここでは f(x) はオブジェクトを返しているので,y1 に複数の値をもつオブジェクトというものが格納されます。
処理の流れとしては,まず関数 f(x) の中にさらに g(x),gd(x),gdd(x) を定義しています。それぞれ y,y’,y” に相当します。そのあと,let obj = {}; で obj という名前のオブジェクトを宣言します。宣言とはコンピューターに「ここから obj をオブジェクトとして扱いますよ。」と教えることです。
obj.value = g(x);
obj.yd = gd(x);
obj.ydd = gdd(x);ここはオブジェクトに値を格納していく部分です。
ざっくり説明してみます。まず,箱と付箋,紙を用意します。g(x)は具体的には $y=\cfrac{x^3+x^2+2x}{(2x+1)(x-3)}$ という計算式であり,紙の上で計算を行って結果を求めます。また,この紙に value と書いた付箋を貼っておきます(これをラベルと言います)。そして,付箋を貼った紙を obj と名前が書かれた箱の中に放り込みます。
あとは同様に,y’ を求めた紙に yd,y” を求めた紙に ydd というラベルを付けて同じ箱の中に放り込んでいきます。
return obj;ここで obj という箱を結果として返しています。
これまで関数 f(x) は x の値によって一つの値を返してきましたが,今度は計算結果が書かれた紙を何枚も放り込んだ箱を返してくるようになります。
したがって f(x) はもはや関数というより,計算結果を詰め込んだ箱を持ってくるロボットのようなものだとイメージしたほうが良いでしょう。
let y1 = f(x);
let y2 = f(x + range);この行で,y1 と y2 というオブジェクトに f(x) を格納しています。
つまりこういうことです。コンピューターがこの行を読むと,f というロボットに「x の値は~だから,結果持ってきて。」と指示を出します。指示されたロボット f は計算を行い,3 枚の紙に y,y’,y” の値をそれぞれ書き込み,ラベルを貼った上で obj という箱に放り込み,コンピューターに渡します。コンピューターは箱から紙を取り出して y1 という箱の中に入れます。これで計算結果の受け渡しが完了しました。
これ以降では,y1.value が y,y1.yd が y’,y1.ydd が y” を表すようになります。
y2 についても同様です。今度はロボット f に x+range という値を渡して,ロボットが持ってきた計算結果を y2 という箱の中に入れるわけです。
今回のコードでは,始点と終点の座標を用いて直線をひくので,y1 に始点の y 座標などの値,y2 に終点の y 座標などの値を格納します。
こうしてみてみると,y1 や y2 は実際に使用する計算結果を入れる箱で,obj はロボット f が結果を渡すまでに自分で使い回している箱だと言えます。
オブジェクト f(x)
<!DOCTYPE html>
<html>
<body>
<script>
//関数f(x)を定義する
let f = x => {
//描画するグラフをg(x)として定義
let g = x => (x ** 3 + x ** 2 + 2 * x) / ((2 * x + 1) * (x - 3));
//g(x)の微分係数gd(x)を定義
let gd = x => {
let yd = (g(x + h) - g(x)) / h;
//ydが計算不能なときは代わりに0に近い小さな値を返す
if (isNaN(yd) == true) yd = 0.0001;
return yd;
}
//g(x)の第二次導関数gdd(x)を定義
let gdd = x => (gd(x + h) - gd(x)) / h;
let obj = {}; //返り値をオブジェクト型として宣言
obj.value = g(x);
obj.yd = gd(x);
obj.ydd = gdd(x);
//微分係数が負で第二次導関数が大きな負の値なら-∞と判断
if (gd(x) < -1 && gdd(x) < -1000) {
obj.yAsym = true;
obj.value = -1000;
}
//微分係数が正で第二次導関数が大きな正の値なら+∞と判断
if (gd(x) > 1 && gdd(x) > 1000) {
obj.yAsym = true;
obj.value = 1000;
}
//ax+b型漸近線の判定
let m = 1000,
n = 1001; //∞の代わりにある大きな値を設定する
//g(m)とg(n)の微分係数がほとんど同じであればそれを漸近線の傾きであると判定
if (Math.abs(gd(m) - gd(n)) < 0.001) {
obj.gAsym = true;
//x=mにおける微分係数を漸近線の傾きとして返す
obj.gradient = gd(m);
//gd(m)*(x-m)+g(m)=gd(m)*x-gd(m)*m+g(m)より切片は-gd(m)*m+g(m)
obj.intercept = -gd(m) * m + g(m);
}
if (Math.abs(gd(-m) - gd(-n)) < 0.001) {
obj.gAsym = true;
//x=mにおける微分係数を漸近線の傾きとして返す
obj.gradient = gd(-m);
//gd(-m)*(x+m)+g(-m)=gd(-m)*x+gd(-m)*m+g(-m)より切片はgd(-m)*m+g(-m)
obj.intercept = gd(-m) * m + g(-m);
}
return obj;
};
//直線を描く関数
let drawLine = obj => {
let color, dotted;
if (obj.style == 'blue') {
color = 'blue';
dotted = 0;
}
if (obj.style == 'greenDotted') {
color = 'green';
dotted = 0.1;
}
document.write('<line x1=' + obj.X1 + ' y1=' + obj.Y1 + ' x2=' + obj.X2 + ' y2=' + obj.Y2 + ' stroke="' + color + '" stroke-width=' + range * 2 + ' stroke-dasharray=' + dotted + ' />');
};
const Range = 20; // x軸両端の幅
const range = Range / 400;
let x = -Range / 2; //始点のx座標
const h = range / 100; // 1/∞の代わりに0に近い小さな値を設定する
//軸線を描く
document.write('<svg width=400 height=400><line x1=0 y1=200 x2=400 y2=200 stroke="black"/><line x1=200 y1=0 x2=200 y2=400 stroke="black"/><g transform="translate(200,200)scale(' + (1 / range) + ', ' + (-1 / range) + ')">');
//関数のグラフを描く
for (let i = 0; i < 400; i++) { //処理を400回繰り返し
let y1 = f(x);
let y2 = f(x + range);
let xy = {}; //直線をひく座標を格納するオブジェクトを宣言
xy.X1 = x;
xy.Y1 = y1.value;
xy.X2 = x + range;
xy.Y2 = y2.value;
xy.style = 'blue';
//始点と終点の座標をもとに直線を引く
if (y1.yAsym == true && y2.yAsym != true) {
//y軸平行漸近線をひく
xy.X1 = x;
xy.Y1 = -Range / 2;
xy.X2 = x;
xy.Y2 = Range / 2;
xy.style = 'greenDotted';
drawLine(xy);
} else {
//グラフを描く
drawLine(xy);
}
x += range; // xの値を次の点の座標にする
}
//ax+b型漸近線をひく
let y = f(0);
if (y.gAsym == true) {
let xy = {};
xy.X1 = -Range / 2;
xy.Y1 = -y.gradient * Range / 2 + y.intercept;
xy.X2 = Range / 2;
xy.Y2 = y.gradient * Range / 2 + y.intercept;
xy.style = 'greenDotted';
drawLine(xy);
}
//最後にタグを閉じる
document.write('</g></svg>');
</script>
</body>
</html>
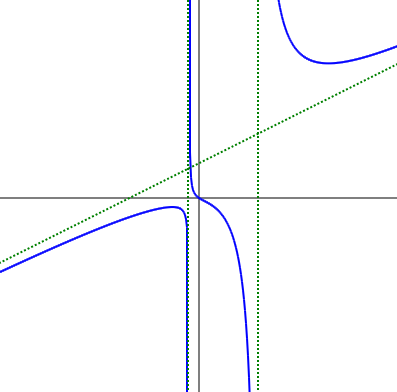
全体のコードは上のようになります。順番に見ていきます。
//関数f(x)を定義する
let f = x => {
//描画するグラフをg(x)として定義
let g = x => (x ** 3 + x ** 2 + 2 * x) / ((2 * x + 1) * (x - 3));
//g(x)の微分係数gd(x)を定義
let gd = x => {
let yd = (g(x + h) - g(x)) / h;
//ydが計算不能なときは代わりに0に近い小さな値を返す
if (isNaN(yd) == true) yd = 0.0001;
return yd;
}
//g(x)の第二次導関数gdd(x)を定義
let gdd = x => (gd(x + h) - gd(x)) / h;
let obj = {}; //返り値をオブジェクト型として宣言
obj.value = g(x);
obj.yd = gd(x);
obj.ydd = gdd(x);ここは上で説明した通りです。$g(x)=\cfrac{x^3+x^2+2x}{(2x+1)(x-3)}$ として,g(x) の微分したものを gd(x),第二次導関数を gdd(x) として,それぞれ value, yd, ydd というラベルを付けてオブジェクトに格納します。
//微分係数が負で第二次導関数が大きな負の値なら-∞と判断
if (gd(x) < -1 && gdd(x) < -1000) {
obj.yAsym = true;
obj.value = -1000;
}
//微分係数が正で第二次導関数が大きな正の値なら+∞と判断
if (gd(x) > 1 && gdd(x) > 1000) {
obj.yAsym = true;
obj.value = 1000;
}y 軸に平行な漸近線を判定します。x の値によってここが漸近線だと判断すると,yAsym というラベルに true という一種の値のようなものを格納します。あとからこのラベルを参照すれば,x の値によってそこが漸近線かどうかを判断できるようになります。また,$y$ の値に∞を代入することはできないので,代わりに 1000 という大きな値を代入します。
//ax+b型漸近線の判定
let m = 1000,
n = 1001; //∞の代わりにある大きな値を設定する
//g(m)とg(n)の微分係数がほとんど同じであればそれを漸近線の傾きであると判定
if (Math.abs(gd(m) - gd(n)) < 0.001) {
obj.gAsym = true;
//x=mにおける微分係数を漸近線の傾きとして返す
obj.gradient = gd(m);
//gd(m)*(x-m)+g(m)=gd(m)*x-gd(m)*m+g(m)より切片は-gd(m)*m+g(m)
obj.intercept = -gd(m) * m + g(m);
}次に斜めにひく ax+b 型の漸近線を判定します。この部分は f(x) の x の値とは無関係に結果を返してきます。本当はこの部分を何度も実行するのはムダなので改善の余地が残ります。
ここでは式が $x\overrightarrow\infty$ で ax+b 型の漸近線を持つとき,gAsym というラベルが true になり,ラベル gradient に直線の傾き,intercept に切片を返します。
if (Math.abs(gd(-m) - gd(-n)) < 0.001) {
obj.gAsym = true;
//x=mにおける微分係数を漸近線の傾きとして返す
obj.gradient = gd(-m);
//gd(-m)*(x+m)+g(-m)=gd(-m)*x+gd(-m)*m+g(-m)より切片はgd(-m)*m+g(-m)
obj.intercept = gd(-m) * m + g(-m);
}上と同様に今度は $x\overrightarrow-\infty$ の場合で,漸近線を判定しています。
return obj;
};最後にオブジェクト obj を返すことで,ここまででラベルを付けた情報をまとめて渡すようにしています。
直線をひく関数
//直線を描く関数
let drawLine = obj => {
let color, dotted;
if (obj.style == 'blue') {
color = 'blue';
dotted = 0;
}
if (obj.style == 'greenDotted') {
color = 'green';
dotted = 0.1;
}
document.write('<line x1=' + obj.X1 + ' y1=' + obj.Y1 + ' x2=' + obj.X2 + ' y2=' + obj.Y2 + ' stroke="' + color + '" stroke-width=' + range * 2 + ' stroke-dasharray=' + dotted + ' />');
};これまで直線をひくときは <line /> と使って直接ひいていましたが,<line /> に与える情報が複雑になってきて分かりにくいので,関数として分離しています。
ここで関数に渡す値もオブジェクトにしています。ラベル X1,Y1 が始点,X2, Y2 が終点の座標,style は線の種類を表し,blue で青線,greenDotted で緑色の点線としています。
直線をひくときにもいくつもの情報が必要なので,オブジェクトという箱の中に情報をひとまとめにして drawLine という名前の直線をひくロボットにいっぺんに渡してしまおうというわけです。
情報を受け取ったロボット drawline は箱から style を取り出して,線の色と線種を決め,<line /> を使って実際に直線をひいています。
グラフを描く
//軸線を描く
document.write('<svg width=400 height=400><line x1=0 y1=200 x2=400 y2=200 stroke="black"/><line x1=200 y1=0 x2=200 y2=400 stroke="black"/><g transform="translate(200,200)scale(' + (1 / range) + ', ' + (-1 / range) + ')">');
//関数のグラフを描く
for (let i = 0; i < 400; i++) { //処理を400回繰り返し
let y1 = f(x);
let y2 = f(x + range);
let xy = {}; //直線をひく座標を格納するオブジェクトを宣言
xy.X1 = x;
xy.Y1 = y1.value;
xy.X2 = x + range;
xy.Y2 = y2.value;
xy.style = 'blue';
//始点と終点の座標をもとに直線を引く
if (y1.yAsym == true && y2.yAsym != true) {
//y軸平行漸近線をひく
xy.X1 = x;
xy.Y1 = -Range / 2;
xy.X2 = x;
xy.Y2 = Range / 2;
xy.style = 'greenDotted';
drawLine(xy);
} else {
//グラフを描く
drawLine(xy);
}
x += range; // xの値を次の点の座標にする
}ここで,軸線を描いたあとにグラフを描きます。y1,y2 でオブジェクトを受け取ったあと,今度は xy という直線をひくための新しいオブジェクトを用意しています。
xy.X1 = x;
xy.Y1 = y1.value;
xy.X2 = x + range;
xy.Y2 = y2.value;
xy.style = 'blue';この部分で,直線をひくのに必要な情報を X1 や Y1 などのラベルをつけて xy というオブジェクトに放り込んでいきます。
//始点と終点の座標をもとに直線を引く
if (y1.yAsym == true && y2.yAsym != true) {ラベル yAsym には関数の値を求めたポイントにおいて値が+∞や-∞に発散しているかどうかの情報が入っていました。そのポイントが漸近線であれば true を返してきます。
実際にはオブジェクト f は計算誤差のせいで漸近線の前後で 2,3 箇所 true を返してきます。そこでつじつま合わせとして次のポイントが漸近線ではないときだけ漸近線をひくことにしています。こうすれば漸近線 2,3 箇所のうち最後の 1 箇所だけ漸近線がひかれます。
//y軸平行漸近線をひく
xy.X1 = x;
xy.Y1 = -Range / 2;
xy.X2 = x;
xy.Y2 = Range / 2;
xy.style = 'greenDotted';
drawLine(xy);
} else {
//グラフを描く
drawLine(xy);
}
x += range; // xの値を次の点の座標にする
}そのあと,情報を漸近線のものに書き換えて drawLine に送ります。
drawLine(xy);このように情報をオブジェクトにまとめておくと,実際に送るときの書き方は極めてシンプルで,オブジェクトの名前だけを書けばよいのです。
イメージとしては直線をひくロボット drawLine に xy と書かれた箱を箱ごと渡して「あとはよろしく!」という感じでしょうか。
そのあと else の部分は漸近線はないとき,つまりグラフを描くことになるので,もともと設定していた xy をそのまま渡しています。
//ax+b型漸近線をひく
let y = f(0);
if (y.gAsym == true) {
let xy = {};
xy.X1 = -Range / 2;
xy.Y1 = -y.gradient * Range / 2 + y.intercept;
xy.X2 = Range / 2;
xy.Y2 = y.gradient * Range / 2 + y.intercept;
xy.style = 'greenDotted';
drawLine(xy);
}最後は ax+b 型の漸近線を描く部分です。ここでは,f(x) に放り込む値が何であろうが返ってくる結果は同じなので x=0 として,オブジェクト y に結果を受け取ることにしています。
ラベル gAsym は関数が ax+b 型漸近線をもつとき true を返します。したがって if 文でそれを判定し true なら,オブジェクト xy に直線をひくための情報を格納し drawLine に渡しています。
というわけで今回はオブジェクトの話でした。箱に情報を詰め込んで箱ごと相手に渡すイメージができあがれば,大量のデータを処理するための道筋が開けそうです。
SNSでシェア