【JavaScript】二次関数のグラフを描いてみる

公開日:2020/05/17

最終更新日:2020/05/17

今回は画面上に二次関数のグラフを描いてみましょう。見栄えのよいグラフを描くためには色々な技術が必要になるので，初めはその部分は手を出さずにできるだけシンプルに話を進めたいと思います。

プログラムの動かし方

用いる言語は HTML と Javascript です。ソースコードをコピーしてメモ帳などに貼り付け→test.html など HTML形式のファイルとして保存→エクスプローラーで保存したファイルをダブルクリック→ブラウザが起動して結果を表示。

直線を描く

直線を描いてみましょう。

<!DOCTYPE html><html><body>

<svg width=100 height=100>
  <line x1=0 y1=0 x2=100 y2=100 stroke="black"/>
</svg>

</body></html>

次に直線をひきます。

  <line x1=0 y1=0 x2=100 y2=100 stroke="black"/>

細かい文法は後回しにしてまずは使ってみることが大事です。この文は座標(0，0)と(100,100)の間に直線を引くという意味です。数字を変えれば様々な直線が引けます。

実際に座標を入れてみると分かりますが，コンピューターでは左上のほうが原点(0，0)になります。数学では左下を原点(0，0)とするので注意が必要です。この問題はあとで調節します。

軸線を用意する

ここからグラフを描いてみます。まず，グラフの位置関係を分かりやすくするために $x$ 軸と$y$ 軸を用意します。描画領域の大きさは幅 400，高さ 400 とします。

<!DOCTYPE html><html><body>

<svg width=400 height=400>
    <line x1=0 y1=200 x2=400 y2=200 stroke="black" />
    <line X1=200 y1=0 x2=200 y2=400 stroke="black" />
</svg>

</body></html>

軸線が描かれました。

グラフ上に直線を描く

ここから Javascript を使っていきます。

<!DOCTYPE html><html><body><script>

  document.write('<svg width=400 height=400>');
  document.write('<line x1=0 y1=200 x2=400 y2=200 stroke="black" /><line x1=200 y1=0 x2=200 y2=400 stroke="black" />');
  document.write('<line x1=0 y1=0 x2=200 y2=200 stroke="blue" transform="translate(200,200)scale(1,-1)" />');
  document.write('</svg>');

</script></body></html>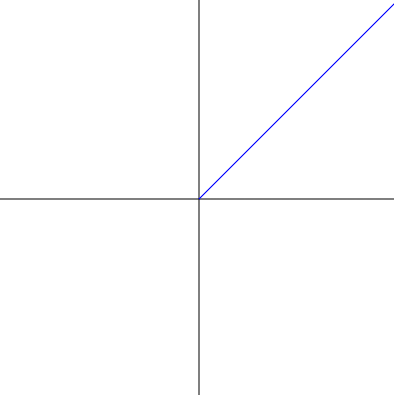

document.write は画面に文字を書く命令です。今回のように文字の代わりにタグを書けば，タグに沿って図形を描くこともできます。

  document.write('<line x1=0 y1=0 x2=200 y2=200 stroke="blue" transform="translate(200,200)scale(1,-1)" />');

直線を描く命令文が少し複雑になりました。座標(0，0)から(200，200)へ直線を引いています。transform = “translate(200,200)scale(1,-1)” は原点を(200,200)の位置にして $y$ 軸を上下反対にするということです。もともと描画領域の原点は左上ですが，こうすることで軸が交差している描画領域の中心を原点とし，上向きの座標をプラスとすることができます。

ここからもう少し調整します。

<!DOCTYPE html><html><body><script>

  document.write('<svg width=400 height=400><line x1=0 y1=200 x2=400 y2=200 stroke="black"/><line x1=200 y1=0 x2=200 y2=400 stroke="black"/>');
  document.write('<g transform="translate(200,200)scale(40,-40)"><line x1=0 y1=0 x2=5 y2=5 stroke="blue" stroke-width="0.05"/></g>');
  document.write('</svg>');

</script></body></html>

命令文がさらに複雑になりましたが，中身を見ていきましょう。この文は<line>タグを<g>～</g>で囲む構造になっています。<g>タグに描画のためのいろいろな要素を書いておくことで，タグの間に書かれた直線にすべて同じ設定を用いることができます。scaleの値を 1 から 40 に変えることで，縮尺が 40 倍になります。もともと領域の右上の座標は(200，200)でしたが，200÷40=5 だから，(5，5)になります。また， stroke-width=”0.05″ は線の太さを 0.05 にするということです。グラフが見やすいように数字をいろいろと変えてみると良いでしょう。

2次関数のグラフを描く

$y=ax^2+b$ のグラフを描いてみましょう。いくつかの短い直線をつなげていくことで見た目が曲線になるように描いていきます。

<!DOCTYPE html><html><body><script>

document.write('<svg width=400 height=400>');
document.write('<line x1=0 y1=200 x2=400 y2=200 stroke="black" /><line x1=200 y1=0 x2=200 y2=400 stroke="black" />');

let x1 =-5, y1, x2, y2;
let a = 1, b = 0; // y=ax^2+b の a,b の値

for(let i = 0; i < 10; i++) { //処理を10回繰り返し

  y1 = a * x1 * x1 + b;    //始点のy座標を求める

  //始点のx座標より1大きい値を終点のx座標とする
  x2 = x1 + 1;
  y2 = a * x2 * x2 + b;    //終点のy座標を求める

  //始点と終点の座標をもとに直線を引く
  document.write('<g transform="translate(200,200)scale(40,-40)"><line x1='+x1+' y1='+y1+' x2='+x2+' y2='+y2+' stroke="blue" stroke-width="0.05"/></g>');

  x1 = x2;    //終点のx座標を次の始点のx座標とする

};

document.write('</svg>');

</script></body></html>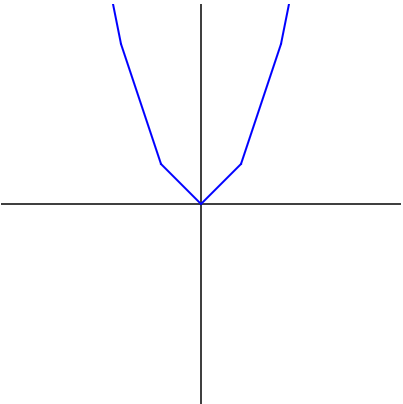

$y=x^2$ のグラフが描かれましたが，曲線がカクカクです。ここでは $x$ の値を $-5$ から $5$ まで 1 ずつ変化させてグラフを描いたので，このようになります。では，グラフをもっと細かくしていきましょう。

<!DOCTYPE html><html><body><script>

document.write('<svg width=400 height=400>');
document.write('<line x1=0 y1=200 x2=400 y2=200 stroke="black" /><line x1=200 y1=0 x2=200 y2=400 stroke="black" />');

let x1 = -5, y1, x2, y2;
let a = 1, b = 0; // y=ax^2+b の a,b の値

for(let i=0; i < 100; i++) { //処理を100回繰り返し

  y1 = a * x1 * x1 + b;    //始点のy座標を求める
  //始点のx座標より0.1大きい値を終点のx座標とする
  x2 = x1 + 0.1;
  y2 = a * x2 * x2 + b;    //終点のy座標を求める

  //始点と終点の座標をもとに直線を引く
  document.write('<g transform="translate(200,200)scale(40,-40)"><line x1='+x1+' y1='+y1+' x2='+x2+' y2='+y2+' stroke="blue" stroke-width="0.05"/></g>');

  x1 = x2;    //終点のx座標を次の始点のx座標とする

};

document.write('</svg>');

</script></body></html>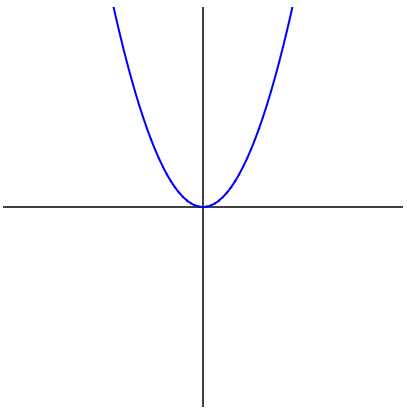

今度は $x$ の変位を 0.1 ずつとしたのでなめらかな二次関数のグラフが出来上がりました。