【JavaScript】フラクタルを描く

公開日:2020/05/19

最終更新日:2023/01/06

今回はいかにもコンピューターグラフィックスらしいグラフということで，フラクタル図形を描画してみましょう。

<!DOCTYPE html><html lang=“ja”><body><script>

const range = 2.2; // x軸両端の幅
let x = -range/2; //始点のx座標

//軸線を描く
document.write('<svg width=400 height=400><line x1=0 y1=200 x2=400 y2=200 stroke="black"/><line x1=200 y1=0 x2=200 y2=400 stroke="black"/>');

//始めの三角形の座標を格納する
//x座標を格納する配列
let Ux = [-Math.sqrt(3)/2, Math.sqrt(3)/2, 0, -Math.sqrt(3)/2];

//y座標を格納する配列
let Uy = [-0.5, -0.5, 1, -0.5];

for(let j = 0; j < 3; j++) {

  //新しい座標を格納する配列
  let Tx = [];
  let Ty = [];

  for (let i = 0; i < Ux.length -1; i++) {

    const Ax = Ux[i]; //点Aの座標を代入
    const Ay = Uy[i];

    const Bx = Ux[i+1]; //点Bの座標を代入
    const By = Uy[i+1];

    const Cx = 2/3*Ax+1/3*Bx; //点Cの座標を代入
    const Cy = 2/3*Ay+1/3*By;

    const Dx = 1/2*(Ax+Bx)+Math.sqrt(3)/6*(By-Ay); //点Dの座標を代入
    const Dy = 1/2*(Ay+By)+Math.sqrt(3)/6*(Ax-Bx);

    const Ex = 1/3*Ax+2/3*Bx; //点Eの座標を代入
    const Ey = 1/3*Ay+2/3*By;

    //新しい座標をTxに格納する
    Tx.push(Ax, Cx, Dx, Ex, Bx);
    Ty.push(Ay, Cy, Dy, Ey, By);

  };

  //Txの内容をUxに代入する
  Ux = Array.from(Tx);
  Uy = Array.from(Ty);

};

//グラフを描く
for (let i = 0; i < Ux.length - 1; i++) {

  document.write('<g transform="translate(200,200)scale('+(400/range)+', '+(-400/range)+')">');

  document.write('<line x1='+Ux[i]+' y1='+Uy[i]+' x2='+Ux[i+1]+' y2='+Uy[i+1]+' stroke="black" stroke-width='+range/400*1+' />');

  document.write('</g>');

};

//最後にタグを閉じる
document.write('</svg>');

</script></body></html>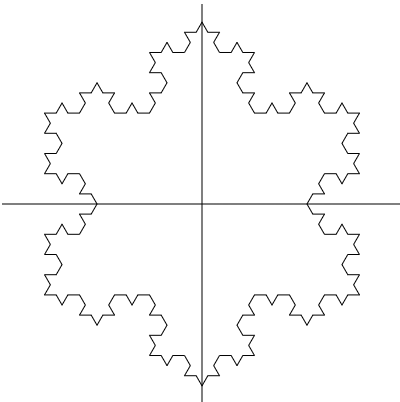

フラクタルの仕組み

今回のフラクタルは初めに正三角形を用意して，それぞれの辺の上に新しい正三角形を作ることによってできあがります。この作業を繰り返していくことで，どんどん複雑な図形になっていきます。

法線ベクトルで座標を求める

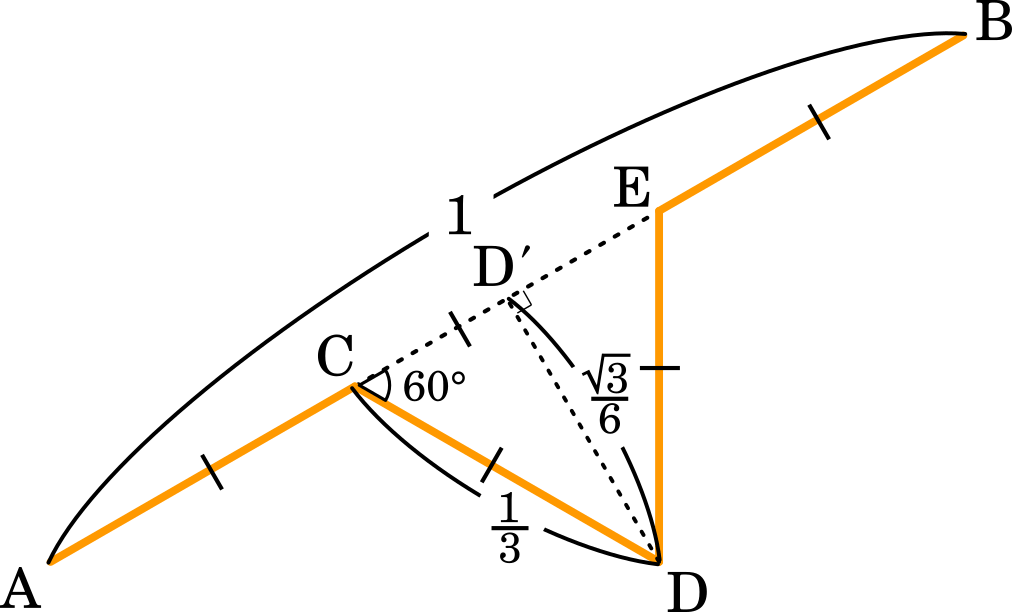
それぞれの辺に新しい正三角形を付け加えるためにはいくつか新しい点を追加する必要があります。もともとの正三角形の 1 つの辺を AB とし，AB を 3 等分した点をそれぞれ C，E とします。また，AB の中点を D’ として，D’ から AB に垂直な直線 D’D をひきます。このとき CD’ : CD : D’D = $1:2:\sqrt{3}$ の関係が成り立つので，AB : D’D = $1:\cfrac{\sqrt{3}}{6}$ となります。

それぞれの点の座標を A(Ax，Ay)，B(Bx，By)，・・・として，点C，D，E の座標を求めていきましょう。

このとき，数IIBで習うベクトルを用いると効率よく座標を求めることができます。

点 C は直線 AB を 1 : 2 で内分する点だから

$\overrightarrow{\text{OC}}=\cfrac{2\overrightarrow{\text{OA}}+\overrightarrow{\text{OB}}}{1+2}=\cfrac{2}{3}\overrightarrow{\text{OA}}+\cfrac{1}{3}\overrightarrow{\text{OB}}$

また，点 E は直線 AB を 2 : 1 で内分する点だから

$\overrightarrow{\text{OE}}=\cfrac{\overrightarrow{\text{OA}}+2\overrightarrow{\text{OB}}}{2+1}=\cfrac{1}{3}\overrightarrow{\text{OA}}+\cfrac{2}{3}\overrightarrow{\text{OB}}$

$x$，$y$ 座標をそれぞれ求めると

$Cx=\cfrac{2}{3}Ax+\cfrac{1}{3}Bx$，$Cy=\cfrac{2}{3}Ay+\cfrac{1}{3}By$

$Ex=\cfrac{1}{3}Ax+\cfrac{2}{3}Bx$，$Ey=\cfrac{1}{3}Ay+\cfrac{2}{3}By$

点 D を求めるには法線ベクトルを用いると良いです。法線ベクトルとは，あるベクトルに垂直なベクトルということです。ここでは $\overrightarrow{\text{AB}}$ に対して垂直な法線ベクトルを $\vec{n}$ とします。

ここで，ある直線の傾きが $\cfrac{b}{a}$ だったとして，それに垂直な直線の傾きは $-\cfrac{a}{b}$ となりました。つまり $a$ と $b$ を入れ替えて符号を反対にすれば良いということです。同じように $\vec{p}=(a,b)$ の法線ベクトルは $\vec{n}=(b,-a)$ と表すことができます。

$\overrightarrow{\text{AB}}=(Bx-Ax,By-Ay)$ より，法線ベクトルは $\vec{n}=(By-Ay,-Bx+Ax)$

$\vec{n}$ の長さは $\overrightarrow{\text{AB}}$ の長さと同じです。よって

$\overrightarrow{\text{D’D}}=\cfrac{\sqrt{3}}{6}\vec{n}$

また点D’ は AB の中点だから $\overrightarrow{\text{OD’}}=\cfrac{1}{2}(\overrightarrow{\text{OA}}+\overrightarrow{\text{OB}})$

これらを用いて $\overrightarrow{\text{OD}}$ は

$\overrightarrow{\text{OD}}=\overrightarrow{\text{OD’}}+\overrightarrow{\text{D’D}}$

$=\cfrac{1}{2}(\overrightarrow{\text{OA}}+\overrightarrow{\text{OB}})+\cfrac{\sqrt{3}}{6}\vec{n}$

点 D の $x$，$y$ 座標をそれぞれ求めると

$Dx=\cfrac{1}{2}(Ax+Bx)+\cfrac{\sqrt{3}}{6}(By-Ay)$

$Dy=\cfrac{1}{2}(Ay+By)+\cfrac{\sqrt{3}}{6}(Bx-Ax)$

これで，すべての点の座標が求められました。

最初の正三角形の座標を決める

//始めの三角形の座標を格納する
//x座標を格納する配列
let Ux = [-Math.sqrt(3)/2, Math.sqrt(3)/2, 0, -Math.sqrt(3)/2];

//y座標を格納する配列
let Uy = [-0.5, -0.5, 1, -0.5];

スタート地点となる正三角形の $x$，$y$ 座標を，それぞれ Ux，Uy という配列に格納します。Math.sqrt(3)/2 は $\cfrac{\sqrt{3}}{2}$ のことです。また，最後にひく直線はスタート地点に戻らないといけないので，配列の最後に最初と同じ座標を格納します。

繰り返し計算で新しい点の座標を求める

for(let j = 0; j < 3; j++) {

ここの 3 がフラクタルの繰り返し回数を決めている部分です。0 にすると正三角形のみ描かれます。

  //新しい座標を格納する配列
  let Tx = [];
  let Ty = [];

はじめの正三角形の座標に新しい点の座標を加え，それらの $x$，$y$ 座標を配列 Tx，Ty に格納していきます。

  for (let i = 0; i < Ux.length -1; i++) {

    const Ax = Ux[i]; //点Aの座標を代入
    const Ay = Uy[i];

    const Bx = Ux[i+1]; //点Bの座標を代入
    const By = Uy[i+1];

    const Cx = 2/3*Ax+1/3*Bx; //点Cの座標を代入
    const Cy = 2/3*Ay+1/3*By;

    const Dx = 1/2*(Ax+Bx)+Math.sqrt(3)/6*(By-Ay); //点Dの座標を代入
    const Dy = 1/2*(Ay+By)+Math.sqrt(3)/6*(Ax-Bx);

    const Ex = 1/3*Ax+2/3*Bx; //点Eの座標を代入
    const Ey = 1/3*Ay+2/3*By;

    //新しい座標をTxに格納する
    Tx.push(Ax, Cx, Dx, Ex, Bx);
    Ty.push(Ay, Cy, Dy, Ey, By);

  };

ここでは for ～を用いて図形の辺の数だけ処理を繰り返しています。Ux.length は配列 Ux に格納されている要素の個数を表します。はじめの正三角形では値を 4 つ格納したので，Ux.length - 1 = 3 です。

あとは上で行ったベクトルの計算に基づいて点 A ～ E の座標を代入していきます。そして，新しくできた図形の $x$，$y$ 座標はそれぞれ配列 Tx，Ty に追加していきます。ここでは push() を用いて，点 A，C，D，E，B の 5 つの座標を配列の最後に追加しています。

  //Txの内容をUxに代入する
  Ux = Array.from(Tx);
  Uy = Array.from(Ty);

すべての辺において新しい点の座標を求めたら，その内容を配列 Ux，Uy に戻します。そしてループが最初に戻った時，再び Ux，Uy をもとにしてさらに計算をしていくことになるのです。Array.from() は配列の内容をコピーする関数です。

グラフの描画

//グラフを描く
for (let i = 0; i < Ux.length - 1; i++) {

  document.write('<g transform="translate(200,200)scale('+(400/range)+', '+(-400/range)+')">');

  document.write('<line x1='+Ux[i]+' y1='+Uy[i]+' x2='+Ux[i+1]+' y2='+Uy[i+1]+' stroke="black" stroke-width='+range/400*1+' />');

  document.write('</g>');

};

グラフを描く部分はこれまでのコードとほとんど同じものです。今回は配列の大きさにもとづいて辺の数だけ直線をひいています。

今回はベクトルを用いて求めたい点の座標を計算してみました。コンピューターで図形を描くときには必ず座標を必要とするので，数IIBのベクトルが役に立つことが分かると思います。