【JavaScript】円のグラフを描く―中心が原点でない場合
以前に原点を円の中心とするグラフを描いてみましたが,もう少しグレードアップして中心が原点ではない円のグラフを描いてみましょう。
<!DOCTYPE html><html><body><script>
//関数f(x)を定義する
let f = e => {
let n = 4-Math.pow((e-1),2); // 4-(x-1)^2をnに代入
if (Math.abs(n) < 0.05) n = 0; //nの絶対値が0に近いとき,n=0とする
let yPlus = Math.sqrt(n)+1;
let yMinus = -Math.sqrt(n)+1;
return [yPlus, yMinus];
};
const range = 8; // x軸両端の幅
let x = -range/2; //始点のx座標
//軸線を描く
document.write('<svg width=400 height=400><line x1=0 y1=200 x2=400 y2=200 stroke="black"/><line x1=200 y1=0 x2=200 y2=400 stroke="black"/>');
//関数のグラフを描く
for(let i=0; i < 400; i++) { //処理を4000回繰り返し
//始点と終点の座標をもとに直線を引く
//直線の始点の上側のy座標をyPlus1,下側をyMinus1とする
let [yPlus1, yMinus1] = f(x);
//直線の終点の上側のy座標をyPlus2,下側をyMinus2とする
let [yPlus2, yMinus2] = f(x+range/400);
if ((isNaN(yPlus1) == false) && (isNaN(yPlus2) == false)) {
//円の上側を描画
document.write('<g transform="translate(200,200)scale('+(400/range)+', '+(-400/range)+')"><line x1='+x+' y1='+yPlus1+' x2='+(x+range/400)+' y2='+yPlus2+' stroke="blue" stroke-width='+range/400*2+' /></g>');
//円の下側を描画
document.write('<g transform="translate(200,200)scale('+(400/range)+', '+(-400/range)+')"><line x1='+x+' y1='+yMinus1+' x2='+(x+range/400)+' y2='+yMinus2+' stroke="blue" stroke-width='+range/400*2+' /></g>');
};
x += range/400; // xの値を次の点の座標にする
};
//最後にタグを閉じる
document.write('</svg>');
</script></body></html>
関数を定義する
//関数f(x)を定義する
let f = e => {
let n = 4-Math.pow((e-1),2); // 4-(x-1)^2をnに代入
if (Math.abs(n) < 0.05) n = 0; //nの絶対値が0に近いとき,n=0とする
let yPlus = Math.sqrt(n)+1;
let yMinus = -Math.sqrt(n)+1;
return [yPlus, yMinus];
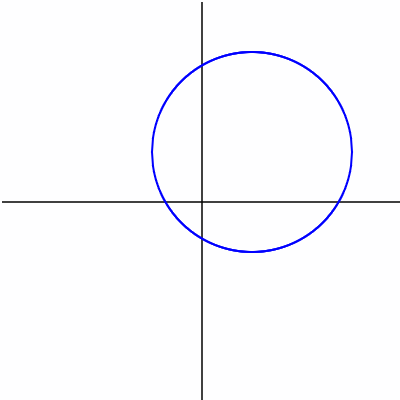
};今回描く円の方程式は $(x-1)^2+(y-1)^2=2^2$ です。これは中心 $(1,1)$,半径 $2$ の円を表します。式を変形すると
$(y-1)^2=4-(x-1)^2$
$y-1=\pm\sqrt{4-(x-1)^2}$
$y=\pm\sqrt{4-(x-1)^2}+1$
となります。一つの $x$ の値に対して $y$ の値が 2 つ出てきます。それぞれ円の上半分と下半分の $y$ 座標を意味します。
今回は Math.pow() を使ってみます。これは累乗を求める関数で,例えば Math.pow(2, 3) は $2^3=8$ ということです。これを使ってルートの中の $4-(x-1)^2$ の値を n に代入します。
次の行では if (Math.abs(n) < 0.05) n = 0; となっています。Math.abs() は絶対値を求める関数で,ここでは n の絶対値を表します。文の意味は「n の絶対値が $0.05$ より小さければ n =0 とする。」ということです。
このような処理を行っているのは,次の文で Math.sqrt() を使って平方根を求める際の誤作動を修正するためです。4-Math.pow((e-1),2) という計算は実は微小な誤差を含んでいて,本来 $0$ になるべきところが $0$ に近い微小な負の小数になることがあります。Math.sqrt() は負の値を代入することができないので,このままだと円の左右の端の辺りが描かれないという問題が発生します。そこで,$-0.05$ < $n$ < $0.05$ の範囲にある値を強制的に $0$ とすることで修正しています。
上で述べた通り解は 2 つ出てくるので,ルートの前に+がついている解を yPlus,-がついている解を yMinus として代入します。
最後の return [yPlus, yMinus]; で結果を返します。このように書くことで複数の解を返すことができます。
2 つの解を代入する
//直線の始点の上側のy座標をyPlus1,下側をyMinus1とする
let [yPlus1, yMinus1] = f(x);
//直線の終点の上側のy座標をyPlus2,下側をyMinus2とする
let [yPlus2, yMinus2] = f(x+range/400);あとは,定義した関数の結果をもとにグラフを描いていきます。グラフを描く部分はこれまでのものとほとんど同じなのですが,今回は解をいったん変数に代入してから描いています。関数 f(x) は解を二つ持ちますが,上のように書くことでそれぞれの解を yPlus1 と yMinus1 に代入することができます。あとはこれらの座標をもとに円の上側と下側を別々に描くことで,円の出来上がりです。
if ((isNaN(yPlus1) == false) && (isNaN(yPlus2) == false)) {
//円の上側を描画
document.write('<g transform="translate(200,200)scale('+(400/range)+', '+(-400/range)+')"><line x1='+x+' y1='+yPlus1+' x2='+(x+range/400)+' y2='+yPlus2+' stroke="blue" stroke-width='+range/400*2+' /></g>');
//円の下側を描画
document.write('<g transform="translate(200,200)scale('+(400/range)+', '+(-400/range)+')"><line x1='+x+' y1='+yMinus1+' x2='+(x+range/400)+' y2='+yMinus2+' stroke="blue" stroke-width='+range/400*2+' /></g>');
};グラフを描画する部分も少し工夫しています。isNaN() は変数の値が数値であるでないかどうかを判定する関数です。ここでは isNaN(yPlus1) として 変数 yPlus1 が数値でないかどうかを判定しています。つまり isNaN(yPlus1) == false は,「yPlus1が数値であるならば」という意味になります。
このような判定を行っているのは,定義した関数ではルートの中に負の数が入ると NaN(数字ではない) という特殊な形を返してくるので,その場合にはグラフを描画しないようにしているのです。
このあたりは数学で円の方程式を習うときにあまり触れられない部分ですが,$(x-1)^2+(y-1)^2=2^2$ という円の方程式に $x=-5$ などの円の外側の座標を代入すると $y$ は虚数になります。虚数はグラフ上の点として描くことができないので,存在しないものとして描かないのです。
今回は,関数 $y=f(x)$ が複数の解を持つときの解の扱い方を学びました。これを使えばさまざまな二字曲線のグラフを描くことができるようになります。
SNSでシェア