【JavaScript】ax+b型の漸近線を描く
前回は y 軸に平行な漸近線を描きましたが,今回は ax+b 型の漸近線を描いてみます。
<!DOCTYPE html>
<html>
<body>
<script>
//関数f(x)を定義する
let f = x => x ** 2 / (x - 1);
let fdRight = x => {
let yd = (f(x + h) - f(x)) / h;
//ydが計算不能なときは代わりに 0.0001を返す
if (isNaN(yd) == true) return 0.0001;
return yd;
}
let fdLeft = x => {
let yd = (f(x) - f(x - h)) / h;
if (isNaN(yd) == true) return 0.0001;
return yd;
}
const Range = 18; // x軸両端の幅
const range = Range / 400;
let x = -Range / 2; //始点のx座標
const h = range; // 1/∞の代わりに0に近い小さな値を設定する
//軸線を描く
document.write('<svg width=400 height=400><line x1=0 y1=200 x2=400 y2=200 stroke="black"/><line x1=200 y1=0 x2=200 y2=400 stroke="black"/><g transform="translate(200,200)scale(' + (1 / range) + ', ' + (-1 / range) + ')">');
//ax+b型漸近線をひく
let m = 1000; //∞の代わりにある大きな値を設定する
let n = 1001;
//f(m)とf(n)の微分係数がほとんど同じであればそれを漸近線の傾きであると判定
if (Math.abs(fdRight(m) - fdRight(n)) < 0.001) {
//漸近線をg(x)として定義
let g = x => fdRight(m) * (x - m) + f(m);
//ax+b漸近線の描画
document.write('<line x1=' + (-Range / 2) + ' y1=' + g(-Range / 2) + ' x2=' + (Range / 2) + ' y2=' + g(Range / 2) + ' stroke="green" stroke-width="' + range + '" stroke-dasharray=0.1 />');
}
//f(-m)とf(-n)の微分係数がほとんど同じであればそれを漸近線の傾きであると判定
if (Math.abs(fdRight(-m) - fdRight(-n)) < 0.001) {
//漸近線をg(x)として定義
let g = x => fdRight(-m) * (x - m) + f(-m);
//ax+b漸近線の描画
document.write('<line x1=' + (-Range / 2) + ' y1=' + g(-Range / 2) + ' x2=' + (Range / 2) + ' y2=' + g(Range / 2) + ' stroke="green" stroke-width="' + range + '" stroke-dasharray=0.1 />');
}
//関数のグラフを描く
for (let i = 0; i < 400; i++) { //処理を400回繰り返し
//y軸平行漸近線の処理
if (fdLeft(x) * fdRight(x) < -1) {
//y軸に平行な漸近線をひく
if (fdLeft(x + range) * fdRight(x + range) > 0) {
document.write('<line x1=' + x + ' y1=' + Range / 2 + ' x2=' + x + ' y2=' + (-Range / 2) + ' stroke="green" stroke-width="' + range +
'" stroke-dasharray=0.1 />');
}
} else {
//始点と終点の座標をもとに直線をひく
document.write('<line x1=' + x + ' y1=' + f(x) + ' x2=' + (x + range) + ' y2=' + f(x + range) + ' stroke="blue" stroke-width="' + range * 2 + '" />');
}
x += range; // xの値を次の点の座標にする
}
//最後にタグを閉じる
document.write('</g></svg>');
</script>
</body>
</html>
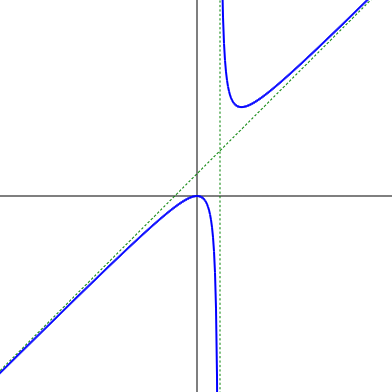
関数のグラフ
//関数f(x)を定義する
let f = x => x ** 2 / (x - 1);今回描いているグラフは $f(x)=\cfrac{x^2}{x-1}$ です。また,前回のコードを使って $x=1$ のところに y 軸に平行な漸近線がひかれています。
ax+b型漸近線の定義
$ax+b$ 型の漸近線を考えるとき,数IIIの微分で習った定義は
$\displaystyle\lim_{x\rightarrow\infty}\{f(x)-(ax+b)\}=0$ または $\displaystyle\lim_{x\rightarrow-\infty}\{f(x)-(ax+b)\}=0$ であるとき,直線 $y=ax+b$ は漸近線である。
というものでした。ようするに,関数のグラフをどんどん伸ばしていったときに,グラフがある直線に限りなく近づいていく,ということです。
ただし,この方法でははじめに $ax+b$ を決める必要があります。数学の問題として解くときは式変形から直線の式を見抜いていくのですが,コンピューターにそれをさせるのはタイヘンそうです(高校生だって苦労するところですよね)。したがって,代わりの方法を考えます。
ax+b型漸近線の判定
//ax+b型漸近線をひく
let m = 1000; //∞の代わりにある大きな値を設定する
let n = 1001;
//f(m)とf(n)の微分係数がほとんど同じであればそれを漸近線の傾きであると判定
if (Math.abs(fdRight(m) - fdRight(n)) < 0.001) {関数 $f(x)$ が $ax+b$ 型の漸近線を持つとき,$x$ の値をどんどん大きくしていくと漸近線に限りなく近づいていきます。これは言い換えれば $f(x)$ の接線の傾きが漸近線の傾きとほとんど等しくなるということです。
そこで∞の代わりにある大きな値を二つ用意します。ここでは $m=1000$,$n=1001$ としています。そして $x$ の値が $m$ と $n$ のときの接線の傾きを求め,それぞれの傾きがほとんど同じであれば漸近線が存在するということにします。判定のところを数学の式として書くと
$|f'(m)-f'(n)| < 0.001$ ならば,漸近線が存在する
ということです。$f(x)$ において $x=m$ と $x=n$ のときの接線の傾きがほとんど同じであれば $|f'(m)-f'(n)|$ の値は $0$ に近い小さな値をとるはずです。
これで漸近線の判定ができたので,実際に漸近線をひいてみましょう。
漸近線の描画
//ax+b型漸近線をひく
let m = 1000; //∞の代わりにある大きな値を設定する
let n = 1001;
//f(m)とf(n)の微分係数がほとんど同じであればそれを漸近線の傾きであると判定
if (Math.abs(fdRight(m) - fdRight(n)) < 0.001) {
//漸近線をg(x)として定義
let g = x => fdRight(m) * (x - m) + f(m);
//ax+b漸近線の描画
document.write('<line x1=' + (-Range / 2) + ' y1=' + g(-Range / 2) + ' x2=' + (Range / 2) + ' y2=' + g(Range / 2) + ' stroke="green" stroke-width="' + range + '" stroke-dasharray=0.1 />');
}
//f(-m)とf(-n)の微分係数がほとんど同じであればそれを漸近線の傾きであると判定
if (Math.abs(fdRight(-m) - fdRight(-n)) < 0.001) {
//漸近線をg(x)として定義
let g = x => fdRight(-m) * (x - m) + f(-m);
//ax+b漸近線の描画
document.write('<line x1=' + (-Range / 2) + ' y1=' + g(-Range / 2) + ' x2=' + (Range / 2) + ' y2=' + g(Range / 2) + ' stroke="green" stroke-width="' + range + '" stroke-dasharray=0.1 />');
}漸近線の描画は $x\rightarrow+\infty$ のときと $x\rightarrow-\infty$ のときに分けて行います。
漸近線であると判定したら,$f(m)$ における接線を漸近線として代用します。
接線を $g(x)$ とすると $x=m$ における接線の式は $g(x)=f'(m)(x-m)+f(m)$ となります。あとはこれに基づいて描画範囲の左端から右端まで点線をひいています。
あとは,$m$,$n$ を $-m$,$-n$ として $x\rightarrow-\infty$ のときの漸近線をひきます。
上のグラフでは $-\infty$ の側の漸近線はありません。
そこで,$f(x)=\cfrac{e^x}{x}+1$ のグラフで確かめてみましょう。関数 $f(x) の定義の部分を
let f = x => 2.7**x/x+1;と書き換えます。$e$ は $2.7$ で代用します。
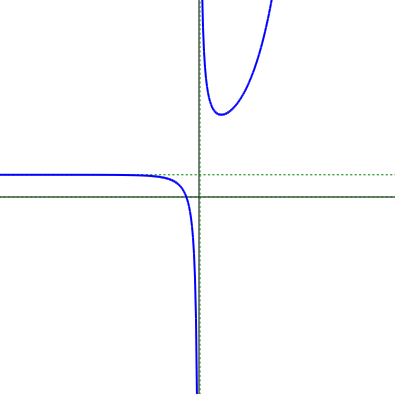
$y=1$ の漸近線がひかれました。画面上では $x$ 軸に平行に見えますが,実際には $0$ に近いごく小さな傾きを持つ $y=ax+b$ の直線です。
SNSでシェア