【スマホで読む・わかりやすい】共通テスト数学IA2022追試【解説・正解・問題】
第5問 正解
ア,イ 0, 1 (解答の順序は問わない)
ウ,エ 2, 5 オ,カ 1, 2
キ,ク 1, 4 ケ,コ 6, 5
サ,シ,ス,セ 4, 5, 9, 5
ソ,タチ,ツテ 2, 15, 15
ト,ナ,ニヌ 4, 6, 15
(1)
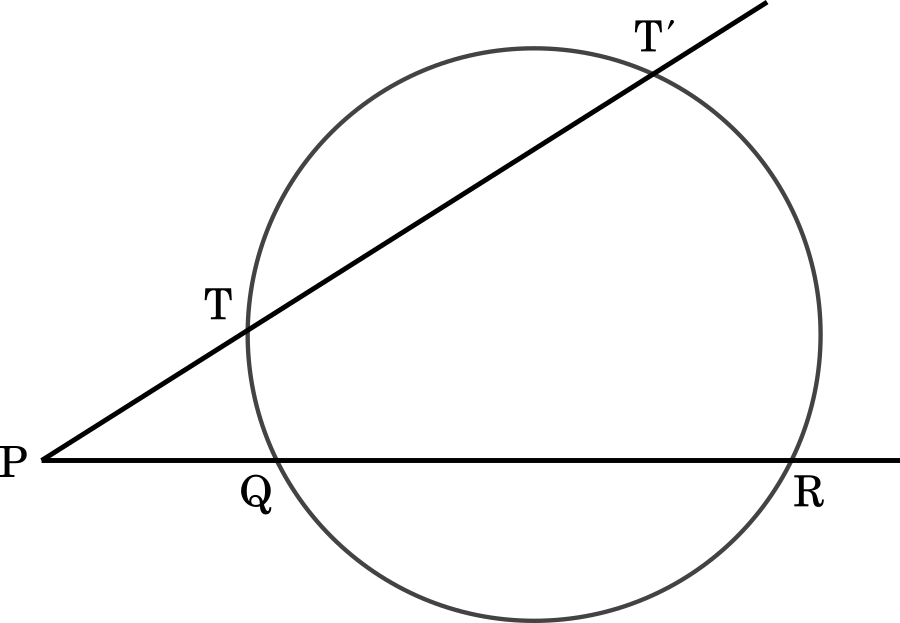
方べきの定理より
PT・PT’ = PQ・PR
・・・ア,イ
(2)

△ABC において,角の二等分線の性質より
$\begin{aligned}\text{AD}:\text{CD}&=\text{AB}:\text{BC}\\&=\cfrac{1}{2}:\cfrac{3}{4}\\&=2:3\end{aligned}$
したがって
$\text{AD}=1\times\cfrac{2}{5}=\cfrac{2}{5}$
・・・ウ,エ
次に,△ABE において,角の二等分線の性質より
$\begin{aligned}\text{AF}:\text{EF}&=\text{AB}:\text{BE}\\&=\cfrac{1}{2}:\cfrac{3}{4}\\&=2:3\end{aligned}$
メネラウスの定理より
$\cfrac{\text{EB}}{\text{BC}}\times\cfrac{\text{CG}}{\text{GA}}\times\cfrac{\text{AF}}{\text{FE}}=1$
$\cfrac{1}{1}\times\cfrac{\text{CG}}{\text{GA}}\times\cfrac{2}{3}=1$
$\cfrac{\text{CG}}{\text{GA}}=\cfrac{3}{2}$
よって
$\cfrac{\text{AC}}{\text{AG}}=\cfrac{1}{2}$
・・・オ,カ
次に,
$\cfrac{\textsf{△ABFの面積}}{\textsf{△AFGの面積}}$ を求める。
AC : AG = 1 : 2 より
△ABG : △ABC = 1 : 2
△ABG = 2 × △ABC
BC = BE より,△ABC = △ABE となるので
△ABG = 2 × △ABE ・・・①
また
△ABG = △ABF + △AFG
①を代入して
2 × △ABE = △ABF + △AFG ・・・②
ここで,AF : EF = 2 : 3 より
△ABF = $\cfrac{2}{5}$ × △ABE
△ABE = $\cfrac{5}{2}$ × △ABF
②に代入して
2 × $\cfrac{5}{2}$ × △ABF = △ABF + △AFG
5 × △ABF = △ABF + △AFG
4 × △ABF = △AFG
したがって
$\cfrac{\triangle\text{ABF}}{\triangle\text{AFG}}=\cfrac{1}{4}$
・・・キ,ク
線分 DG の中点を H とする。

$\cfrac{\text{AC}}{\text{AG}}=\cfrac{1}{2}$ より
AG = 2
DG = AG + AD より
$=2+\cfrac{2}{5}$
$=\cfrac{12}{5}$
DG の中点が H なので
$\text{DH}=\cfrac{1}{2}\times\text{DG}$
$=\cfrac{1}{2}\times\cfrac{12}{5}$
$=\cfrac{6}{5}$
よって
CH = CD + DH
$=\cfrac{3}{5}+\cfrac{6}{5}=\cfrac{9}{5}$
・・・ス,セ
AH = DH – AD
$=\cfrac{6}{5}-\cfrac{2}{5}$
$=\cfrac{4}{5}$
・・・サ,シ
△ABC と △BCH において
余弦定理より
$\text{AB}^2=\text{BC}^2+\text{AC}^2-2\cdot\text{BC}\cdot\text{AC}\cdot\cos\angle\text{ACB}$
$\Big(\cfrac{1}{2}\Big)^2=\Big(\cfrac{3}{4}\Big)^2+1-2\cdot\cfrac{3}{4}\cdot1\cdot\cos\angle\text{ACB}$
$\cfrac{1}{4}=\cfrac{9}{16}+1-\cfrac{3}{2}\cos\angle\text{ACB}$
両辺を 16 倍して
$4=9+16-24\cos\angle\text{ACB}$
$24\cos\angle\text{ACB}=9+16-4$
$=21$
$\cos\angle\text{ACB}=\cfrac{21}{24}=\cfrac{7}{8}$
また
$\text{BH}^2=\text{BC}^2+\text{CH}^2-2\cdot\text{BH}\cdot\text{CH}\cdot\cos\angle\text{BCH}$
$\cos\angle\text{ACB}=\cos\angle\text{BCH}$ なので
$\text{BH}^2=\Big(\cfrac{3}{4}\Big)^2+\Big(\cfrac{9}{5}\Big)^2-2\cdot\cfrac{3}{4}\cdot\cfrac{9}{5}\cdot\cfrac{7}{8}$
$=\cfrac{9}{16}+\cfrac{81}{25}-\cfrac{189}{80}$
$=\cfrac{225+1296-945}{400}$
$=\cfrac{576}{400}$
$=\cfrac{144}{100}$
よって
$\text{BH}=\cfrac{12}{10}=\cfrac{6}{5}$
・・・ケ,コ
△ABC の外心を O とすると,正弦定理より
$\cfrac{\text{AB}}{\sin\angle\text{ACB}}=2R$
$2R=\cfrac{\cfrac{1}{2}}{\space\cfrac{\sqrt{15}}{8}\space}$
$2R=\cfrac{\cfrac{1}{2}\times8}{\space\cfrac{\sqrt{15}}{8}\times8\space}$
$=\cfrac{4}{\sqrt{15}}$
$R=\cfrac{2}{\sqrt{15}}$
$=\cfrac{2\sqrt{15}}{15}$
・・・ソ,タチ,ツテ
また
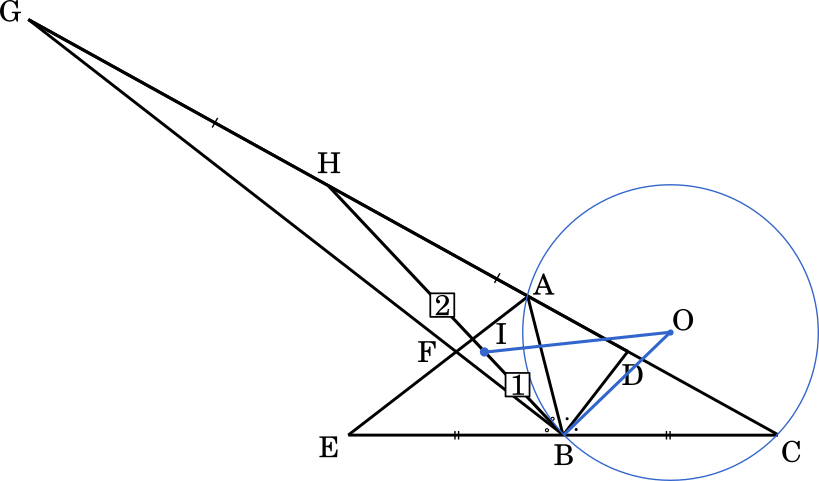
$\text{AH}=\cfrac{4}{5},\text{BH}=\cfrac{6}{5},\text{CH}=\cfrac{9}{5}$ より
$\text{AH}\cdot\text{CH}=\cfrac{4}{9}\cdot\cfrac{4}{5}=\cfrac{36}{25}$
$\text{BH}^2=\Big(\cfrac{6}{5}\Big)^2=\cfrac{36}{25}$
よって
$\text{AH}\cdot\text{CH}=\text{BH}^2$
が成り立つ。
つまり,方べきの定理の逆が成り立つので,$\angle\text{HBO}$ は直角であることが分かる。
BI : IH = 1 : 2 より
$\text{BI}=\cfrac{1}{3}\times\text{BH}$
$=\cfrac{1}{3}\times\cfrac{6}{5}$
$=\cfrac{2}{5}$
△BIO において,三平方の定理より
$\text{BI}^2+\text{BO}^2=\text{IO}^2$
$\text{IO}^2=\Big(\cfrac{2}{5}\Big)^2+\Big(\cfrac{2\sqrt{15}}{15}\Big)^2$
$=\cfrac{4}{25}+\cfrac{60}{225}$
$=\cfrac{36+60}{225}$
$=\cfrac{96}{225}$
したがって
$\text{IO}=\cfrac{4\sqrt{6}}{15}$
・・・ト,ナ,ニヌ
問題文
第3問~第5問は,いずれか2問を選択し,解答しなさい。
第5問
(1) 円と直線に関する次の定理を考える。
定理
3 点 P,Q,R は一直線上にこの順に並んでいるとし,点 T はこ の直線上にないものとする。このとき,PQ・PR = PT$^2$ が成り立つならば,直線 PT は 点 Q,R,T を通る円に接する。
この定理が成り立つことは,次のように説明できる。
直線 PT は 3 点 Q,R,T を通る円 O に接しないとする。このとき,直線 PT は円 O と異なる 2 点で交わる。直線 PT と円 O との交点で点 T とは異なる 点を T′とすると
$\text{PT}\cdot\text{PT}’=\boxed{\boxed{\textsf{ア}}}\cdot\boxed{\boxed{\textsf{イ}}}$
が成り立つ。点 T と点 T′ が異なることにより,PT・PT′ の値と PT$^2$ の値は異なる。したがって,PQ・PR = PT$^2$ に矛盾するので,背理法により,直線 PT は 点 Q,R,T を通る円に接するといえる。
$\boxed{\boxed{\text{ア}}}$,$\boxed{\boxed{\text{イ}}}$ の解答群(解答の順序は問わない。)
$\text{\textcircled 0}$ PQ ① PR ② QR ③ QT ④ RT
(2) △ABC において,AB = $\cfrac{1}{2}$ ,BC = $\cfrac{3}{4}$,AC = 1 とする。このとき,∠ABC の二等分線と辺 AC との交点を D とすると,AD = $\cfrac{\enspace\boxed{\textsf{ウ}}\enspace}{\boxed{\textsf{エ}}}$ である。直線 BC 上に,点 C とは異なり,BC = BE となる点 E をとる。∠ABE の二等分線と線分 AE との交点を F とし,直線 AC との交 点を G とすると
$\cfrac{\text{AC}}{\text{AG}}=\cfrac{\enspace\boxed{\textsf{オ}}\enspace}{\boxed{\textsf{カ}}}$,$\cfrac{\text{△ABF}\textsf{の面積}}{\text{△AFG}\textsf{の面積}} = \cfrac{\enspace\boxed{\textsf{キ}}\enspace}{\boxed{\textsf{ク}}}$
である。
線分 DG の中点を H とすると,BH = $\cfrac{\enspace\boxed{\textsf{ケ}}\enspace}{\boxed{\textsf{コ}}}$
である。また
AH = $\cfrac{\enspace\boxed{\textsf{サ}}\enspace}{\boxed{\textsf{シ}}}$,CH = $\cfrac{\enspace\boxed{\textsf{ス}}\enspace}{\boxed{\textsf{セ}}}$
である。
△ABC の外心を O とする。 △ABC の外接円 O の半径が
$\cfrac{\boxed{\textsf{ソ}}\sqrt{\boxed{\textsf{タチ}}}}{\boxed{\textsf{ツテ}}}$ であることから,線分 BH を 1 : 2 に内分する点を I とすると
IO = $\cfrac{\boxed{\textsf{ト}}\sqrt{\boxed{\textsf{ナ}}}}{\boxed{\textsf{ニヌ}}}$
であることがわかる。
SNSでシェア