【スマホで読む・わかりやすい】共通テスト数学IA2022追試【解説・正解・問題】
第2問 正解
ア 4 イ ウ,エ 25, 2
オカ 12 キク 10
ケコ,サ 15, 2
シス,セソ,タチツ -2, 30, 100
テ 6 ト 1 ナ 1
ニ,ヌ 1,5 (解答の順序は問わない)
ネノ 57 ハ 3 ヒ 2
フ 2 ヘ,ホ 0, 2
〔1〕
(1)
AP = $x$ とする。
・$a=6$ のとき
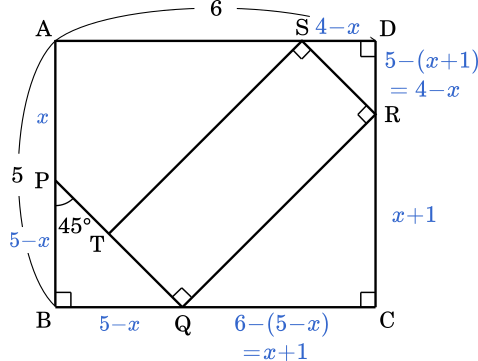
$\ell$ が頂点 C, D 以外の点で辺 CD と交わるとき
$x+1<5$
$x<4$
が成り立つ。
また,点 P は辺 AB 上の点なので,$x$ は 0 以上である。したがって
$0\leqq\text{AP}<4$
・・・ア
△QCR は辺の比が $1:1:\sqrt{2}$ の直角二等辺三角形なので
QR = $\sqrt{2}(x+1)$
RS = $\sqrt{2}(4-x)$
四角形 QRST の面積は
$S=\sqrt{2}(x+1)\times\sqrt{2}(4-x)$
$=2(4x-x^2+4-x)$
式を平方完成して最大値を求めると
$=2(-x^2+3x)+8$
$=-2(x^2-3x)+8$
$=-2\Big(x-\cfrac{3}{2}\Big)^2+\cfrac{9}{2}+8$
$=-2\Big(x-\cfrac{3}{2}\Big)^2+\cfrac{25}{2}$
$x=\cfrac{3}{2}$ のとき,最大値 $\cfrac{25}{2}$
したがって,面積の最大値は
$\cfrac{25}{2}$
・・・イウ,エ
・$a=8$ のとき
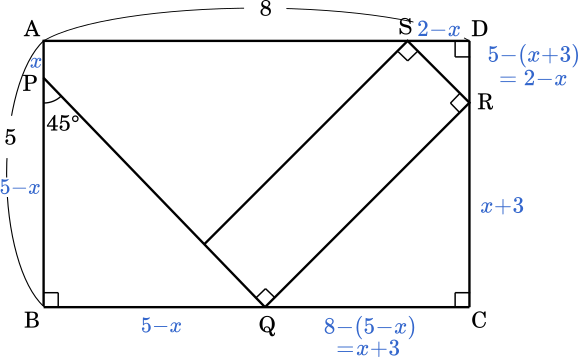
$S=\sqrt{2}(x+3)\times\sqrt{2}(2-x)$
$=2(x+3)(2-x)$
$=2(2x-x^2+6-3x)$
$=2(-x^2-x)+12$
$=-2(x^2+x)+12$
$=-2\Big(x+\cfrac{1}{2}\Big)^2+\cfrac{1}{2}+12$
$=-2\Big(x+\cfrac{1}{2}\Big)^2+\cfrac{25}{2}$
ここで AP の範囲を考えると
$x+3<5$
$x<2$
よって $0\leqq\text{AP}<2$

$x=0$ で最大となるので,これを代入すると
$S=-2(x^2+x)+12$
$=12$
・・・オカ
(2)
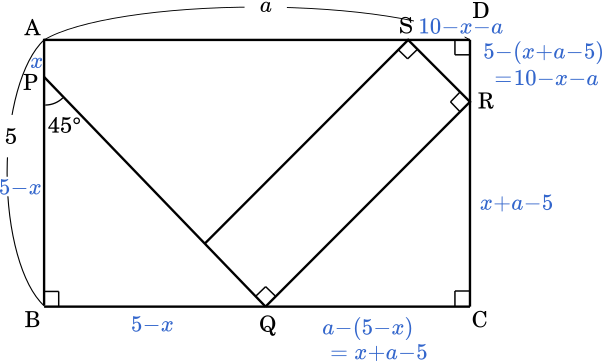
$x+a-5<5$
$x<10-a$
したがって
$0\leqq\text{AP}<10-a$ ・・・①
・・・キク
次に,四角形の面積が最大となるのはどのような場合かを考える。
$a$ の値に関係なく CR,DR の長さの和は 5 であることから,QR と SR の和も一定である。
四角形の縦と横の長さの和が一定の場合,その四角形が正方形のときに面積が最大となり,その値は $a=6$ のときに求めた $\cfrac{25}{2}$ である。
$a=6$,$a=8$ のときを振り返ると,面積のグラフの頂点が①の範囲にあるときに最大値が $\cfrac{25}{2}$ となることが分かる。
面積を求めると
$S=\sqrt{2}(x+a-5)\times\sqrt{2}(10-x-a)$
$=2(10x-x^2-ax+10a-ax-a^2-50+5x+5a)$
$=2\{-x^2+(15-2a)x+a^2+15a-50\}$
$=-2\Big\{x^2-(15-2a)x\Big\}+2a^2+30a-100$
$=-2\Big(x-\cfrac{15-2a}{2}\Big)^2+\cfrac{(15-2a)^2}{2}+2a^2+30a-100$
よって $x=\cfrac{15-2a}{2}$ のとき最大となる。
①の不等式の左側より
$0\leqq \cfrac{15-2a}{2}$
$0\leqq15-2a$
$2a\leqq15$
$a\leqq\cfrac{15}{2}$
不等式の右側からは $a$ の範囲を求めることはできない。
したがって
$5<a\leqq\cfrac{15}{2}$
・・・ケコ,サ
$a$ が $\cfrac{15}{2}<a<10$ を満たすとき
$a=8$ のときを振り返ると,面積のグラフは頂点の $x$ 座標が負の数になる。よって,面積は AP = 0 で最大値をとる。
$S=\sqrt{2}(x+a-5)\times\sqrt{2}(10-x-a)$
に $x=0$ を代入すると
$=\sqrt{2}(a-5)\times\sqrt{2}(10-a)$
$=2(10a-a^2-50+5a)$
$=2(-a^2+15a-50)$
$-2a^2+30a-100$
・・・シス,セソ,タチツ
〔2〕
(1)
速度についての比の値は
$9.60\div82.0=0.117\cdots$
小数第 3 位を四捨五入して 0.12
・・・テ
相関係数
$r=\cfrac{s_{xy}}{s_x s_y}$
$s_{xy}$: $x$ と$y$ の共分散
$s_x$: $x$ の標準偏差
$s_y$: $y$ の標準偏差
交通量と速度の相関係数は
$r=\cfrac{-63600}{10200\times9.60}$
$=-0.649\cdots$
小数第 3 位を四捨五入すると $-0.65$
・・・ト
次に,2015年の交通量のヒストグラムについて考える。
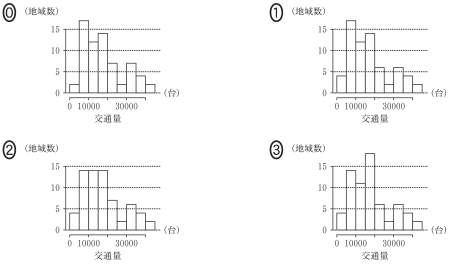
図 1 より交通量が 5000 未満の個数を数えると 4 個あるので,選択肢は①,②,③のいずれかである。
さらに交通量が 5000 以上 10000 未満の個数を数えると 17 個あるので,①が正しい。
・・・ナ
また,表 1 および図 1 から読み取れることとして,正しいものを考えると
⓪ 75 以上の地域が存在するので不適。
① 正しい。
② 速度の平均値は 82.0 で,交通量の平均値は 17300 である。速度が平均値以上の地域で,交通量が平均値未満の地域が存在するので不適。
③ 速度が平均値未満で,交通量が平均値以上の地域が存在するので不適。
④ 交通量が 27500 以上の地域は,13 個あるので不適。
⑤ 正しい。
よって,①と⑤が正しい。
・・・ニ,ヌ
(2)
図 2 を見ると,傾きが 1 である直線より上にある地域が A 群で,下にある地域が B 群である。全 67 地域で,B 群の地域数が 10 であることから,A 群の個数は $67-10=57$ である。
・・・ネノ
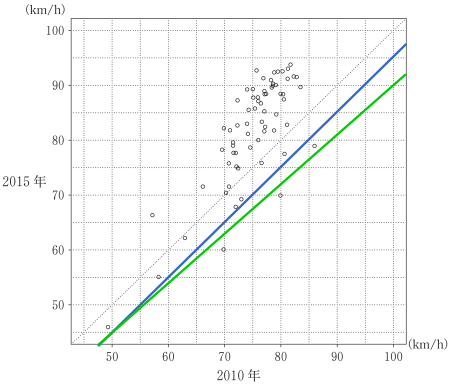
また,B 群において,2010 年より 2015 年の速度が,5 km/h 以上遅くなった地域数は,上の図の青色の線より下にある地域なので,地域数は 3 である。
・・・ハ
10 %以上遅くなった地域数は緑色の線より下の地域なので,地域数は 2 である。
・・・ヒ
緑色の直線は,2010年 が 50 のとき 2015年は 50 × 0.9 = 45,2010年が 100 のとき 2015 年は 100 × 0.9 = 90 としてそれぞれ点をとり,それらの 2 点を結ぶ直線を引けば良い。
次に,A 群と B 群の 2015 年の速度について考える。このとき 2015 年の速度であるから,それぞれのデータを図の縦方向で比べることに注意する。
(I) A 群の範囲はおよそ 66 以上 94 未満であり,B 群の範囲はおよそ 46 以上 79 未満であるから,正しい。
(II) B 群の速度の第 3 四分位数は,データの個数が 10 個であることから,値が最も大きいものから数えて 3 番目のデータであり,その値はおよそ 76 である。A 群の速度の第 1 四分位数は 81.2 なので,誤り。
$\circ\circ\underbrace{\circ}_{\textsf{第1四分位数}}\circ\circ|\circ\circ\underbrace{\circ}_{\textsf{第3四分位数}}\circ\circ$
(III) A 群の速度の四分位範囲は $89.7-81.2=8.5$ である。また,B 群の第1四分位数は,値が最も小さいものから数えて 3 番目のデータであり,その値はおよそ 63 であるから,その四分位範囲は $76-63=13$ である。よって,正しい。
従って(I), (II), (III)の正誤の組合せとして正しいものは②である。
・・・フ
(3)
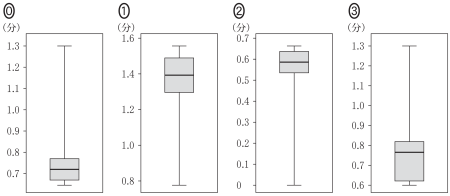
図 1 より速度の最大値はおよそ 93 である。
$\cfrac{1}{93}\times60=0.64\cdots$
このとき,速度と 1 kmあたりの走行時間は反比例の関係にあるので,速度の最大値は 1 kmあたりの走行時間の最小値に変換されることに注意する。
したがって,箱ひげ図は⓪が正しい。
・・・ヘ
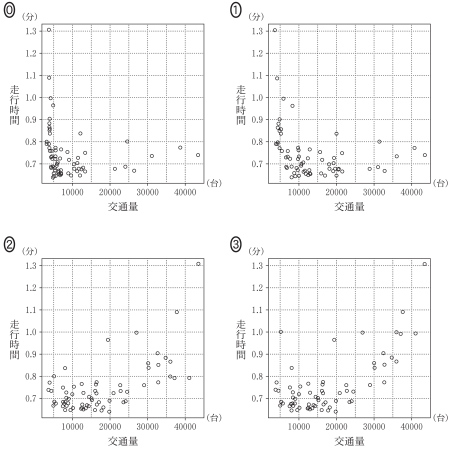
これを踏まえると,2015 年の交通量と速度は負の相関があるので,2015 年の交通量と 1km あたりの走行時間は正の相関になる。よって,選択肢は②また③に絞ることができる。
次に,最も大きいものから 2 番目のデータに着目すると良い。速度はおよそ 76 なので,
$\cfrac{1}{76}\times60=0.78\cdots$
となる。したがって,②が正しい。
・・・ホ
問題文
〔1〕 $a$ を 5 < $a$ < 10 を満たす実数とする。長方形 ABCD を考え,AB = CD = 5,BC = DA = $a$ とする。
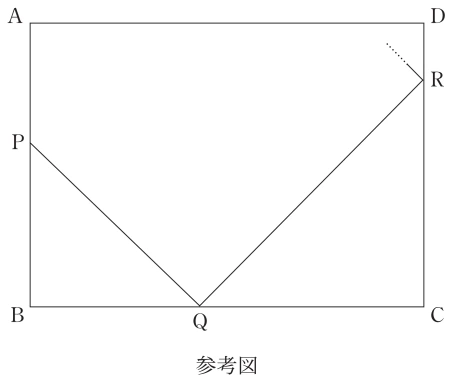
次のようにして,長方形 ABCD の辺上に 点 P,Q,R,S をとり,内部 に点 T をとることを考える。
辺 AB 上に点 B と異なる点 P をとる。辺 BC 上に点 Q を ∠BPQ が 45° になるようにとる。Q を通り,直線 PQ と垂直に交わる直線を $\ell$ とする。$\ell$ が 頂点 C,D 以外の点で辺 CD と交わるとき,$\ell$ と辺 CD の交点を R とする。
点 R を通り $\ell$ と垂直に交わる直線を $m$ とする。$m$ と辺 AD との交点を S とする。点 S を通り $m$ と垂直に交わる直線を $n$ とする。$n$ と直線 PQ との 交点を T とする。
(1) $a$ = 6 のとき,$\ell$ が頂点 C,D 以外の点で辺 CD と交わるときの AP の 値の範囲は 0 ≦ AP < $\boxed{\textsf{ア}}$ である。このとき,四角形 QRST の面積の最大値は $\cfrac{\boxed{\textsf{イウ}}}{\boxed{\textsf{エ}}}$ である。
$a$ = 8 のとき,四角形 QRST の面積の最大値は $\boxed{\textsf{オカ}}$ である。
(2) 5 < $a$ < 10 とする。$\ell$ が頂点 C,D 以外の点で辺 CD と交わるときの AP の値の範囲は
0 ≦ AP < $\boxed{\textsf{キク}}$ - $a$ ・・・①
である。
点 P が ① を満たす範囲を動くとする。四角形 QRST の面積の最大値が $\cfrac{\boxed{\text{イウ}}}{\boxed{\text{エ}}}$ となるときの $a$ の値の範囲は
5 < $a$ ≦ $\cfrac{\boxed{\textsf{ケコ}}}{\boxed{\textsf{サ}}}$
である。
a が $\cfrac{\boxed{\text{ケコ}}}{\boxed{\text{サ}}}$ < $a$ < 10 を満たすとき,P が ① を満たす範囲を動いたときの四角形 QRST の面積の最大値は
$\boxed{\textsf{シス}}\space a^2+\boxed{\textsf{セソ}}\space a-\boxed{\textsf{タチツ}}$
である。
〔2〕国土交通省では「全国道路・街路交通情勢調査」を行い,地域ごとのデータを公開している。以下では,2010 年と 2015 年に 67 地域で調査された高速道路の交通量と速度を使用する。交通量としては,それぞれの地域におい て,ある 1 日にある区間を走行した自動車の台数(以下,交通量という。単位は台)を用いる。また,速度としては,それぞれの地域において,ある区間を走行した自動車の走行距離および走行時間から算出した値(以下,速度
という。単位は km/h)を用いる。
(1) 表 1 は,2015 年の交通量と速度の平均値,標準偏差および共分散である。ただし,共分散は交通量の偏差と速度の偏差の積の平均値である。
表1 2015 年の交通量と速度の平均値,標準偏差および共分散
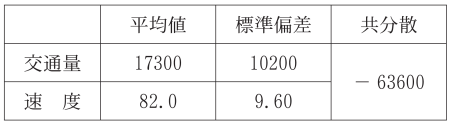
この表より,(標準偏差):(平均値)の比の値は,小数第 3 位を四捨五入すると,交通量については 0,59 であり,速度については $\boxed{\boxed{\textsf{テ}}}$ である。また,交通量と速度の相関係数は $\boxed{\boxed{\textsf{ト}}}$ である。
また,図 1 は,2015 年の交通量と速度の散布図である。なお,この散布図には,完全に重なっている点はない。
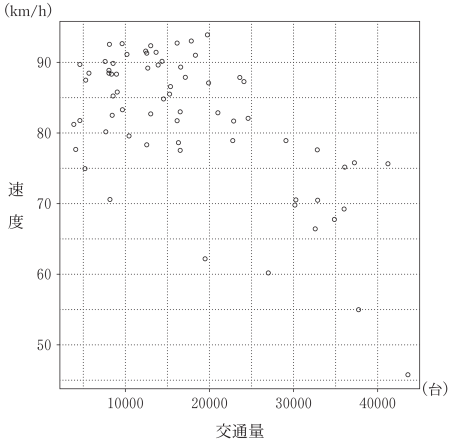
図1 2015年の交通量と速度の散布図
(出典:国土交通省の Web ページにより作成)
2015年の交通量のヒストグラムは,図 1 を参考にすると,$\boxed{\boxed{\textsf{ナ}}}$ である。なお,ヒストグラムの各階級の区間は,左側の数値を含み,右側の数値を含まない。また,表 1 および図 1 から読み取れることとして,後の $\text{\textcircled 0}$ ~ ⑤ のうち,正しいものは $\boxed{\boxed{\textsf{ニ}}}$ と $\boxed{\boxed{\textsf{ヌ}}}$ である。
$\boxed{\boxed{\text{テ}}}$,$\boxed{\boxed{\text{ト}}}$ については,最も適当なものを,次の $\text{\textcircled 0}$ ~ ⑨ のうちから一つずつ選べ。ただし,同じものを繰り返し選んでもよい。
$\text{\textcircled 0}$ $-0.71$ ① $-0.65$ ② $-0.59$
③ $-0.12$ ④ $-0.03$ ⑤ $0.03$
⑥ $0.12$ ⑦ $0.59$ ⑧ $0.65$
⑨ $0.71$
$\boxed{\boxed{\text{ナ}}}$ の解答群
$\boxed{\boxed{\text{ニ}}}$,$\boxed{\boxed{\text{ヌ}}}$ の解答群(解答の順序は問わない。)
$\text{\textcircled 0}$ 交通量が 27500 以上のすべての地域の速度は 75 未満である。
① 交通量が 10000 未満のすべての地域の速度は 70 以上である。
② 速度が平均値以上のすべての地域では,交通量が平均値以上である。
③ 速度が平均値未満のすべての地域では,交通量が平均値未満である。
④ 交通量が 27500 以上の地域は,ちょうど 7 地域存在する。
⑤ 速度が 72.5 未満の地域は,ちょうど 11 地域存在する。
(2) 図 2 は,2010 年と 2015 年の速度の散布図である。ただし,原点を通り,傾きが 1 である直線(点線)を補助的に描いている。また,この散布図には,完全に重なっている点はない。
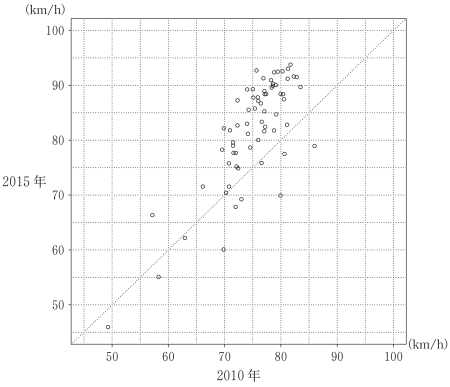
図2 2010 年と 2015 年の速度の散布図
(出典:国土交通省の Web ページにより作成)
67 地域について,2010 年より 2015 年の速度が速くなった地域群を A 群,遅くなった地域群を B 群とする。A 群の地域数は $\boxed{\textsf{ネノ}}$ である。 B 群において,2010 年より 2015 年の速度が,5 km/h 以上遅くなった地域数は $\boxed{\textsf{ハ}}$ であり,10 %以上遅くなった地域数は $\boxed{\textsf{ヒ}}$ である。
A 群の 2015 年の速度については,第 1 四分位数は 81.2,中央値は 86.7,第 3 四分位数は 89.7 であった。次の (I),(II),(III) は A 群と B 群の 2015 年の速度に関する記述である。
(I) A 群の速度の範囲は,B 群の速度の範囲より小さい。
(II) A 群の速度の第 1 四分位数は,B 群の速度の第 3 四分位数より小さい。
(III) A 群の速度の四分位範囲は,B 群の速度の四分位範囲より小さい。
(I),(II),(III) の正誤の組合せとして正しいものは $\boxed{\boxed{\textsf{フ}}}$ である。
$\boxed{\boxed{\text{フ}}}$ の解答群
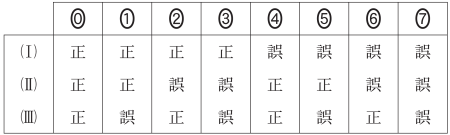
(3) 図 3 は 2015 年の速度の箱ひげ図である。図 4 は図 1 を再掲したものであり,2015 年の交通量と速度の散布図である。これらの速度から 1 km あたりの走行時間(分)を考える。例えば,速度が 55 km/h の場合は,1 時間あたりの走行距離が 55 km なので,1 km あたりの走行時間は $\cfrac{1}{55}\times60$ の小数第 3 位を四捨五入して 1.09 分となる。
このようにして 2015 年の速度を 1 km あたりの走行時間に変換したデータの箱ひげ図は $\boxed{\boxed{\textsf{ヘ}}}$ であり,2015 年の交通量と 1 km あたりの走行時間の散布図は $\boxed{\boxed{\textsf{ホ}}}$ である。なお,解答群の散布図には,完全に重なっている点はない。
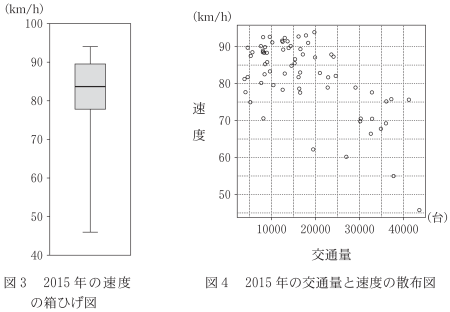
(出典:国土交通省の Web ページにより作成)
$\boxed{\boxed{\text{ヘ}}}$ の解答群
$\boxed{\boxed{\text{ホ}}}$ の解答群
SNSでシェア