【スマホで読む・わかりやすい】共通テスト数学IA2022追試【解説・正解・問題】
第1問 正解
ア,イ 3, 2 ウ 2
エ,オカ 6, 11 キ 5
ク,ケ,コ 1, 4, 7
サシ 36 ス 5 セ 4
ソ 6 タ,チ 4,3 ツ 4
テ 2 ト 5 ナ 7 ニ 8
〔1〕
(1)
$x\geqq c-\cfrac{1}{3}$ のとき,①の左辺は絶対値の中の式が正の値となるので,そのまま絶対値の記号を外して
$3x-3c+1=(3-\sqrt{3})x-1$ ・・・②
となる。これを変形すると
$3x-3c+1=3x-\sqrt{3}x-1$
$\sqrt{3}x=3x-2$
$x=\cfrac{3x-2}{\sqrt{3}}$
分母を有理化すると
$=\cfrac{3\sqrt{3}c-2\sqrt{3}}{3}$
$=\sqrt{3}c-\cfrac{2\sqrt{3}}{3}$ ・・・③
・・・ア,イ
次に ③ を $x\geqq c-\cfrac{1}{3}$ に代入すると
$\sqrt{3}c-\cfrac{2\sqrt{3}}{3}\geqq c-\cfrac{1}{3}$
$(\sqrt{3}-1)c\geqq-\cfrac{1}{3}+\cfrac{2\sqrt{3}}{3}$
$c\geqq\cfrac{-1+2\sqrt{3}}{3(\sqrt{3}-1)}$
分母を有理化すると
$c\geqq\cfrac{(-1+2\sqrt{3})(\sqrt{3}+1)}{3(\sqrt{3}-1)(\sqrt{3}+1)}$
$c\geqq\cfrac{-\sqrt{3}-1+6+2\sqrt{3}}{3(3-1)}$
$c\geqq\cfrac{5+\sqrt{3}}{6}$ ・・・(A)
・・・ウ
また,$x<c-\cfrac{1}{3}$ のとき,①の左辺は絶対値の中の式が負の値をとるので,符号を反対にして絶対値を外すと良い。
$-3x+3c-1=(3-\sqrt{3})x-1$ ・・・④
④を変形すると
$-3x+3c-1=3x-\sqrt{3}x-1$
$(\sqrt{3}-6)x=-3c$
$x=-\cfrac{3}{\sqrt{3}-6}\space c$
$=\cfrac{3}{6-\sqrt{3}}\space c$
分母を有理化すると
$=\cfrac{3(6+\sqrt{3})}{(6-\sqrt{3})(6+\sqrt{3})}\space c$
$=\cfrac{3(6+\sqrt{3})}{36-3}\space c$
$=\cfrac{3(6+\sqrt{3})}{33}\space c$
$=\cfrac{6+\sqrt{3}}{11}\space c$ ・・・⑤
・・・エ,,オカ
これを,$x<c-\cfrac{1}{3}$ に代入すると
$\cfrac{6+\sqrt{3}}{11}\space c<c-\cfrac{1}{3}$
$\Big(\cfrac{6+\sqrt{3}}{11}-1\Big)\space c<-\cfrac{1}{3}$
$\cfrac{6+\sqrt{3}-11}{11}\space c<-\cfrac{1}{3}$
$\cfrac{\sqrt{3}-5}{11}\space c<-\cfrac{1}{3}$
$\cfrac{5-\sqrt{3}}{11}\space c>\cfrac{1}{3}$
$c>\cfrac{11}{3(5-\sqrt{3})}$
分母を有理化すると
$c>\cfrac{11(5+\sqrt{3})}{3(5-\sqrt{3})(5+\sqrt{3})}$
$c>\cfrac{11(5+\sqrt{3})}{3(25-3)}$
$c>\cfrac{11(5+\sqrt{3})}{3\times22}$
$c>\cfrac{5+\sqrt{3}}{6}$ ・・・(B)
・・・キ
(2)
たとえば,$|x|=1$ ならば $x=\pm1$ となるように,方程式は絶対値の中が正の値となる場合と負の値になる場合で異なる二つの解をもつ。これを踏まえて,(A),(B)をもとに場合分けすると良い。
・ $c>\cfrac{5+\sqrt{3}}{6}$ のとき
これは (A) を満たすので ② はただ一つの解をもつ。
また,(B) も満たすので ④ はただ一つの解をもつ。
したがって,① は異なる二つの解をもつ。
・・・ク
・ $c=\cfrac{5+\sqrt{3}}{6}$ のとき
これは (A) を満たすので ② はただ一つの解をもつ。
一方で,これは (B) を満たさないので ④ は解をもたない。
よって,① はただ一つの解をもつ。
・・・ケ
・ $c<\cfrac{5+\sqrt{3}}{6}$ のとき
これは (A) も (B) も満たさないので①は解をもたない。
・・・コ
〔2〕
(1)
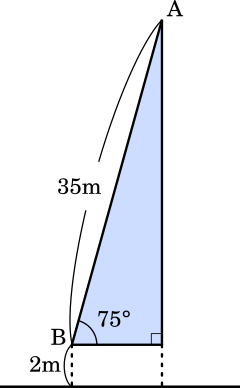
三角形の高さは,斜辺× $\sin$ で求めることができる。
$\sin=\cfrac{\textsf{高さ}}{\textsf{斜辺}}$ であることを利用すると
$\textsf{斜辺}\times\sin=\textsf{斜辺}\times\cfrac{\textsf{高さ}}{\textsf{斜辺}}$
$=\cancel{\textsf{斜辺}}\times\cfrac{\textsf{高さ}}{\cancel{\textsf{斜辺}}}$
$=\textsf{高さ}$
三角比の表を用いて
$35\times\sin75\degree=35\times0.9659$
$=33.8\cdots$
$\fallingdotseq34$
$34+2=36$ m
・・・サシ
(2)
(i)
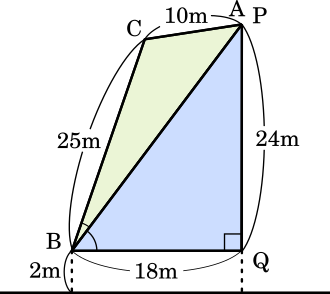
四角形を △ACB と △PBQ の二つに分け,∠PBQ と ∠ABC をそれぞれ求めると良い。
三平方の定理より
$\text{PB}^2=18^2+24^2$
$=900$
$\text{PB}=30$
$\tan\angle\text{PBQ}=\cfrac{24}{18}$
$=\cfrac{4}{3}=1.33\cdots$
三角比の表より,∠PBQ は約 53°。
△ACB について,余弦定理より
$10^2=25^2+30^2-2\times25\times30\cos\angle\text{ABC}$
$100=1525-1500\cos\angle\text{ABC}$
$1500\cos\angle\text{ABC}=1425$
$\cos\angle\text{ABC}=\cfrac{1425}{2500}$
$=\cfrac{19}{20}=0.95$
三角比の表より,∠ABC は約 18°。
したがって
$53+18=71\degree$
・・・ス
(ii)
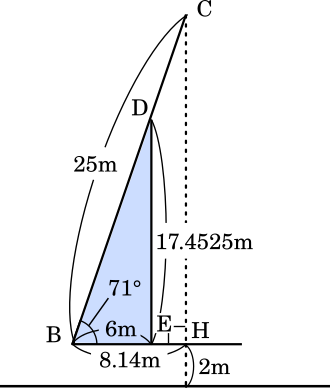
まず,フェンスを高くしていったときに BC にぶつかるのか AC にぶつかるのかを判断する。
$\textsf{斜辺}\times\cos=\cancel{\textsf{斜辺}}\times\cfrac{\textsf{底辺}}{\cancel{\textsf{斜辺}}}=\textsf{底辺}$
三角比の表より
$\text{BH}=25\times\cos71\degree$
$=25\times0.3256$
$=8.14$
よって,フェンスを高くしていくと BC にぶつかることが分かる。
次に DE の長さを求めると
$\textsf{底辺}\times\cos=\cancel{\textsf{底辺}}\times\cfrac{\textsf{高さ}}{\cancel{\textsf{底辺}}}=\textsf{高さ}$
三角比の表より
$\text{DE}=6\times\tan71\degree$
$=6\times2.9042$
$=17.4252$
よって,フェンスの高さが
$17.4252+2=19.4252$ m
のときにはしごに当たることになる。
したがって,はしごがフェンスに当たらずに,はしごの先端 A を点 P に一致させることができる最大のものは 19m である。
・・・セ
〔3〕
(1)
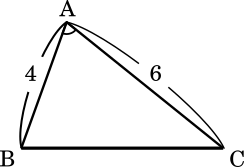
余弦定理より
$\text{BC}^2=4^2+6^2-2\times4\times6\cos\angle\text{BAC}$
$=52-48\times\cfrac{1}{3}$
$=52-16$
$=36$
$\text{BC}=6$
・・・ソ
(2)
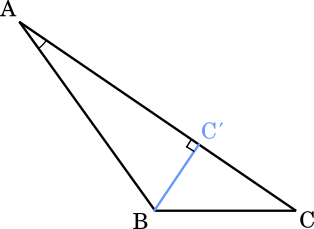
BC が最短になるのは ∠ACB が直角のときである。
このとき
$\text{BC}=4\times\sin\angle\text{BAC}$
$=4\times\cfrac{1}{3}=\cfrac{4}{3}$
したがって
$\text{BC}\geqq\cfrac{4}{3}$
・・・タ,チ
BC = $\cfrac{4}{3}$ のとき ∠ACB は直角となり,△ABC はただ一通りに決まる。
さらに $\text{BC}>\cfrac{4}{3}$ の場合は,以下のように$\sin\angle\text{BAC}=\cfrac{1}{3}$ となる △ABC は 2 通りあるので不適。
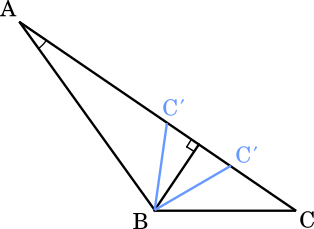
△ABC がただ一通りに決まるもう一つの場合は,△ACB が二等辺三角形になるときである。

直線 AC 上に B から引いた長さ 4 の直線は AB を除くと 1 つしか作ることができない。したがって,△ABC はただ一通りに定まる。
・・・ツ

$\sin$ は $\cfrac{\textsf{高さ}}{\textsf{斜辺}}$ だから
$\sin\angle\text{BAC}=\cfrac{1}{3}$
$\cfrac{\text{BC}}{\text{AC}}=\cfrac{1}{3}$
$\text{AC}=3\text{BC}$
また,三平方の定理より
$\text{BC}^2+4^2=\text{AC}^2$
$\text{BC}^2+4^2=9\text{BC}^2$
$8\text{BC}^2=16$
$\text{BC}^2=2$
$\text{BC}>0$ より
$\text{BC}=\sqrt{2}$
・・・テ
・$\cfrac{4}{3}<\text{BC}<\sqrt{2}$ のとき
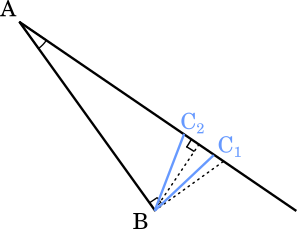
$\triangle\text{ABC}_1$ と $\triangle\text{ABC}_2$ の 2 つの三角形をつくることができる。
$\triangle\text{ABC}_1$ で考えると,$\angle\text{AC}_1\text{B}$ と $\angle\text{ABC}_1$ はともに鋭角だから,鋭角三角形である。
また,$\triangle\text{ABC}_2$ で考えると,$\angle\text{AC}_2\text{B}$ は鈍角だから,鈍角三角形である。
したがって,△ABC は二つに決まり,それらは鋭角三角形と鈍角三角形である。
・・・ト
・$\text{BC}=\sqrt{2}$ のとき

上の図のように,$\text{BC}=\sqrt{2}$ となる△ABC は二通りに決まり,それらは直角三角形と鈍角三角形である。
・・・ナ
・$\text{BC}>\sqrt{2}$ かつ $\text{BC}\not=4$ のとき
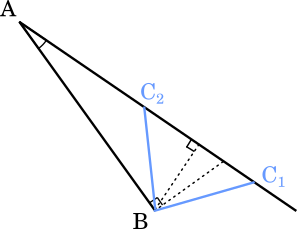
$\triangle\text{ABC}_1$ は $\angle\text{ABC}_1$ が鈍角であり,$\triangle\text{ABC}_2$ は $\angle\text{AC}_2\text{B}$ は鈍角である。
よって,△ABC は二通りに決まり,それらはともに鈍角三角形である。
・・・ニ
問題文
第1問
〔1〕 $c$ を実数とし,$x$ の方程式
$|3x-3c+1|=(3-\sqrt{3})x-1$ ・・・①
を考える。
(1) $x\geqq c-\cfrac{1}{3}$ のとき,①は
$3x-3c+1=(3-\sqrt{3})x-1$ ・・・②
となる。②を満たす $x$ は
$x=\sqrt{\boxed{\textsf{ア}}}\space c-\cfrac{\boxed{\textsf{イ}}\sqrt{3}}{3}$ ・・・③
となる。③が $x\geqq c-\cfrac{1}{3}$ を満たすような $c$ の値の範囲は $\boxed{\boxed{\textsf{ウ}}}$ である。
また,$x < c-\cfrac{1}{3}$ のとき,①は
$-3x+3c-1=(3-\sqrt{3})x-1$ ・・・④
となる。④を満たす $x$ は
$x=\cfrac{\boxed{\textsf{エ}}+\sqrt{3}}{\boxed{\textsf{オカ}}}\space c$ ・・・⑤
となる。⑤が $x<c-\cfrac{1}{3}$ を満たすような $c$ の値の範囲は $\boxed{\boxed{\textsf{キ}}}$ である。
$\boxed{\boxed{\textsf{ウ}}}$,$\boxed{\boxed{\textsf{キ}}}$ の解答群(同じものを繰り返し選んでもよい。)
$\text{\textcircled 0}$ $c\leqq\cfrac{3+\sqrt{3}}{6}$ ① $c<\cfrac{3-\sqrt{3}}{6}$
② $c\geqq\cfrac{5+\sqrt{3}}{6}$ ③ $c>\cfrac{3+\sqrt{3}}{6}$
④ $c\geqq\cfrac{3-\sqrt{3}}{6}$
⑤ $c>\cfrac{5+\sqrt{3}}{6}$
⑥ $c\leqq\cfrac{5-\sqrt{3}}{6}$ ⑦ $c\geqq\cfrac{7-3\sqrt{3}}{6}$
⑧ $c<\cfrac{5-\sqrt{3}}{6}$ ⑨ $c>\cfrac{7-3\sqrt{3}}{6}$
(2) ①が異なる二つの解をもつための必要十分条件は $\boxed{\boxed{\textsf{ク}}}$ であり,ただ一つの解をもつための必要十分条件は $\boxed{\boxed{\textsf{ケ}}}$ である。さらに,①が解をもたないための必要十分条件は $\boxed{\boxed{\textsf{コ}}}$ である。
$\boxed{\boxed{\textsf{ク}}}$ ~ $\boxed{\boxed{\textsf{コ}}}$ の解答群(同じものを繰り返し選んでもよい。)
$\text{\textcircled 0}$ $c>\cfrac{3-\sqrt{3}}{6}$ ① $c>\cfrac{5+\sqrt{3}}{6}$
② $c\geqq\cfrac{7-3\sqrt{3}}{6}$ ③ $c=\cfrac{3-\sqrt{3}}{6}$
④ $c=\cfrac{5+\sqrt{3}}{6}$
⑤ $c=\cfrac{7-3\sqrt{3}}{6}$
⑥ $c\leqq\cfrac{3-\sqrt{3}}{6}$ ⑦ $c<\cfrac{5+\sqrt{3}}{6}$
⑧ $c<\cfrac{7-3\sqrt{3}}{6}$
〔2〕 以下の問題を解答するにあたっては,必要に応じて 33 ページの三角比の表を用いてもよい。
火災時に,ビルの高層階に取り残された人を救出する際,はしご車を使用することがある。
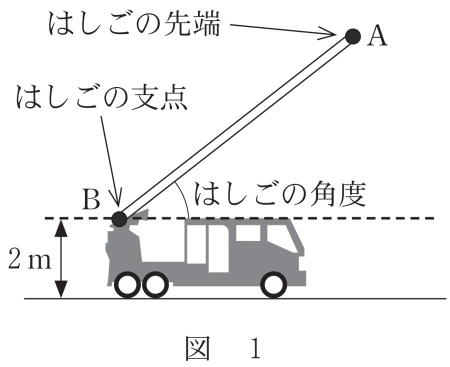
図1のはしご車で考える。はしごの先端を A,はしごの支点を B とす る。はしごの角度(はしごと水平面のなす角の大きさ)は 75° まで大きくすることができ,はしごの長さ AB は 35m まで伸ばすことができる。また,はしごの支点 B は地面から 2 m の高さにあるとする。
以下,はしごの長さ AB は 35m に固定して考える。また,はしごは太さを無視して線分とみなし,はしご車は水平な地面上にあるものとする。
(1) はしごの先端 A の最高到達点の高さは,地面から $\boxed{\textsf{サシ}}$ サシ m である。小数第 1 位を四捨五入して答えよ。
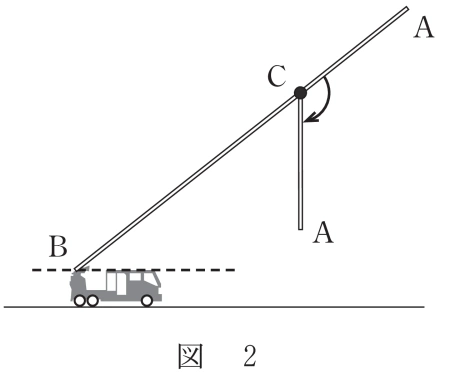
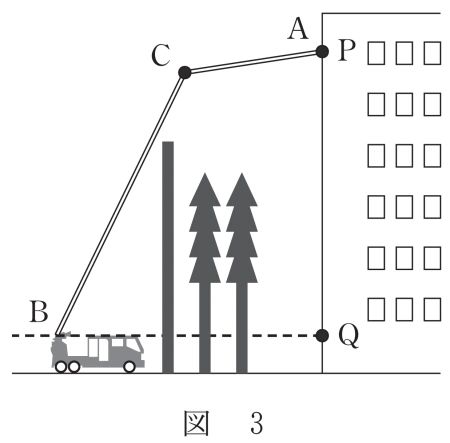
(2) 図 1 のはしごは,図 2 のように,点 C で,AC が鉛直方向になるまで下 向きに屈折させることができる。AC の長さは 10m である。 図 3 のように,あるビルにおいて,地面から 26m の高さにある位置を 点 P とする。障害物のフェンスや木があるため,はしご車を BQ の長さが 18m となる場所にとめる。ここで,点 Q は,点 P の真下で,点 B と同じ高さにある位置である。
このとき,はしごの先端 A が点 P に届くかどうかは,障害物の高さや,はしご車と障害物の距離によって決まる。そこで,このことについて,後の (i),(ii) のように考える。
ただし,はしご車,障害物,ビルは同じ水平な地面上にあり,点 A, B,C,P,Q はすべて同一平面上にあるものとする。
(i) はしごを点 C で屈折させ,はしごの先端 A が点 P に一致したとする と,∠QBC の大きさはおよそ $\boxed{\boxed{\textsf{ス}}}$° になる。
$\boxed{\boxed{\textsf{ス}}}$ については,最も適当なものを,次の $\text{\textcircled 0}$ ~ ⑥のうちから一つ選べ。
$\text{\textcircled 0}$ 53 ① 56 ② 59 ③ 63
④ 67 ⑤ 71 ⑥ 75
(ii) はしご車に最も近い障害物はフェンスで,フェンスの高さは 7m 以上あり,障害物の中で最も高いものとする。フェンスは地面に垂直で点 B,Q の間にあり,フェンスと BQ との交点から点 B までの距離は 6m である。また,フェンスの厚みは考えないとする。
このとき,次の $\text{\textcircled 0}$ ~ ⑥ のフェンスの高さのうち,図 3 のように,はしごがフェンスに当たらずに,はしごの先端 A を点 P に一致させることができる最大のものは,$\boxed{\boxed{\textsf{セ}}}$ である。
$\boxed{\boxed{\textsf{セ}}}$ の解答群
$\text{\textcircled 0}$ 7m ① 10m ② 13m ③ 16m
④ 19m ⑤ 22m ⑥ 25m
三角比の表
| 角 | 正弦(sin) | 余弦(cos) | 正接(tan) |
|---|---|---|---|
| 0° | 0.0000 | 1.0000 | 0.0000 |
| 1° | 0.0175 | 0.9998 | 0.0175 |
| 2° | 0.0349 | 0.9994 | 0.0349 |
| 3° | 0.0523 | 0.9986 | 0.0524 |
| 4° | 0.0698 | 0.9976 | 0.0699 |
| 5° | 0.0872 | 0.9962 | 0.0875 |
| 6° | 0.1045 | 0.9945 | 0.1051 |
| 7° | 0.1219 | 0.9925 | 0.1228 |
| 8° | 0.1392 | 0.9903 | 0.1405 |
| 9° | 0.1564 | 0.9877 | 0.1584 |
| 10° | 0.1736 | 0.9848 | 0.1763 |
| 11° | 0.1908 | 0.9816 | 0.1944 |
| 12° | 0.2079 | 0.9781 | 0.2126 |
| 13° | 0.2250 | 0.9744 | 0.2309 |
| 14° | 0.2419 | 0.9703 | 0.2493 |
| 15° | 0.2588 | 0.9659 | 0.2679 |
| 16° | 0.2756 | 0.9613 | 0.2867 |
| 17° | 0.2924 | 0.9563 | 0.3057 |
| 18° | 0.3090 | 0.9511 | 0.3249 |
| 19° | 0.3256 | 0.9455 | 0.3443 |
| 20° | 0.3420 | 0.9397 | 0.3640 |
| 21° | 0.3584 | 0.9336 | 0.3839 |
| 22° | 0.3746 | 0.9272 | 0.4040 |
| 23° | 0.3907 | 0.9205 | 0.4245 |
| 24° | 0.4067 | 0.9135 | 0.4452 |
| 25° | 0.4226 | 0.9063 | 0.4663 |
| 26° | 0.4384 | 0.8988 | 0.4877 |
| 27° | 0.4540 | 0.8910 | 0.5095 |
| 28° | 0.4695 | 0.8829 | 0.5317 |
| 29° | 0.4848 | 0.8746 | 0.5543 |
| 30° | 0.5000 | 0.8660 | 0.5774 |
| 31° | 0.5150 | 0.8572 | 0.6009 |
| 32° | 0.5299 | 0.8480 | 0.6249 |
| 33° | 0.5446 | 0.8387 | 0.6494 |
| 34° | 0.5592 | 0.8290 | 0.6745 |
| 35° | 0.5736 | 0.8192 | 0.7002 |
| 36° | 0.5878 | 0.8090 | 0.7265 |
| 37° | 0.6018 | 0.7986 | 0.7536 |
| 38° | 0.6157 | 0.7880 | 0.7813 |
| 39° | 0.6293 | 0.7771 | 0.8098 |
| 40° | 0.6428 | 0.7660 | 0.8391 |
| 41° | 0.6561 | 0.7547 | 0.8693 |
| 42° | 0.6691 | 0.7431 | 0.9004 |
| 43° | 0.6820 | 0.7314 | 0.9325 |
| 44° | 0.6947 | 0.7193 | 0.9657 |
| 45° | 0.7071 | 0.7071 | 1.0000 |
| 46° | 0.7193 | 0.6947 | 1.0355 |
| 47° | 0.7314 | 0.6820 | 1.0724 |
| 48° | 0.7431 | 0.6691 | 1.1106 |
| 49° | 0.7547 | 0.6561 | 1.1504 |
| 50° | 0.7660 | 0.6428 | 1.1918 |
| 51° | 0.7771 | 0.6293 | 1.2349 |
| 52° | 0.7880 | 0.6157 | 1.2799 |
| 53° | 0.7986 | 0.6018 | 1.3270 |
| 54° | 0.8090 | 0.5878 | 1.3764 |
| 55° | 0.8192 | 0.5736 | 1.4281 |
| 56° | 0.8290 | 0.5592 | 1.4826 |
| 57° | 0.8387 | 0.5446 | 1.5399 |
| 58° | 0.8480 | 0.5299 | 1.6003 |
| 59° | 0.8572 | 0.5150 | 1.6643 |
| 60° | 0.8660 | 0.5000 | 1.7321 |
| 61° | 0.8746 | 0.4848 | 1.8040 |
| 62° | 0.8829 | 0.4695 | 1.8807 |
| 63° | 0.8910 | 0.4540 | 1.9626 |
| 64° | 0.8988 | 0.4384 | 2.0503 |
| 65° | 0.9063 | 0.4226 | 2.1445 |
| 66° | 0.9135 | 0.4067 | 2.2460 |
| 67° | 0.9205 | 0.3907 | 2.3559 |
| 68° | 0.9272 | 0.3746 | 2.4751 |
| 69° | 0.9336 | 0.3584 | 2.6051 |
| 70° | 0.9397 | 0.3420 | 2.7475 |
| 71° | 0.9455 | 0.3256 | 2.9042 |
| 72° | 0.9511 | 0.3090 | 3.0777 |
| 73° | 0.9563 | 0.2924 | 3.2709 |
| 74° | 0.9613 | 0.2756 | 3.4874 |
| 75° | 0.9659 | 0.2588 | 3.7321 |
| 76° | 0.9703 | 0.2419 | 4.0108 |
| 77° | 0.9744 | 0.2250 | 4.3315 |
| 78° | 0.9781 | 0.2079 | 4.7046 |
| 79° | 0.9816 | 0.1908 | 5.1446 |
| 80° | 0.9848 | 0.1736 | 5.6713 |
| 81° | 0.9877 | 0.1564 | 6.3138 |
| 82° | 0.9903 | 0.1392 | 7.1154 |
| 83° | 0.9925 | 0.1219 | 8.1443 |
| 84° | 0.9945 | 0.1045 | 9.5144 |
| 85° | 0.9962 | 0.0872 | 11.4301 |
| 86° | 0.9976 | 0.0698 | 14.3007 |
| 87° | 0.9986 | 0.0523 | 19.0811 |
| 88° | 0.9994 | 0.0349 | 28.6363 |
| 89° | 0.9998 | 0.0175 | 57.2900 |
| 90° | 1.0000 | 0.0000 | – |
〔3〕 三角形は,与えられた辺の長さや角の大きさの条件によって,ただ一通りに決まる場合や二通りに決まる場合がある。
以下,△ABC において AB = 4 とする。
(1) AC = 6,cos ∠BAC = $\cfrac{1}{3}$ とする。このとき BC = $\boxed{\textsf{ソ}}$ であり,△ABC はただ一通りに決まる。
(2) sin ∠BAC = $\cfrac{1}{3}$ とする。このとき,BC の長さのとり得る値の範囲は,点 B と直線 AC との距離を考えることにより,BC ≧ $\cfrac{\enspace\boxed{\textsf{タ}}\enspace}{\boxed{\textsf{チ}}}$ である。
BC = $\cfrac{\enspace\boxed{\textsf{タ}}\enspace}{\boxed{\textsf{チ}}}$
または BC = $\boxed{\textsf{ツ}}$ のとき,△ABC はただ一通りに決まる。
また,∠ABC = 90° のとき,BC = $\sqrt{\boxed{\textsf{テ}}}$ である。
したがって,△ABC の形状について,次のことが成り立つ。
・$\cfrac{\enspace\boxed{\textsf{タ}}\enspace}{\boxed{\textsf{チ}}}$ < BC < $\sqrt{\boxed{\textsf{テ}}}$ のとき,△ ABC は $\boxed{\boxed{\textsf{ト}}}$。
・BC = $\sqrt{\boxed{\textsf{テ}}}$ のとき,△ABC は $\boxed{\boxed{\textsf{ナ}}}$。
・BC > $\sqrt{\boxed{\textsf{テ}}}$ かつ BC $\not=$ $\boxed{\boxed{\textsf{ツ}}}$ のとき,△ABC は $\boxed{\boxed{\textsf{ニ}}}$。
$\boxed{\boxed{\text{ト}}}$ ~ $\boxed{\boxed{\text{ニ}}}$ の解答群(同じものを繰り返し選んでもよい。)
$\text{\textcircled 0}$ ただ一通りに決まり,それは鋭角三角形である
① ただ一通りに決まり,それは直角三角形である
② ただ一通りに決まり,それは鈍角三角形である
③ 二通りに決まり,それらはともに鋭角三角形である
④ 二通りに決まり,それらは鋭角三角形と直角三角形である
⑤ 二通りに決まり,それらは鋭角三角形と鈍角三角形である
⑥ 二通りに決まり,それらはともに直角三角形である
⑦ 二通りに決まり,それらは直角三角形と鈍角三角形である
⑧ 二通りに決まり,それらはともに鈍角三角形である
SNSでシェア