【確率】数直線上を移動する動点と確率(千葉大2019第12問)

数直線上に動点 P があり，はじめに原点にあるとする。$k=1,2,\cdots$ に対し，$k$ 回目にさいころを振ったとき，1, 2 の目が出たら P は正の方向に $\cfrac{1}{2^k}$ だけ移動し，3, 4 が出たら負の方向に $\cfrac{1}{2^k}$ だけ移動し，5, 6 が出たら移動しないとする。$n$ 回さいころを振った後の点 P の座標を $X_n$ とする。

(1) $0<X_n$ となる確率を求めよ。

(2) $\cfrac{1}{2}<X_n$ となる確率を求めよ。

(3) $\ell$ は $n$ 未満の正の整数とする。このとき，$\cfrac{1}{2^\ell}<X_n$ となる確率を求めよ。

分数どうしを比べる

(1) $0<X_n$ となる確率を求めよ。

まず，数直線上の移動は，負の向き，0，正の向きの 3 つに分けて考えることができます。

いったん 0 を除いて考えると，たとえば

$+\cfrac{1}{2},-\cfrac{1}{2^2},-\cfrac{1}{2^3},+\cfrac{1}{2^4},-\cfrac{1}{2^5},\cdots$

のように移動していきます。これらの総和が $X_n$ です。

$X_n=\cfrac{1}{2}-\cfrac{1}{4}-\cfrac{1}{8}+\cfrac{1}{16}-\cfrac{1}{32}+\cdots+\cfrac{1}{2^n}$

こうして見てみると，正にしろ負にしろ移動する量は次第に小さくなっていき 0 に近づいていくことが分かります。

もし，すべて正の場合はどうでしょうか？

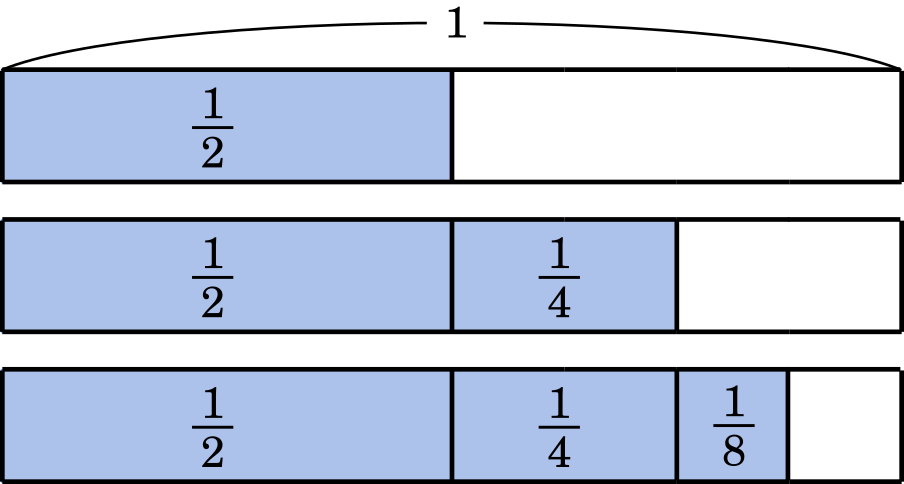
1 の半分が $\cfrac{1}{2}$，$\cfrac{1}{2}$ を除いた部分の半分が $\cfrac{1}{4}$，さらにその半分が $\cfrac{1}{8}$，…と続いていくので，ひたすら足していっても 1 を超えることない，ということがイメージできると思います。

また，上の図から $\cfrac{1}{2}$ は $\cfrac{1}{4}+\cfrac{1}{8}$ よりも大きく，それを $\cfrac{1}{4}+\cfrac{1}{8}+\cfrac{1}{16}+\cfrac{1}{32}+\cdots$ としてもやはり $\cfrac{1}{2}$ の方が大きくなります。

つまり

$\cfrac{1}{2}>\cfrac{1}{2^2}+\cfrac{1}{2^3}+\cfrac{1}{2^4}+\cdots+\cfrac{1}{2^n}$

が成り立ちそうです。

ここで，解法が見えてきます。もし 1 回目が $+\cfrac{1}{2}$ であれば，2 回目以降がすべて負であったとしても，合計は正の値になります。

$\cfrac{1}{2}-\Big(\cfrac{1}{2^2}+\cfrac{1}{2^3}+\cfrac{1}{2^4}+\cdots+\cfrac{1}{2^n}\Big)>0$

つまり，1 回目が正なら，2 回目以降は負，0，正のいずれであろうが，$X_n>0$ が成り立つのです。

また，反対に 1 回目が負なら合計は負の値になるので除外します。

では，1 回目が 0 のときはどうでしょうか？ 1 回目が 0 で 2 回目が $+\cfrac{1}{2^2}$ だったとしても，上と同じような話が成り立ちます。

$\cfrac{1}{2^2}-\Big(\cfrac{1}{2^3}+\cfrac{1}{2^4}+\cfrac{1}{2^5}+\cdots+\cfrac{1}{2^n}\Big)>0$

これを進めていくと，はじめ 0 が続いて，0，0，0,…，正，…の場合は $X_n>0$ が成り立つわけです。

ここから，はじめ 0 が続き，$m$ 回目で正になる場合，$X_n>0$ が成り立つことを示していきます。

$\cfrac{1}{2^m}-\Big(\cfrac{1}{2^{m+1}}+\cfrac{1}{2^{m+2}}+\cfrac{1}{2^{m+3}}+\cdots+\cfrac{1}{2^n}\Big)$
$\displaystyle=\cfrac{1}{2^m}-\sum_{k=m+1}^n\cfrac{1}{2^k}$

シグマの部分はこのまま計算しても良いのですが，念のため 2 つに分けておきます。

$\displaystyle=\cfrac{1}{2^m}-\Big(\sum_{k=1}^n\cfrac{1}{2^k}-\sum_{k=1}^m\cfrac{1}{2^k}\Big)$

シグマの部分は等比数列の総和だから，公式を用いて

$\displaystyle=\cfrac{1}{2^m}-\cfrac{\cfrac{1}{2}\Big\{1-\Big(\cfrac{1}{2}\Big)^n\Big\}}{1-\cfrac{1}{2}}+\cfrac{\cfrac{1}{2}\Big\{1-\Big(\cfrac{1}{2}\Big)^m\Big\}}{1-\cfrac{1}{2}}$
$=\cfrac{1}{2^m}-1+\cfrac{1}{2^n}+1-\cfrac{1}{2^m}$
$=\cfrac{1}{2^n}>0$

こうして，はじめ 0 が続き，$m$ 回目で正になる確率は

$\underbrace{\cfrac{1}{3}\cdot\cfrac{1}{3}\cdot\cfrac{1}{3}}_{1\cdots m-1\textsf{回目}}\cdots\underbrace{\cfrac{1}{3}}_{m\textsf{回目}}=\Big(\cfrac{1}{3}\Big)^m$

$m=1$ ならば，1 回目が正の場合となります。

あとは

正
0，正
0，0，正
0，0，0，正
$\vdots$

の場合を足し合わせていけばよいので，求める確率は

$\displaystyle\sum_{k=1}^n\Big(\cfrac{1}{3}\Big)^k$

これも等比数列の総和だから

$=\cfrac{\cfrac{1}{3}\Big\{1-\Big(\cfrac{1}{3}\Big)^n\Big\}}{1-\cfrac{1}{3}}$
$=\cfrac{\cfrac{1}{3}\Big\{1-\Big(\cfrac{1}{3}\Big)^n\Big\}}{\cfrac{2}{3}}$
$=\cfrac{1}{2}\Big\{1-\Big(\cfrac{1}{3}\Big)^n\Big\}$　（答え）

〔別解〕

この問題は余事象でも考えられます。結局，すべて 0 のときを除けば総和は正か負のどちらかであり，その確率はどちらも同じになります。よって，全事象からすべて 0 の場合を引いて 2 で割っても答えが出ます。

$\Big\{1-\Big(\cfrac{1}{3}\Big)^n\Big\}\div2$
$=\cfrac{1}{2}\Big\{1-\Big(\cfrac{1}{3}\Big)^n\Big\}$　（答え）

1 回目と 2 回目を考える

(2) $\cfrac{1}{2}<X_n$ となる確率を求めよ。

1 回目が負だと，$X_n<0$ となるのでアウトです。また，1 回目が 0 の場合はどうでしょうか？(1)の考察を踏まえれば，2 回目以降がすべて正だとしても

$\cfrac{1}{2^2}+\cfrac{1}{2^3}+\cfrac{1}{2^4}+\cdots+\cfrac{1}{2^n}<\cfrac{1}{2}$

となるので，やはりアウトです。

となると，条件は 1 回目が $+\cfrac{1}{2}$ であることです。そして，2 ～ $n$ 回目の総和が正の値なら $\cfrac{1}{2}<X_n$ が成り立つことになります。

もし 2 回目が負だと 3 ～ $n$ 回目がすべて正でも 2 ～ $n$ 回目の総和は負の値になります。つまり，2 回目は 0 か正でなければなりません。

2 回目が 0 の場合，3 回目が正なら 3 ～ $n$ 回目の総和が正になるので，当然，2 ～ $n$ 回目の総和も正です。ここも(1)の考察と同じで，2 回目以降 0 が続いて，0，0，…，正，…のパターンは 2 ～ $n$ 回目の総和が正の値になるわけです。

(1)で求めたように，1 ～ $n$ 回目が，0，0，…，正となる確率は

$\cfrac{1}{2}\Big\{1-\Big(\cfrac{1}{3}\Big)^n\Big\}$

だったので，2 ～ $n$ 回目が，0，0，…，正，…となる確率は

$\cfrac{1}{2}\Big\{1-\Big(\cfrac{1}{3}\Big)^{n-1}\Big\}$

となります。1 回目が $+\cfrac{1}{2}$ になる確率は $\cfrac{1}{3}$ だから，求める確率は

$\cfrac{1}{3}\cdot\cfrac{1}{2}\Big\{1-\Big(\cfrac{1}{3}\Big)^n\Big\}$
$=\cfrac{1}{6}\Big\{1-\Big(\cfrac{1}{3}\Big)^n\Big\}$　（答え）

考察をさらに発展させる

(3) $\ell$ は $n$ 未満の正の整数とする。このとき，$\cfrac{1}{2^{\ell}}<X_n$ となる確率を求めよ。

(2)の考察をさらに進めていきましょう。

もし 1 回目が負だと，それ以降が全部正でも総和は負の値です。やはり条件は，はじめが正であるか，0，0，…，正，…のパターンです。

たとえば，$m$ 回目で正，そのあと $\ell$ 回目まで負が続くとすると

$\cfrac{1}{2^m}-\Big(\cfrac{1}{2^{m+1}}+\cfrac{1}{2^{m+2}}+\cfrac{1}{2^{m+3}}+\cdots+\cfrac{1}{2^\ell}\Big)$
$\displaystyle=\cfrac{1}{2^m}-\sum_{k=m+1}^\ell\cfrac{1}{2^k}$
$\displaystyle=\cfrac{1}{2^m}-\sum_{k=1}^\ell\cfrac{1}{2^k}+\sum_{k=1}^m\cfrac{1}{2^k}$
$=\cfrac{1}{2^m}-\cfrac{\cfrac{1}{2}\Big\{1-\Big(\cfrac{1}{2}\Big)^\ell\Big\}}{1-\cfrac{1}{2}}+\cfrac{\cfrac{1}{2}\Big\{1-\Big(\cfrac{1}{2}\Big)^m\Big\}}{1-\cfrac{1}{2}}$
$=\cfrac{1}{2^m}-1+\cfrac{1}{2^\ell}+1-\cfrac{1}{2^m}$
$=\cfrac{1}{2^\ell}$

となるので，$\ell$ 回目までの総和は $\cfrac{1}{2^\ell}$ です。
言い換えれば，0，0，が続いたあと，$\ell$ 回目で $\cfrac{1}{2^\ell}$ が出るパターンと同じということです。そしてこのあと，0，0，正，…のパターンが来ると，$\cfrac{1}{2^\ell}<X_n$ が成り立ちます。

つまり

$0,0,\cdots,\underbrace{\cfrac{1}{2^m}}_{m\textsf{回目}},\underbrace{\textsf{負},\textsf{負},\cdots}_{m+1\cdots\ell\textsf{回目}},\underbrace{0,0,\cdots,\textsf{正},\cdots}_{\ell+1\cdots n\textsf{回目}}$

この場合，確率は

$\underbrace{\Big(\cfrac{1}{3}\Big)^{m-1}}_{1\cdots m-1\textsf{回目}}\cdot\underbrace{\cfrac{1}{3}}_{m\textsf{回目}}\cdot\underbrace{\Big(\cfrac{1}{3}\Big)^{\ell-m}}_{m+1\cdots\ell\textsf{回目}}\cdot\underbrace{\cfrac{1}{2}\Big\{1-\Big(\cfrac{1}{3}\Big)^{n-\ell}\Big\}}_{\ell+1\cdots n\textsf{回目}}$

これが，$m=1$ から $m=\ell$ までそれぞれあるので

$\displaystyle\sum_{k=1}^\ell\Big(\cfrac{1}{3}\Big)^{m-1}\cdot\cfrac{1}{3}\cdot\Big(\cfrac{1}{3}\Big)^{\ell-m}\cdot\cfrac{1}{2}\Big\{1-\Big(\cfrac{1}{3}\Big)^{n-\ell}\Big\}$
$\displaystyle=\sum_{k=1}^\ell\Big(\cfrac{1}{3}\Big)^\ell\cdot\cfrac{1}{2}\Big\{1-\Big(\cfrac{1}{3}\Big)^{n-\ell}\Big\}$
$\displaystyle=\sum_{k=1}^\ell\cfrac{1}{2}\Big(\cfrac{1}{3}\Big)^\ell-\cfrac{1}{2}\Big(\cfrac{1}{3}\Big)^n$

これ以外のパターンはどうなるでしょうか？

0，0, …のあと $m$ 回目で $+\cfrac{1}{2^m}$ が出て，$m+1\cdots\ell$ 回目が「すべて負」以外であれば，上の考察より $\ell$ 回目の時点で，総和は $\cfrac{1}{2^\ell}$ より大きくなります。

$\cfrac{1}{2^\ell}$ より大きくなるもののうち，最も小さいものは

$0,0,\cdots,\underbrace{\cfrac{1}{2^m}}_{m\textsf{回目}},\underbrace{\textsf{負},\textsf{負},\cdots}_{m+1\cdots\ell-1\textsf{回目}},\underbrace{0}_{\ell\textsf{回目}}$

があります。この場合

$\cfrac{1}{2^m}-\Big(\cfrac{1}{2^{m+1}}+\cfrac{1}{2^{m+2}}+\cdots+\cfrac{1}{2^{\ell-1}}\Big)$
$\displaystyle=\cfrac{1}{2^m}-\sum_{k=m+1}^{\ell-1}\cfrac{1}{2^k}$
$\displaystyle=\cfrac{1}{2^m}-\sum_{k=1}^{\ell-1}\cfrac{1}{2^k}+\sum_{k=1}^m\cfrac{1}{2^k}$
$=\cfrac{1}{2^m}-1+\cfrac{1}{2^{\ell-1}}+1-\cfrac{1}{2^m}$
$=\cfrac{2}{2^{\ell}}$

となります。よって，正確には $\cfrac{2}{2^{\ell}}$ より大きい，ということです。

この状態で，$\ell+1\cdots n$ 回目がすべて負であったとしても，総和は

$\cfrac{2}{2^\ell}-\displaystyle\sum_{k=\ell+1}^n\cfrac{1}{2^k}$
$=\cfrac{2}{2^\ell}-1+\cfrac{1}{2^n}+1-\cfrac{1}{2^\ell}$
$=\cfrac{1}{2^\ell}+\cfrac{1}{2^n}$

となるので，$\cfrac{1}{2^\ell}<X_n$ が成り立ちます。よって，$\ell+1$ 回目以降は負，0，正のいずれでも構わないことになります。

0，0, …のあと $m$ 回目で $+\cfrac{1}{2^m}$ が出て，$m+1\cdots\ell$ 回目が「すべて負」以外となる確率は

$\displaystyle\sum_{k=1}^\ell\Big(\cfrac{1}{3}\Big)^{k-1}\cdot\cfrac{1}{3}\cdot\Big\{1-\Big(\cfrac{1}{3}\Big)^{\ell-k}\Big\}$
$\displaystyle=\sum_{k=1}^\ell\Big(\cfrac{1}{3}\Big)^k\Big\{1-\Big(\cfrac{1}{3}\Big)^{\ell-k}\Big\}$
$\displaystyle=\sum_{k=1}^\ell\Big(\cfrac{1}{3}\Big)^k-\Big(\cfrac{1}{3}\Big)^\ell$

となります。

2 つを合わせると

$\displaystyle\sum_{k=1}^\ell\cfrac{1}{2}\Big(\cfrac{1}{3}\Big)^\ell-\cfrac{1}{2}\Big(\cfrac{1}{3}\Big)^n+\sum_{k=1}^\ell\Big(\cfrac{1}{3}\Big)^k-\Big(\cfrac{1}{3}\Big)^\ell$
$\displaystyle=\sum_{k=1}^\ell\Big(\cfrac{1}{3}\Big)^k-\cfrac{1}{2}\Big(\cfrac{1}{3}\Big)^\ell-\cfrac{1}{2}\Big(\cfrac{1}{3}\Big)^n$
$=\cfrac{\cfrac{1}{3}\Big\{1-\Big(\cfrac{1}{3}\Big)^\ell\Big\}}{1-\cfrac{1}{3}}-\cfrac{\ell}{2}\Big(\cfrac{1}{3}\Big)^\ell-\cfrac{\ell}{2}\Big(\cfrac{1}{3}\Big)^n$
$=\cfrac{1}{2}\Big\{1-\Big(\cfrac{1}{3}\Big)^\ell\Big\}-\cfrac{\ell}{2}\Big(\cfrac{1}{3}\Big)^\ell-\cfrac{\ell}{2}\Big(\cfrac{1}{3}\Big)^n$
$=\cfrac{1}{2}-\cfrac{1}{2}\Big(\cfrac{1}{3}\Big)^\ell-\cfrac{\ell}{2}\Big(\cfrac{1}{3}\Big)^\ell-\cfrac{\ell}{2}\Big(\cfrac{1}{3}\Big)^n$
$=\cfrac{1}{2}-\cfrac{1+\ell}{2}\Big(\cfrac{1}{3}\Big)^\ell-\cfrac{\ell}{2}\Big(\cfrac{1}{3}\Big)^n$　（答え）