【スマホで読む・わかりやすい】共通テスト数学IIB2022本試【解説・正解・問題】

第５問　正解

アイ,ウ -2, 3　エ,オ 1, 0
カ,キ 4,0　ク,ケ 3,5
コ,サ,シ 3,5,3　ス 3　セ 0
ソ 6　タ -　チ,ツ 2,3　テ,ト 3, 4

(1)

まず，$\overrightarrow{\text{OC}}=-\overrightarrow{\text{OA}}$ より，$\overrightarrow{\text{OC}}$ は $\overrightarrow{\text{OA}}$ と反対向きで同じ長さだから，AC は円の直径となる。

$\cos\angle\text{AOB}$ を求めるには内積の公式を用いて

$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=|\overrightarrow{\text{OA}}||\overrightarrow{\text{OB}}|\cos\angle\text{AOB}$

$\cos\angle\text{AOB}=\cfrac{\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}}{|\overrightarrow{\text{OA}}|\cdot|\overrightarrow{\text{OB}}|}$

$|\overrightarrow{\text{OA}}|=1$，$|\overrightarrow{\text{OB}}|=1$，$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=-\cfrac{2}{3}$ だから

$\cos\angle\text{AOB}=\cfrac{-\cfrac{2}{3}}{1\cdot1}=\cfrac{-2}{3}$

・・・アイ,ウ

点 P は AB の内分点だから

$\overrightarrow{\text{OP}}=(1-t)\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$

よって

$\overrightarrow{\text{OQ}}=k\overrightarrow{\text{OP}}$
$=k(1-t)\overrightarrow{\text{OA}}+kt\overrightarrow{\text{OB}}$
$=(k-kt)\overrightarrow{\text{OA}}+kt\overrightarrow{\text{OB}}$ ・・・①

・・・エ,オ

$\overrightarrow{\text{CQ}}=\overrightarrow{\text{OQ}}-\overrightarrow{\text{OC}}$
$=\overrightarrow{\text{OQ}}-(-\overrightarrow{\text{OA}})$
$=\overrightarrow{\text{OQ}}+\overrightarrow{\text{OA}}$
$=(k-kt+1)\overrightarrow{\text{OA}}+kt\overrightarrow{\text{OB}}$

・・・カ,キ

$\overrightarrow{\text{OA}}$ と $\overrightarrow{\text{OP}}$ が垂直となるとき

$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OP}}=0$ が成り立つ。

$\overrightarrow{\text{OA}}\cdot\{(1-t)\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}\}=0$
$(1-t)|\overrightarrow{\text{OA}}|^2+t\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=0$
$1-t-\cfrac{2}{3}t=0$
$\cfrac{5}{3}t=1$
$t=\cfrac{3}{5}$

・・・ク,ケ

(2)

∠OCQ が直角であるから

$\overrightarrow{\text{CO}}\cdot\overrightarrow{\text{CQ}}=0$

が成り立つ。

$(-\overrightarrow{\text{OC}})\cdot\overrightarrow{\text{CQ}}=0$
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{CQ}}=0$
$\overrightarrow{\text{OA}}\{(k-kt+1)\overrightarrow{\text{OA}}+kt\overrightarrow{\text{OB}}\}=0$
$(k-ky+1)|\overrightarrow{\text{OA}}|^2+kt\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=0$
$k-kt+1-\cfrac{2}{3}kt=0$
$k-\cfrac{5}{3}kt+1=0$
$3k-5kt+3=0$
$k(3-5t)=-3$
$k(5t-3)=3$
$k=\cfrac{3}{5t-3}$ ・・・②

・・コ,サ,シ

次に，領域の分け方は以下の図のようになる。

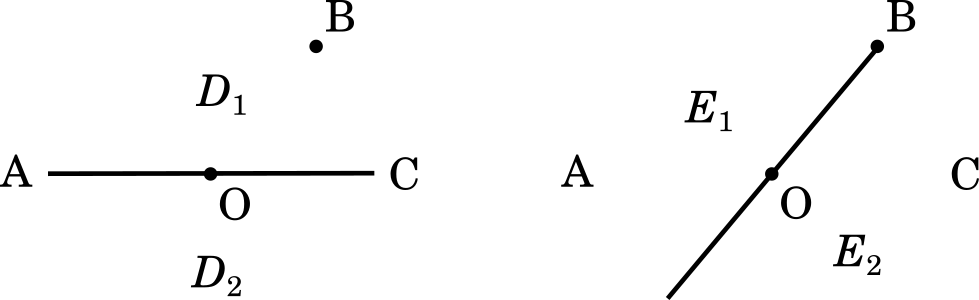
また，$t=\cfrac{3}{5}$ のとき，∠AOP は直角になることをふまえると

・$0<t<\cfrac{3}{5}$ のとき

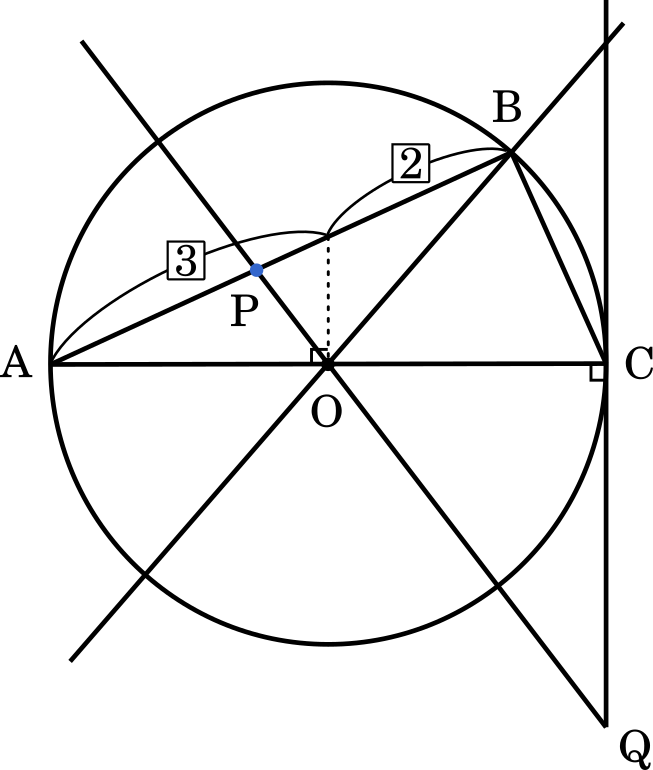
点 Q は $D_2$ に含まれ，かつ $E_2$ に含まれる。

・・・ス

・$\cfrac{3}{5}<t<1$ のとき

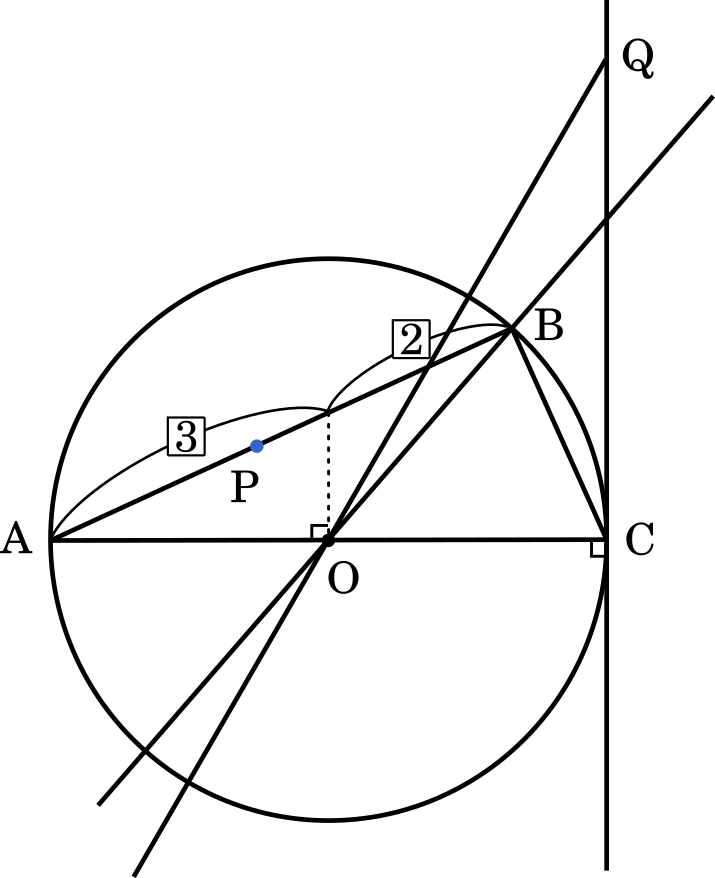
点 Q は $D_1$ に含まれ，かつ $E_1$ に含まれる。

・・・セ

(3)

$\overrightarrow{\text{OQ}}=(k-kt)\overrightarrow{\text{OA}}+kt\overrightarrow{\text{OB}}$ ・・・①
$k=\cfrac{3}{5t-3}$ ・・・②

$t=\cfrac{1}{2}$ のとき，①より

$\overrightarrow{\text{OQ}}=k(1-t)\overrightarrow{\text{OA}}+kt\overrightarrow{\text{OB}}$
$=\cfrac{1}{2}k\overrightarrow{\text{OA}}+\cfrac{1}{2}k\overrightarrow{\text{OB}}$
$=\cfrac{1}{2}k(\overrightarrow{\text{OA}}+\overrightarrow{\text{OB}})$
$|\overrightarrow{\text{OQ}}|^2=\cfrac{1}{4}k^2(\overrightarrow{\text{OA}}+\overrightarrow{\text{OB}})^2$
$=\cfrac{1}{4}k^2(|\overrightarrow{\text{OA}}|^2+2\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}+|\overrightarrow{\text{OB}}|^2)$
$=\cfrac{1}{4}k^2\Big(1-\cfrac{4}{3}+1\Big)$
$=\cfrac{1}{4}k^2\cdot\cfrac{2}{3}$
$=\cfrac{1}{6}k^2$

ここで，$k$ の式に $t=\cfrac{1}{2}$ を代入すると

$k=\cfrac{3}{5t-3}$
$=\cfrac{3}{\cfrac{5}{2}-3}$
$=\cfrac{3\times2}{\Big(\cfrac{5}{2}-3\Big)\times2}$
$=\cfrac{6}{5-6}$
$=-6$

となるので

$k^2=(-6)^2=6$

よって

$|\overrightarrow{\text{OQ}}|^2=\cfrac{1}{6}(-6)^2=6$
$|\overrightarrow{\text{OQ}}|=\sqrt{6}$

・・・ソ

直線 OA に関して，$t=\cfrac{1}{2}$ のときの点 Q と対称な点を R とすると

$\overrightarrow{\text{CR}}=-\overrightarrow{\text{CQ}}$

・・・タ

$=-(k-kt+1)\overrightarrow{\text{OA}}-kt\overrightarrow{\text{OB}}$
$=(kt-k-1)\overrightarrow{\text{OA}}-kt\overrightarrow{\text{OB}}$

$t=\cfrac{1}{2}$，$k=-6$ を代入して

$=\Big\{(-6)\cdot\cfrac{1}{2}-(-6)-1\Big\}\overrightarrow{\text{OA}}-(-6)\cdot\cfrac{1}{2}\overrightarrow{\text{OB}}$
$=2\overrightarrow{\text{OA}}+3\overrightarrow{\text{OB}}$

・・・チ,ツ

$t=\cfrac{1}{2}$ のときの点 P，Q の位置関係は以下のようになる。このとき $\text{OQ}=\text{OR}=\sqrt{6}$ である。

また，$t\not=\cfrac{1}{2}$ のとき，$\text{OQ}=\text{OR}=\sqrt{6}$ となる点 P のおきかたはもう一通りある。

このとき，$t=\cfrac{1}{2}$ のときの $\overrightarrow{\text{CR}}$ と，$t\not=\cfrac{1}{2}$ のときの $\overrightarrow{\text{CQ’}}$ は同一のベクトルである。

$\overrightarrow{\text{CQ’}}=(k-kt+1)\overrightarrow{\text{OA}}+kt\overrightarrow{\text{OB}}$ として

$\overrightarrow{\text{CR}}=2\overrightarrow{\text{OA}}+3\overrightarrow{\text{OB}}$

と比べると

$\begin{cases}k-kt+1=2\cdots(\text{A})\\kt=3\cdots(\text{B})\end{cases}$

が成り立つ。

(A)+(B)

$k+1=5$
$k=4$

(B) に代入して

$4t=3$
$t=\cfrac{3}{4}$

・・・テ,ト

問題文

第５問（第３問～第５問は，いずれか２問を選択し，解答しなさい。）

平面上の点 O を中心とする半径 1 の円周上に，3 点 A，B，C があり，$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=-\cfrac{2}{3}$ および $\overrightarrow{\text{OC}}=-\overrightarrow{\text{OA}}$ を満たすとする。$t$ を $0<t<1$ を満たす実数とし，線分 AB を $t:(1-t)$ に内分する点を P とする。また，直線 OP 上に点 Q をとる。

(1) $\cos\angle\text{AOB}=\cfrac{\boxed{\enspace\textsf{アイ}\enspace}}{\boxed{\enspace\textsf{ウ}\enspace}}$ である。

また，実数 $k$ を用いて，$\overrightarrow{\text{OQ}}=k\overrightarrow{\text{OP}}$ と表せる。したがって

$\overrightarrow{\text{OQ}}=\boxed{\boxed{\enspace\textsf{エ}\enspace}}\space\overrightarrow{\text{OA}}+\boxed{\boxed{\enspace\textsf{オ}\enspace}}\space\overrightarrow{\text{OB}}$ ・・・①
$\overrightarrow{\text{CQ}}=\boxed{\boxed{\enspace\textsf{カ}\enspace}}\space\overrightarrow{\text{OA}}+\boxed{\boxed{\enspace\textsf{キ}\enspace}}\space\overrightarrow{\text{OB}}$

となる。

$\overrightarrow{\text{OA}}$ と $\overrightarrow{\text{OP}}$ が垂直となるのは，$t=\cfrac{\boxed{\enspace\textsf{ク}\enspace}}{\boxed{\enspace\textsf{ケ}\enspace}}$ のときである。

$\boxed{\boxed{\enspace\text{エ}\enspace}}$～$\boxed{\boxed{\enspace\text{キ}\enspace}}$ の解答群(同じものを繰り返し選んでもよい｡)

以下，$t\not=\cfrac{\boxed{\enspace\text{ク}\enspace}}{\boxed{\enspace\text{ケ}\enspace}}$

とし，∠OCQ が直角であるとする。

(2) ∠OCQ が直角であることにより，(1)の $k$ は
$k=\cfrac{\boxed{\enspace\textsf{コ}\enspace}}{\boxed{\enspace\textsf{サ}\enspace}\space t-\boxed{\enspace\textsf{シ}\enspace}}$ ・・・②

となることがわかる。

平面から直線 OA を除いた部分は，直線 OA を境に二つの部分に分けられる。そのうち，点 B を含む部分を $D_1$，含まない部分を $D_2$ とする。また，平面から直線 OB を除いた部分は，直線 OB を境に二つの部分に分けられる。そのうち，点 A を含む部分を $E_1$，含まない部分を $E_2$ とする。

・$0<t<\cfrac{\boxed{\enspace\text{ク}\enspace}}{\boxed{\enspace\text{ケ}\enspace}}$ ならば点 Q は $\boxed{\boxed{\enspace\textsf{ス}\enspace}}$。
・$\cfrac{\boxed{\enspace\text{ク}\enspace}}{\boxed{\enspace\text{ケ}\enspace}}<t<1$ ならば，点 Q は $\boxed{\boxed{\enspace\textsf{セ}\enspace}}$。

$\boxed{\boxed{\enspace\text{ス}\enspace}}$～$\boxed{\boxed{\enspace\text{セ}\enspace}}$ の解答群(同じものを繰り返し選んでもよい｡)

(3) 太郎さんと花子さんは，点 P の位置と $|\overrightarrow{\text{OQ}}|$ の関係について考えている。

$t=\cfrac{1}{2}$ のとき，①と②により，$|\overrightarrow{\text{OQ}}|=\sqrt{\boxed{\enspace\textsf{ソ}\enspace}}$ とわかる。

直線 OA に関して，$t=\cfrac{1}{2}$ のときの点 Qと対称な点を R とすると

$\overrightarrow{\text{CR}}=\boxed{\enspace\textsf{タ}\enspace}\space\overrightarrow{\text{CQ}}$
$=\boxed{\enspace\textsf{チ}\enspace}\space\overrightarrow{\text{OA}}+\boxed{\enspace\textsf{チ}\enspace}\space\overrightarrow{\text{OB}}$

となる。

$t\not=\cfrac{1}{2}$ のとき，$|\overrightarrow{\text{OQ}}|=\sqrt{\boxed{\enspace\text{ソ}\enspace}}$  となる $t$ の値は $\cfrac{\boxed{\enspace\textsf{テ}\enspace}}{\boxed{\enspace\textsf{ト}\enspace}}$ である。