【スマホで読む・わかりやすい】共通テスト数学IIB2022本試【解説・正解・問題】

第３問　正解

アイ 25　ウエオ 100　カ 2
キ 2　ク 1　ケ,コ 4,2
サ 3　シス 11　セ 2

(1)

ジャガイモ 400 個のうち 200 g を超えるものが 25 % 含まれていることから，$Z$ は二項分布

$B(400,0.25)$

に従う。

・・・アイ

また，$Z$ の平均（期待値）は

確率変数 $Z$ が二項分布 $B(n,p)$ に従うとき

$E(Z)=np$

で求められる。これを用いて

$E(Z)=400\cdot0.25$
$=100$

・・・ウエオ

これは，ジャガイモ 400 個のうち，重さ 200 g を超えるものが 100 個あることが期待できるということである。

(2)

確率変数 $Z$ の期待値を $m$ とし，$Z$ を $z_1,z_2,z_3,\cdots,z_n$，それぞれの事象が起こる確率を $p_1,p_2,p_3,\cdots$ とすると，その分散は

$V(Z)=(z_1-m)^2p_1+(z_2-m)^2+(z_3-m)^3+\cdots+(z_n-m)^2p_n$

で与えられる。これを $R=\cfrac{Z}{400}$ とすると

$V(R)=\Big(\cfrac{z_1}{400}-\cfrac{m}{400}\Big)^2p_1+\Big(\cfrac{z_2}{400}-\cfrac{m}{400}\Big)^2p_2+\Big(\cfrac{z_3}{400}-\cfrac{m}{400}\Big)^2p_3+\cdots+\Big(\cfrac{z_n}{400}-\cfrac{m}{400}\Big)^2p_n$
$=\cfrac{1}{400^2}\{(z_1-m)^2p_1+(z_2-m)^2+(z_3-m)^3+\cdots+(z_n-m)^2p_n\}$
$=\cfrac{1}{400^2}\cdot V(Z)$

となる。

$Z$ の分散は

$V(Z)=np(1-p)$

で求められる。これを用いて

$V(Z)=400\cdot0.25\cdot(1-0.25)$
$=400\cdot\cfrac{1}{4}\cdot\cfrac{3}{4}$

$=75$

よって，$R$ の標準偏差は

$\sigma(R)=\sqrt{\cfrac{75}{400^2}}$
$=\cfrac{5\sqrt{3}}{400}$
$=\cfrac{\sqrt{3}}{80}$

・・・カ

標本の大きさ 400 は十分に大きいので，$R$ は近似的に正規分布

$N\Big(0.25,\big(\cfrac{\sqrt{3}}{4}\big)^2\Big)$

に従う。

そして，確率変数 $R$ が正規分布 $N(m,\sigma^2)$ に従うとき

$R_0=\cfrac{R-m}{\sigma}$

とおくと，確率変数 $R_0$ は標準正規分布 $N(0,1)$ に従う。よって

$R_0=\cfrac{R-0.25}{\cfrac{\sqrt{3}}{80}}$
$=\cfrac{80R-20}{\sqrt{3}}$

これより

$P(R\geqq x)=0.0465$ は

$P\Big(R_0\geqq\cfrac{80R-20}{\sqrt{3}}\Big)=0.0465$

と書き換えることができる。

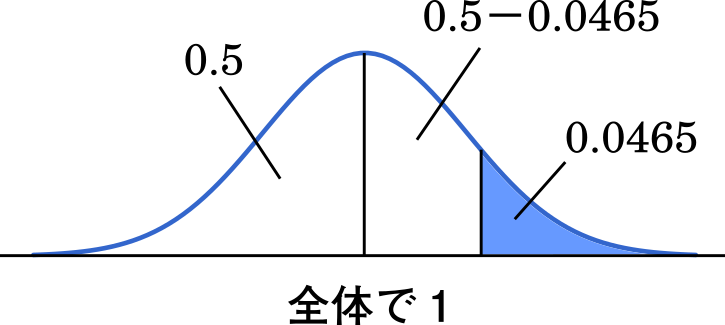
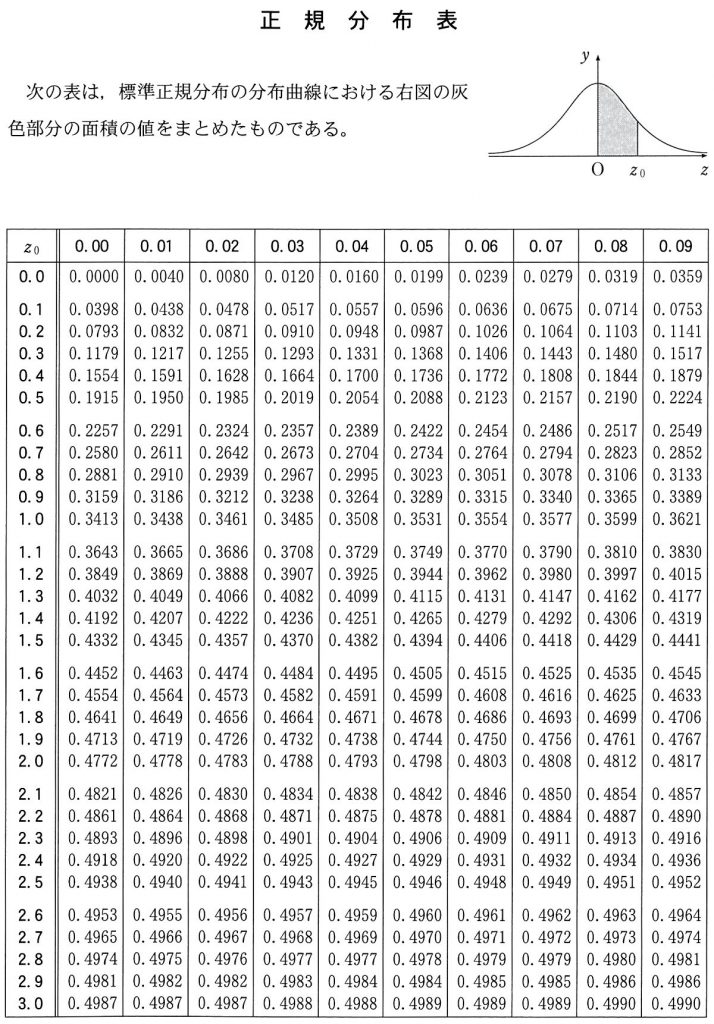
標準正規分布表を用いて，上の図の青色の部分を求めるには $0.5$ から $0.0465$ を引けば良い。

$0.5-0.0465=0.4535$

正規分布表より

$x_0=1.68$

よって

$\cfrac{80x-20}{\sqrt{3}}=1.68$

$80x-20=1.68\cdot1.73$
$80x-20=2.9064$
$80x=22.9064$
$x=0.28633$

よって，② 0.286 が最も適当である。

・・・キ

(3)

$X$ の取りうる値 $x$ の範囲は $100\leqq x\leqq300$ だから，$P(100\leqq X\leqq300)$ は全事象を表す。したがって

$P(100\leqq x\leqq300)=1$

・・・ク

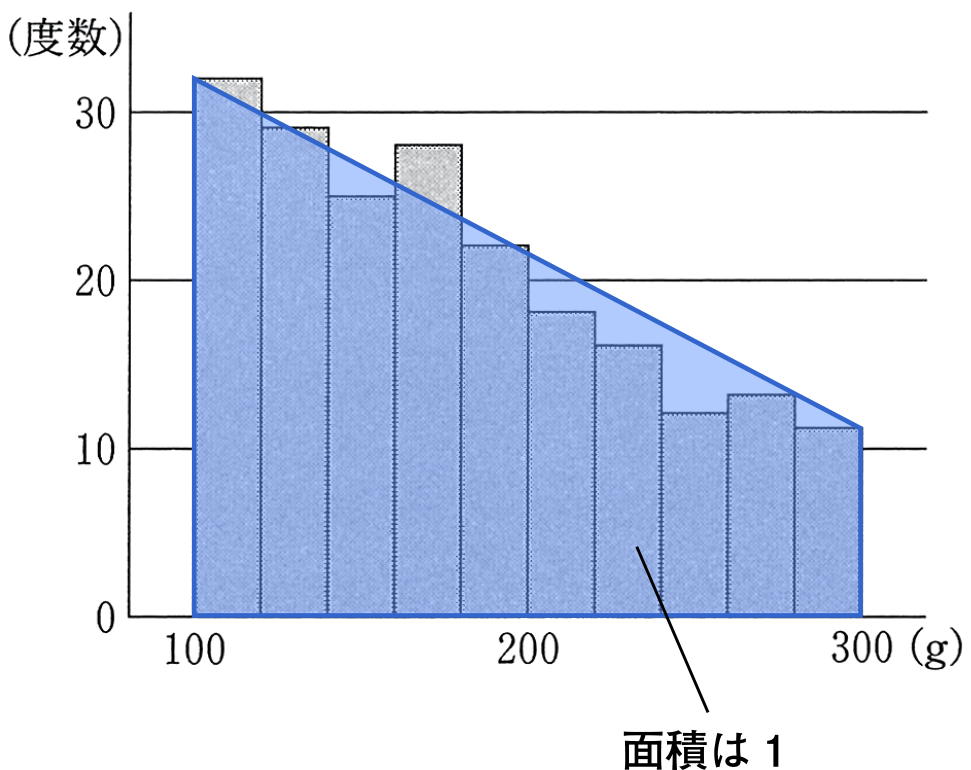
上のグラフの縦軸を度数ではなく確率として捉えると，台形の面積は 1 になる。

よって，台形の面積の公式より

$\cfrac{1}{2}\{f(100)+f(300)\}\cdot(300-100)=1$

$f(x)=ax+b$ より

$\cfrac{1}{2}(100a+b+300a+b)\cdot200=1$
$100(400a+2b)=1$
$4\cdot10^4a+2\cdot10^2b=1$　・・・①

・・・ケ,コ

また

$m=\cfrac{26}{3}\cdot10^6a+4\cdot10^4b=180$ ・・・②

より，①と②を連立して，$f(x)$ を求めると良い。

①×200－②

$\begin{aligned}8\cdot10^6a+4\cdot10^4b=200\\-)\cfrac{26}{3}\cdot10^6a+4\cdot10^4b=180\\\hline-\cfrac{2}{3}\cdot10^6a=20\end{aligned}$
$10^6a=-30$
$a=-\cfrac{30}{10^6}=-\cfrac{3}{10^5}$
$=-3\cdot10^{-5}$

①に代入して

$4\cdot10^4(-3\cdot10^{-5})+2\cdot10^2b=1$
$-12\cdot10^{-1}+2\cdot10^2b=1$
$-1.2+2\cdot10^2b=1$
$2\cdot10^2b=2.2$
$b=\cfrac{1.1}{10^2}$
$=1.1\cdot10^{-2}$
$=11\cdot10^{-3}$

したがって

$f(x)=-3\cdot10^{-5}x+11\cdot10^{-3}$

・・・サ,シス

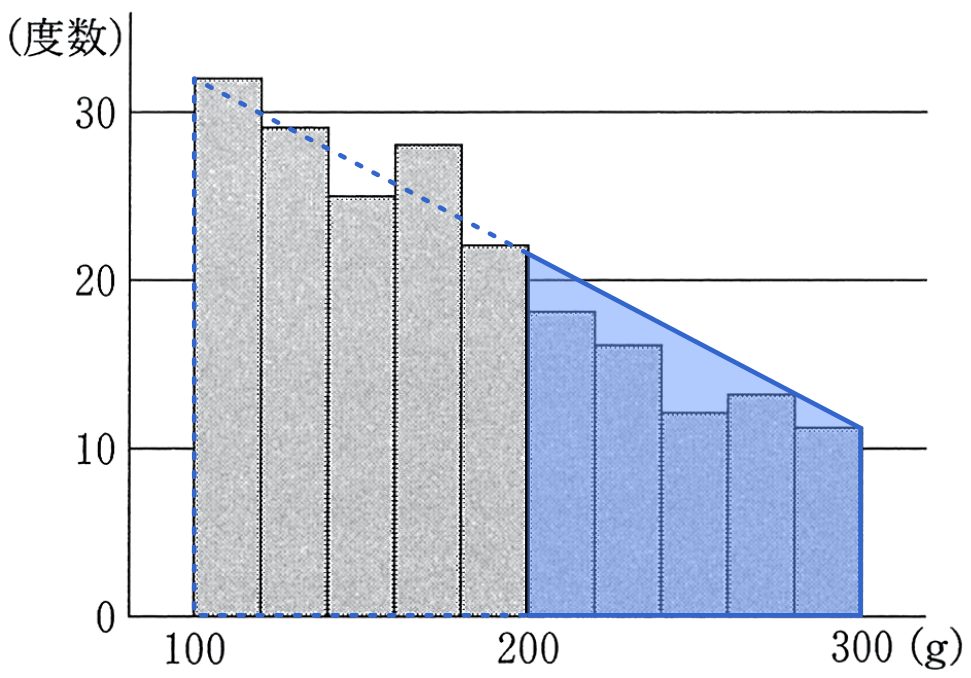
次に，重さが 200 g 以上のものの割合を求めるには，上の図の台形の面積を求めれば良い。

$\cfrac{1}{2}\{f(200)+f(300)\}(300-200)$
$=\cfrac{1}{2}(-3\cdot10^{-5}\cdot200+11\cdot10^{-3}-3\cdot10^{-5}\cdot300+11\cdot10^{-3})\cdot100$
$=50(-6\cdot10^{-3}+11\cdot10^{-3}-9\cdot10^{-3}+11\cdot10^{-3})$
$=50\cdot7\cdot10^{-3}$
$=350\cdot10^{-3}$
$=0.35$

したがって，求める割合は

35 %

・・・セ

問題文

第３問（第３問～第５問は，いずれか２問を選択し，解答しなさい。）

以下の問題を解答するにあたっては，必要に応じて41ページの正規分布表を用いてもよい。

ジャガイモを栽培し販売している会社に勤務する花子さんは，A 地区と B 地区で収穫されるジャガイモについて調べることになった。

(1) A 地区で収穫されるジャガイモには 1 の重さが 200 g を超えるものが 25 ％ 含まれることが経験的にわかっている。花子さんは A 地区で収穫されたジャガイモから 400 個を無作為に抽出し，重さを計測した。そのうち，重さが 200 g を超えるジャガイモの個数を表す確率変数を $Z$ とする。このとき $Z$ は二項分布 $B(400,0.\boxed{\enspace\textsf{アイ}\enspace})$ に従うから，$Z$ の平均(期待値)は $\boxed{\enspace\textsf{ウエオ}\enspace}$ である。

(2) $Z$ を(1)の確率変数とし，A 地区で収穫されたジャガイモ 400 個からなる標本において，重さが 200 g を超えていたジャガイモの標本における比率を $R=\cfrac{Z}{400}$ とする。このとき，$R$ の標準偏差は $\sigma(R)=\boxed{\boxed{\enspace\textsf{カ}\enspace}}$ である。

標本の大きさ 400 は十分に大きいので，$R$ は近似的に正規分布 $N\Big(0.\boxed{\enspace\text{アイ}\enspace},\big(\boxed{\boxed{\enspace\text{カ}\enspace}}\big)^2\Big)$ に従う。

したがって，$P(R\geqq x)=0.0465$ となるような $x$ の値は $\boxed{\boxed{\enspace\textsf{キ}\enspace}}$ となる。ただし，$\boxed{\boxed{\enspace\text{キ}\enspace}}$ の計算においては $\sqrt{3}=1.73$ とする。

$\boxed{\boxed{\enspace\text{カ}\enspace}}$ の解答群

$\boxed{\boxed{\enspace\text{キ}\enspace}}$ については，最も適当なものを，次の $\textsf{\textcircled{0}}$ ～ ③ のうちから一つ選べ。

(3) B 地区で収穫され，出荷される予定のジャガイモ 1 個の重さは 100 g から 300 g の間に分布している。B 地区で収穫され，出荷される予定のジャガイモ 1 個の重さを表す確率変数を $X$ とするとき，$X$ は連続型確率変数であり，$X$ のとり得る値 $x$ の範囲は $100\leqq x\leqq300$ である。

花子さんは，B 地区で収穫され，出荷される予定のすべてのジャガイモのうち，重さが 200 g 以上のものの割合を見積もりたいと考えた。そのために花子さんは，$X$ の確率密度関数 $f(x)$ として適当な関数を定め，それを用いて割合を見積もるという方針を立てた。

B 地区で収穫され，出荷される予定のジャガイモから 206 個を無作為に抽出したところ，重さの標本平均は 180 g であった。図 1 はこの標本のヒストグラムである。

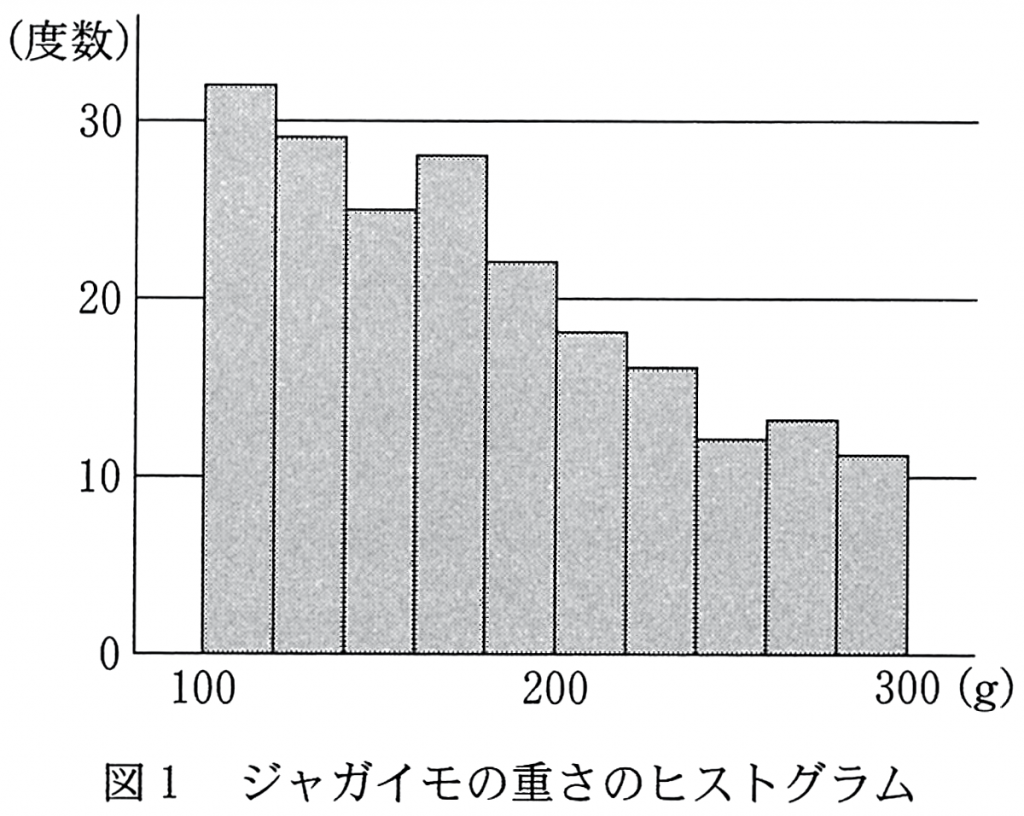
花子さんは図 1 のヒストグラムにおいて，重さ $x$ の増加とともに度数がほぼ一定の割合で減少している傾向に着目し，$X$ の確率密度関数 $f(x)$ として，1 次関数

$f(x)=ax+b$ $(100\leqq x\leqq300)$

を考えることにした。ただし，$100\leqq x\leqq300$ の範囲で $f(x)\geqq0$ とする。

このとき，$P(100\leqq X\leqq300)=\boxed{\enspace\textsf{ク}\enspace}$ であることから

$\boxed{\enspace\textsf{ケ}\enspace}\cdot10^4a+\boxed{\enspace\textsf{コ}\enspace}\cdot10^2b=\boxed{\enspace\text{ク}\enspace}$ ・・・①

である。

花子さんは，$X$ の平均(期待値)が重さの標本平均 180 g と等しくなるように確率密度関数を定める方法を用いることにした。

連続型確率変数 $X$ のとり得る値 $X$ の範囲が $100\leqq x\leqq 300$ で，その確率密度関数が $f(x)$ とき，$X$ の平均(期待値) $m$ は

$\displaystyle m=\int_{100}^{300}xf(x)dx$

で定義される。この定義と花子さんの採用した方法から

$m=\cfrac{26}{3}\cdot10^6a+4\cdot10^4b=180$ ・・・②

となる。①と②により，確率密度関数は

$f(x)=-\boxed{\enspace\textsf{サ}\enspace}\cdot10^{-5}x+\boxed{\enspace\textsf{シス}\enspace}\cdot10^{-3}・・・③$

と得られる。このようにして得られた③の $f(x)$ は，$100\leqq x\leqq300$ の範囲で $f(x)\geqq0$ を満たしており，確かに確率密度関数として適当である。

したがって，この花子さんの方針に基づくと，B 地区で収穫され，出荷される予定のすべてのジャガイモのうち，重さが 200 g 以上のものは $\boxed{\boxed{\enspace\textsf{セ}\enspace}}$ % あると見積もることができる。

$\boxed{\boxed{\enspace\text{セ}\enspace}}$ については，最も適当なものを，次の $\textsf{\textcircled{0}}$ ～ ③ のうちから一つ選べ。