【スマホで読む・わかりやすい】共通テスト数学IA2022本試【解説・正解・問題】

第５問　正解

ア,イ 1, 2　ウ,エ,オ 2, 1, 3
カ,キ,ク 2, 2, 3　ケ 4
コ,サ　3, 2　シス,セ 13, 6
ソタ,チ 13, 4　ツテ,トナ 44, 15
ニ,ヌ　1, 3

(1)

点 G は △ABC の重心だから，AG : EG = 2 : 1 である。

また，点 D は AG の中点だから

AD : DG : EG = 1 : 1 : 1

である。

したがって，AD : DE = 1 : 2 となるので

$\cfrac{\text{AD}}{\text{DE}}=\cfrac{1}{2}$

・・・アイ

次に，メネラウスの定理を用いて

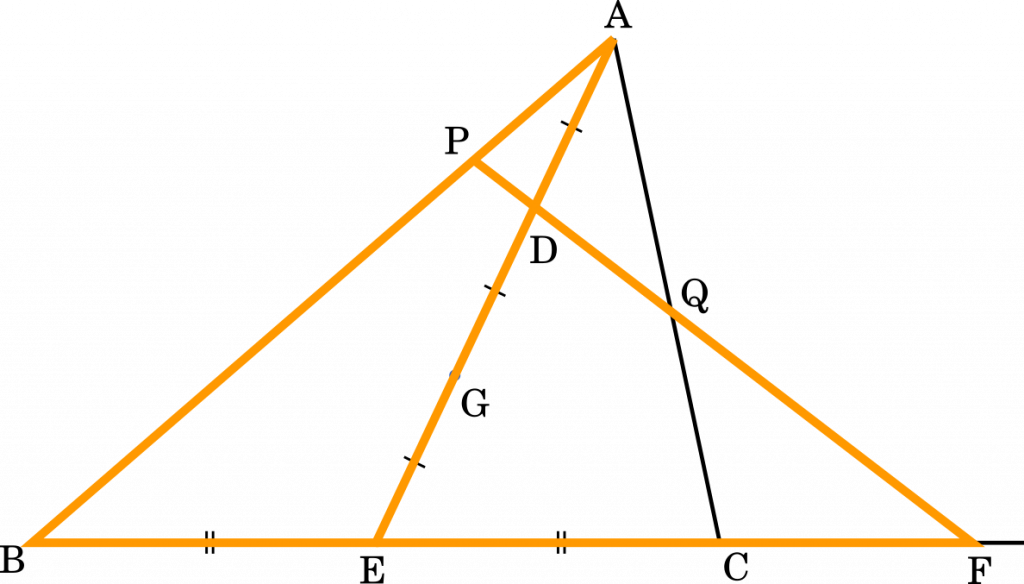
$\cfrac{\text{AP}}{\text{PB}}\times\cfrac{\text{BF}}{\text{FE}}\times\cfrac{\text{ED}}{\text{DA}}=1$
$\cfrac{\text{PA}}{\text{BP}}\times\cfrac{\text{BF}}{\text{EF}}\times\cfrac{\text{2}}{\text{1}}=1$
$\cfrac{\text{BP}}{\text{PA}}=2\times\cfrac{\text{BF}}{\text{EF}}$

・・・ウ,エ,オ

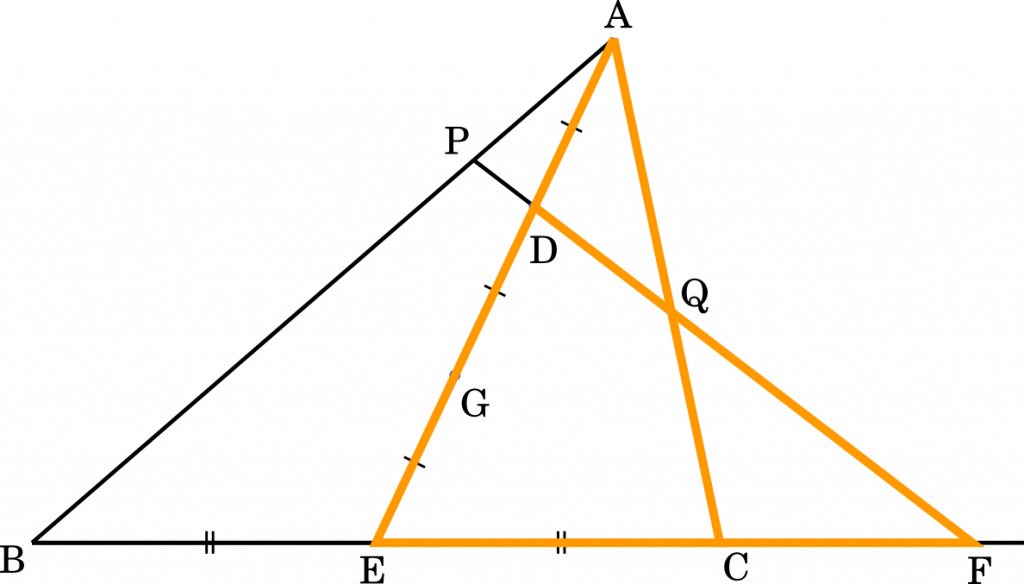
$\cfrac{\text{AD}}{\text{DE}}\times\cfrac{\text{EF}}{\text{FC}}\times\cfrac{\text{CQ}}{\text{QA}}=1$

$\cfrac{1}{2}\times\cfrac{\text{EF}}{\text{CF}}\times\cfrac{\text{CQ}}{\text{AQ}}=1$

$\cfrac{\text{CQ}}{\text{AQ}}=2\times\cfrac{\text{CF}}{\text{EF}}$

・・・カ,キ,ク

よって

$\cfrac{\text{BP}}{\text{AP}}+\cfrac{\text{CQ}}{\text{AQ}}=2\times\cfrac{\text{BF}+\text{CF}}{\text{EF}}$ ・・・①

ここで

$\text{CF}=\text{BF}-\text{BC}$ ・・・②

また，点 E は辺 BC の中点であることより

$\text{EF}=\cfrac{\text{BC}}{2}+\text{CF}$
$=\cfrac{\text{BC}}{2}+\text{BF}-\text{BC}$
$=\cfrac{\text{BC}+2\text{BF}-2\text{BC}}{2}$
$=\cfrac{2\text{BF}-\text{BC}}{2}$ ・・・③

②，③を①に代入すると

$\cfrac{\text{BP}}{\text{AP}}+\cfrac{\text{CQ}}{\text{AQ}}=2\times\cfrac{2\text{BF}-\text{BC}}{\cfrac{2\text{BF}-\text{BC}}{2}}$
$=2\times\cfrac{\enspace1\enspace}{\cfrac{1}{2}}$

$=2\times\cfrac{\enspace1\times2\enspace}{\cfrac{1}{2}\times2}$
$=2\times2$
$=4$

・・・ケ

(2)

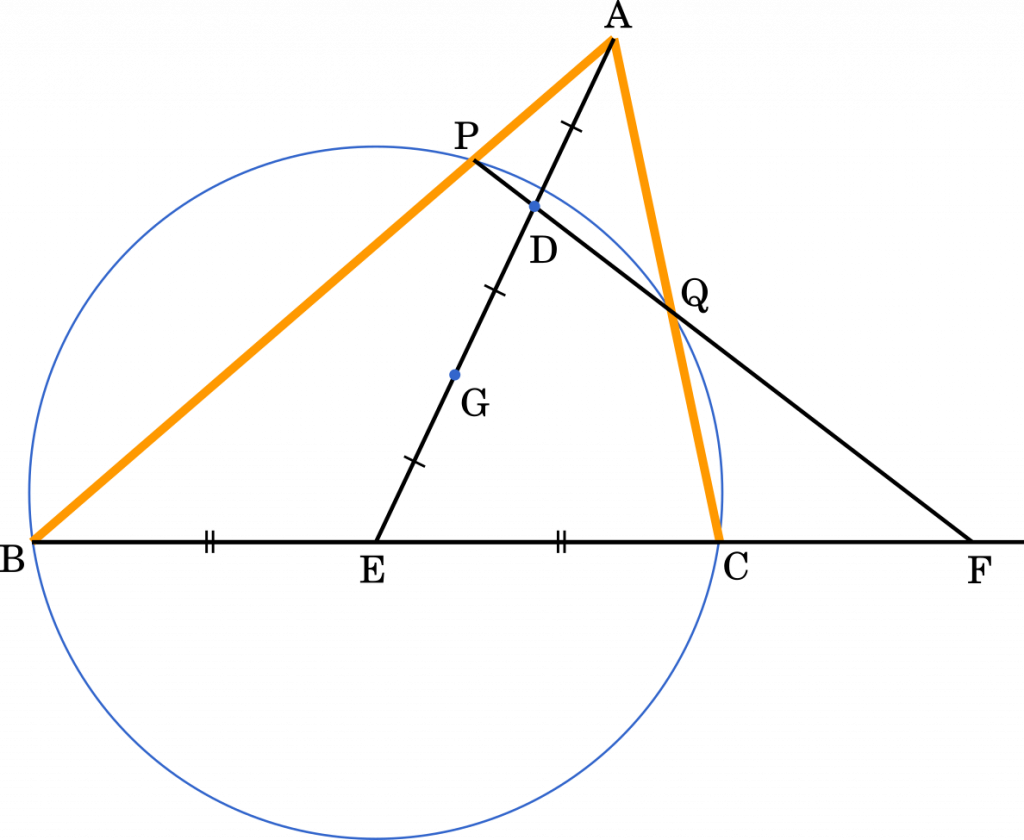
方べきの定理より

$\text{AP}\cdot\text{AB}=\text{AQ}\cdot\text{AC}$
$9\text{AP}=6\text{AQ}$
$\text{AQ}=\cfrac{3}{2}\text{AP}$

・・・コサ

次に，AP を求める。

(2)で求めた

$\cfrac{\text{BP}}{\text{AP}}+\cfrac{\text{CQ}}{\text{AQ}}=4$

を利用する。考え方としては，BP，CQ，AQ を AP に合わせていくと良い。

$\cfrac{\text{BP}}{\text{AP}}+\cfrac{\text{CQ}}{\cfrac{3}{2}\text{AP}}=4$
$\cfrac{\text{BP}}{\text{AP}}+\cfrac{\text{CQ}\times2}{\cfrac{3}{2}\text{AP}\times2}=4$
$\cfrac{\text{BP}}{\text{AP}}+\cfrac{2\text{CQ}}{3\text{AP}}=4$
$\cfrac{3\text{BP}+2\text{CQ}}{3\text{AP}}=4$
$3\text{BP}+2\text{CQ}=12\text{AP}$

ここで

$\text{BP}=\text{AB}-\text{AP}$
$=9-\text{AP}$
$\text{CQ}=\text{AC}-\text{AQ}$
$=6-\cfrac{3}{2}\text{AP}$

だから

$3(9-\text{AP})+2\Big(6-\cfrac{3}{2}\text{AP}\Big)=12\text{AP}$
$27-3\text{AP}+12-3\text{AP}=12\text{AP}$
$18\text{AP}=39$
$\text{AP}=\cfrac{39}{18}=\cfrac{13}{6}$

・・・シス，セ

さらに AQ を求めると

$\text{AQ}=\cfrac{3}{2}\text{AP}$

より

$\text{AQ}=\cfrac{3}{2}\times\cfrac{13}{6}=\cfrac{4}{13}$

・・・ソタ，チ

(3)

(1)で求めた，メネラウスの定理を用いた 2 つの式から

$\cfrac{\text{BP}}{\text{AP}}+\cfrac{\text{CQ}}{\text{AQ}}$

の形に変形していくと良い。

まず

$\cfrac{\text{AP}}{\text{BP}}\times\cfrac{\text{BF}}{\text{EF}}\times\cfrac{\text{ED}}{\text{AD}}=1$

より

$\cfrac{\text{BP}}{\text{AP}}=\cfrac{\text{BF}}{\text{EF}}\times\cfrac{\text{ED}}{\text{AD}}$ ・・・④

また，もう 1 つの式から

$\cfrac{\text{AD}}{\text{ED}}\times\cfrac{\text{EF}}{\text{CF}}\times\cfrac{\text{CQ}}{\text{AQ}}=1$

$\cfrac{\text{CQ}}{\text{AQ}}=\cfrac{\text{ED}}{\text{AD}}\times\cfrac{\text{CF}}{\text{EF}}$ ・・・⑤

④，⑤より

$\cfrac{\text{BP}}{\text{AP}}+\cfrac{\text{CQ}}{\text{AQ}}$
$=\cfrac{\text{BF}}{\text{EF}}\times\cfrac{\text{ED}}{\text{AD}}+\cfrac{\text{ED}}{\text{AD}}\times\cfrac{\text{CF}}{\text{EF}}$
$=\cfrac{\text{ED}}{\text{AD}}\times\cfrac{\text{BF}+\text{CF}}{\text{EF}}$

ここで，(2)で求めた

$\text{CF}=\text{BF}-\text{BC}$ ・・・②

$\text{EF}=\cfrac{2\text{BF}-\text{BC}}{2}$ ・・・③

を代入すると

$=\cfrac{\text{ED}}{\text{AD}}\times\cfrac{2\text{BF}-\text{BC}}{\cfrac{2\text{BF}-\text{BC}}{2}}$
$=\cfrac{\text{ED}}{\text{AD}}\times2$

よって

$\cfrac{\text{ED}}{\text{AD}}\times2=10$

が成り立つから

$\cfrac{\text{ED}}{\text{AD}}=5$

となる。これより

AD : ED = 1 : 5 ・・・⑥

が成り立つ。

また，点 G は △ABC の重心だから

AG : EG = 2 : 1 = 4 : 2 ・・・⑦

である。

したがって

$\cfrac{\text{AD}}{\text{DG}}=\cfrac{1}{3}$

・・・ニ,ヌ

問題文

第５問（第３問～第５問は，いずれか２問を選択し，解答しなさい。）

△ABC の重心を G とし，線分 AG 上で点 A とは異なる位置に点 D をとる。直線 AG と辺 BC の交点を E とする。また，直線 BC 上で辺 BC 上にはない位置に点 F をとる。直線 DF と辺 AB の交点を P，直線 DF と辺AC の交点を Q とする。

(1) 点 D は線分 AG の中点であるとする。このとき，△ABC の形状に関係なく

$\cfrac{\text{AD}}{\text{DE}}=\cfrac{\boxed{\enspace\textsf{ア}\enspace}}{\boxed{\enspace\textsf{イ}\enspace}}$

である。また，点 F の位置に関係なく

$\cfrac{\text{BP}}{\text{AP}}=\boxed{\enspace\textsf{ウ}\enspace}\times\cfrac{\boxed{\boxed{\enspace\textsf{エ}\enspace}}}{\boxed{\boxed{\enspace\textsf{オ}\enspace}}}$

$\cfrac{\text{CQ}}{\text{AQ}}=\boxed{\enspace\textsf{カ}\enspace}\times\cfrac{\boxed{\boxed{\enspace\textsf{キ}\enspace}}}{\boxed{\boxed{\enspace\textsf{ク}\enspace}}}$

であるので，つねに

$\cfrac{\text{BP}}{\text{AP}}+\cfrac{\text{CQ}}{\text{AQ}}=\boxed{\enspace\textsf{ケ}\enspace}$

となる。

$\boxed{\boxed{\enspace\text{エ}\enspace}}$，$\boxed{\boxed{\enspace\text{オ}\enspace}}$，$\boxed{\boxed{\enspace\text{キ}\enspace}}$，$\boxed{\boxed{\enspace\text{ク}\enspace}}$ の解答群(同じものを繰り返し選んでもよい。）

(2) AB = 9，RC = 8，AC = 6 とし，(1)と同様に点 D は線分 AG の中点であるとする。ここで，4 点 B，C，Q，P が同一円周上にあるように点 F をとる。

このとき，$\text{AQ}=\cfrac{\boxed{\enspace\textsf{コ}\enspace}}{\boxed{\enspace\textsf{サ}\enspace}}$ であるから

$\text{AP}=\cfrac{\boxed{\enspace\textsf{シス}\enspace}}{\boxed{\enspace\textsf{セ}\enspace}}$

$\text{AQ}=\cfrac{\boxed{\enspace\textsf{ソタ}\enspace}}{\boxed{\enspace\textsf{チ}\enspace}}$

であり

$\text{CF}=\cfrac{\boxed{\enspace\textsf{ツテ}\enspace}}{\boxed{\enspace\textsf{トナ}\enspace}}$

である。

(3) △ABC の形状や点 F の位置に関係なく，つねに $\cfrac{\text{BP}}{\text{AP}}+\cfrac{\text{CQ}}{\text{AQ}}=10$ となるのは，$\cfrac{\text{AD}}{\text{DG}}=\cfrac{\boxed{\enspace\textsf{ニ}\enspace}}{\boxed{\enspace\textsf{ヌ}\enspace}}$ のときである。