【スマホで読む・わかりやすい】共通テスト数学IA2022本試【解説・正解・問題】

第２問　正解

ア 3　イ 2　ウ 5　エ 9　オ 6
カ 1　キ,ク 3, 1　ケ,コ,サ 2, 2, 0
シ,ス 0,3　セ 2　ソ.タチ 0.63　ツ 3

第２問〔１〕(1)

$p=4$，$q=-4$ を①に代入すると

$x^2+4x-4=0$
$x=-2\pm\sqrt{2^2-1\times(-4)}$
$=-2\pm2\sqrt{2}$

①を満たす実数 $x$ の個数は 2 個。

次に $p=4$，$q=-4$ を②に代入すると

$x^2-4x+4=0$
$(x-2)^2=0$
$x=2$

したがって，$p=4$，$q=-4$ のとき，$n=3$ である。

・・・ア

また，$p=1$，$q=-2$ を①に代入すると

$x^2+x-2=0$
$x=\cfrac{-1\pm\sqrt{1^2-4\times(-2)}}{2}$
$=\cfrac{-1\pm3}{2}$
$=-\cfrac{4}{2},\cfrac{2}{2}$
$=-2,1$

次に，$p=1$，$q=-2$ を②に代入すると

$x^2-2x+1=0$
$(x-1)^2=0$
$x=1$

解が重複することに注意して

$p=1$，$q=-2$ のとき，$n=2$ である。

・・・イ

〔１〕(2)

$p=-6$ のとき①，②は

$x^2-6x+q=0$
$x^2+qx-6=0$

となる。$x=\alpha$ とすると

$\alpha^2-6\alpha+q=0$
$\alpha^2+q\alpha-6=0$

として，式どうしを引くと

$-(6+q)\alpha+q+6=0$
$(6+q)\alpha=q+6$

両辺を $6+q$ で割ると

$\alpha=1$

$\alpha^2-6\alpha+q=0$ に代入すると

$1^2-6\times1+q=0$
$-5+q=0$
$q=5$

$\alpha=1$ は 2 次方程式の解の 1 つである。2 次方程式は重解の場合を除くと解を 2 つ持つので，ここからもう一つの解を求めるとよい。

$q=5$ を $\alpha^2-6\alpha+q=0$ に代入すると

$\alpha^2-6\alpha+5=0$
$(\alpha-1)(\alpha-5)=0$
$\alpha=1,5$

次に $q=5$ を $\alpha^2+q\alpha-6=0$ に代入すると

$\alpha^2+5\alpha-6=0$

$(\alpha+6)(\alpha-1)=0$
$\alpha=-6,1$

よって，$n=3$ である。

さらに，$n=3$ となる他の $q$ の値を求める。

$x^2-6x+q=0$
$x=3\pm\sqrt{3^2-q}$
$=3\pm\sqrt{9-q}$

ここで $q=9$ とすると，$x=3$ となる（重解）。

そして，$x^2+qx-6=0$ の解が $x=3$ でない，2 つの異なる実数解をもてば $n=3$ となる。

$x^2+9x-6=0$ とすると

$x=\cfrac{-9\pm\sqrt{9^2-4\times(-6)}}{2}$
$=\cfrac{-9\pm\sqrt{81+24}}{2}$
$=\cfrac{-9\pm\sqrt{105}}{2}$

よって，$n=3$ となる。

したがって，$n=3$ となる $q$ の値は

$q=5,9$

・・・ウ,エ

〔１〕(3)

$y=x^2-6x+q$　・・・③

平方完成して

$y=(x-3)^2-9+q$

頂点は $(3,\space q-9)$ であり，$q$ の値が変化してもグラフは $x$ 軸方向には移動しない。一方で $q$ の値が増加すると，$y$ 軸に平行に上方向に移動する。

よって，⑥が正しい。

・・・オ

次に

$y=x^2+qx-6$　・・・④

平方完成して

$y=\Big(x+\cfrac{q}{2}\Big)^2-\cfrac{q}{4}-6$

頂点は $\Big(-\cfrac{q}{2},\space-\cfrac{q}{4}-6\Big)$ であり，$q$ が増加すると，$x$ 軸に平行に左方向に移動し，$y$ 軸に平行に下方向に移動する。

したがって，①が正しい。

・・・カ

〔１〕(4)

$5<q<9$ とする。

集合 $A$ について，$x^2-6x+q<0$ の範囲を求める。

$x^2-6x+q=0$ とすると

$x=3\pm\sqrt{9-q}$

となるので

$3-\sqrt{9-q}<x<3+\sqrt{9-q}$

ここで，$q=5$ を $3+\sqrt{9-q}$ に代入すると

$3+\sqrt{9-5}=3+2=5$

$q=9$ を代入すると

$3+\sqrt{9-9}=3$

となる。よって集合 $A$ の最大は 3 より大きく 5 未満である。

同様にして，$3-\sqrt{9-q}$ は

$3-2=1$
$3-0=3$

よって集合 $A$ の最小は 1 より大きく 3 未満である。

また，集合 $B$ について $x^2+qx-6<0$ の範囲を求める。

$x^2+qx-6=0$ とすると

$x=\cfrac{-q\pm\sqrt{q^2+24}}{2}$

となるので

$\cfrac{-q-\sqrt{q^2+24}}{2}<x<\cfrac{-q+\sqrt{q^2+24}}{2}$

ここで，$q=5$ を $\cfrac{-q+\sqrt{q^2+24}}{2}$ に代入すると

$\cfrac{-5+\sqrt{25+24}}{2}$
$=\cfrac{-5+7}{2}$
$=1$

$q=9$ を代入すると

$\cfrac{-9+\sqrt{81+24}}{2}$
$=\cfrac{-9+\sqrt{105}}{2}$

$\sqrt{105}$ の範囲を求めると

$\sqrt{100}<\sqrt{105}<\sqrt{121}$
$10<\sqrt{105}<11$

だから

$1<-9+\sqrt{105}<2$
$\cfrac{1}{2}<\cfrac{-9+\sqrt{105}}{2}<1$

よって集合 $B$ の最大は $\cfrac{1}{2}$ より大きく，1 未満である。

したがって，$x\in A$ は $x\in B$ であるための③必要条件でも十分条件でもない。

・・・キ

次に，$\overline{A}$ の範囲は

$x<3-\sqrt{9-q}$，$x>3+\sqrt{9-q}$

となる。

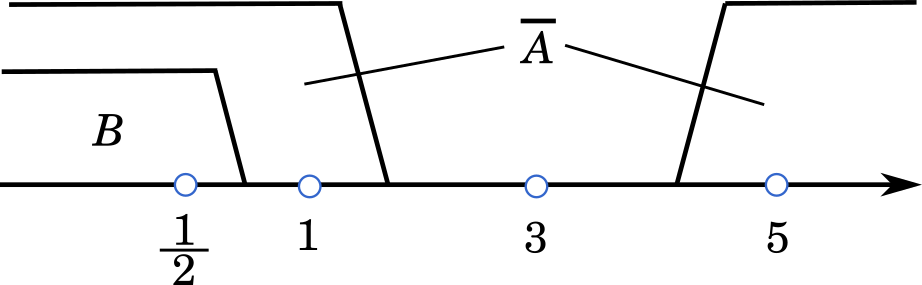
したがって，$x\in B$ のとき $x\in\overline{A}$ が成り立ち，$x\in\overline{A}$ のとき $x\in B$ は成り立たない場合がある。

したがって，$x\in B$ は，$x\in\overline{A}$ であるための①十分条件であるが必要条件ではない。

・・・ク

〔２〕(1)

29 か国の中央値は小さい方から数えて 15 番目の国である。

$\underbrace{\textsf{○○}\cdots\textsf{○}}_{\textsf{0～14}}\underbrace{\textsf{○}}_{15}\underbrace{\textsf{○○}\cdots\textsf{○}}_{\textsf{16～29}}$

図１より，2009年度の中央値は 30 以上 45 未満に含まれる。また図２より，2018年度の中央値は 30 以上 45 未満に含まれる。

したがって，2009年度と2018年度の中央値が含まれる階級の階級値を比較すると，② 両者は等しい。

・・・ケ

第１四分位数は小さい方から数えて 7 番目と 8 番目を足して 2 で割ったものである。

2009年度の第１四分位数は 15 以上 30 未満に含まれ，2018年度の第１四分位数は 15 以上 30 未満に含まれる。

したがって，2009年度と2018年度の第１四分位数が含まれる階級の階級値を比較すると，② 両者は等しい。

・・・コ

第３四分位数は大きい方から数えて 7 番目と 8 番目を足して 2 で割ったものである。

2009年度の第３四分位数は 60 以上 75 未満に含まれ，2018年度の第３四分位数は 45 以上 60 未満に含まれる。

したがって，2009年度と2018年度の第３四分位数が含まれる階級の階級値を比較すると，$\textsf{\textcircled{0}}$ 2018年度の方が小さい。

・・・サ

範囲は最大値から最小値を引いたものである。

2009年度の範囲は 15 以上 180 未満であり，2018年度の範囲は 0 以上 135 未満である。

したがって，2009年度と2018年度の範囲を比較すると，$ \textsf{\textcircled{0}} $ 2018年度の方が小さい。

・・・シ

四分位範囲は第３四分位数から第１四分位数を引いたものであり，$\text{Q}_3-\text{Q}_1$ で表す。

2009年度の $\text{Q}_1$ は 15 以上 30 未満，$\text{Q}_3$ は 60 以上 75 未満である。よって，四分位範囲は

$60-30<\text{Q}_3-\text{Q}_1<75-15$
$30<\text{Q}_3-\text{Q}_1<60$

また，2018年度の $\text{Q}_1$ は 15 以上 30 未満，$\text{Q}_3$ は 45 以上 60 未満である。よって，四分位範囲は

$45-30<\text{Q}_3-\text{Q}_1<60-15$
$15<\text{Q}_3-\text{Q}_1<45$

つまり，2018年度の四分位範囲は2009年度の四分位範囲を上回る場合がある。

したがって，2009年度と2018年度の四分位範囲を比較すると，③ これら二つのヒストグラムからだけでは両者の大小を判断できない。

〔２〕(2)

箱ひげ図より，教育機関１機関あたりの学習者数の最大値は 450 以上 500 未満である。よって，①は不適。

第１四分位数は 50 以上 100 未満である。よって，③は不適。

第３四分位数は 200 以上 250 未満である。よって $\textsf{\textcircled{0}}$ は不適。

したがって，②が正しい。

・・・セ

〔２〕(3)

よって

$r=\cfrac{735.3}{39.3\times29.9}$
$=0.625\cdots$

$S$ と $T$ の相関係数は $0.64$

・・・ソタチ

〔２〕(4)

相関係数が 0.64 であることから，$S$ と $T$ には正の相関があると言える。よって①または③が考えられる。

また，$S$ と $T$ の平均値より，③が適当である。

・・・ツ

問題文

第２問

$p$，$q$ を実数とする。

花子さんと太郎さんは，次の二つの 2 次方程式について考えている。

$x^2+px+q=0$　・・・①
$x^2+qx+p=0$　・・・②

①または②を満たす実数 $x$ の個数を $n$ とおく。

(1) $p=4$，$q=-4$ のとき，$n=\boxed{\enspace\textsf{ア}\enspace}$ である。
また，$p=1$，$q=-2$ のとき，$n=\boxed{\enspace\textsf{イ}\enspace}$ である。

(2) $p=-6$ のとき，$n=3$ になる場合を考える。

$n=3$ となる $q$ の値は

$q=\boxed{\enspace\textsf{ウ}\enspace}$，$\boxed{\enspace\textsf{エ}\enspace}$

である。ただし，$\boxed{\enspace\text{ウ}\enspace}<\boxed{\enspace\text{エ}\enspace}$ とする。

(3) 花子さんと太郎さんは，グラフ表示ソフトを用いて，①，②の左辺を $y$ とおいた 2 次関数 $y=x^2+px+q$ と $y=x^2+qx+p$ のグラフの動きを考えている。

$p=-6$ に固定したまま，$q$ の値だけど変化させる。

$y=x^2-6x+q$　・・・③
$y=x^2+qx-6$　・・・②

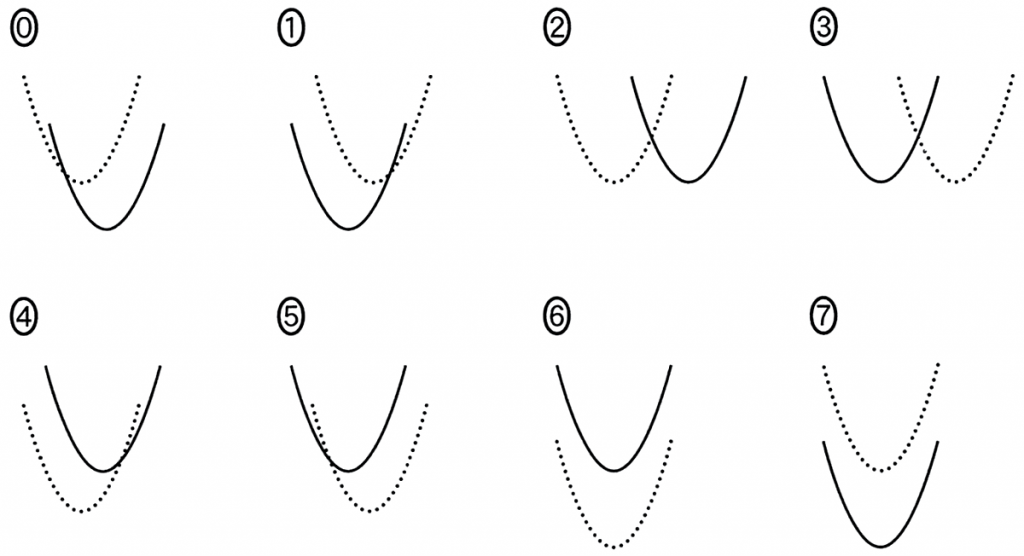
の二つのグラフについて，$q=1$ のときのグラフを点線で，$q$ の値を 1 から増加させたときのグラフを実線でそれぞれ表す。このとき，③のグラフの移動の様子を示すと $\boxed{\boxed{\enspace\textsf{オ}\enspace}}$ となり，④のグラフの移動の様子を示すと $\boxed{\boxed{\enspace\textsf{カ}\enspace}}$ となる。

$\boxed{\boxed{\enspace\text{オ}\enspace}}$，$\boxed{\boxed{\enspace\text{カ}\enspace}}$ については，最も適当なものを，次の $\textsf{\textcircled{0}}$ ～ ⑦ のうちから一つずつ選べ。ただし，同じものを繰り返し選んでもよい。なお，$x$ 軸と $y$ 軸は省略しているが，$x$ 軸は右方向，$y$ 軸は上方向がそれぞれ正の方向である。

(4) $\boxed{\enspace\text{ウ}\enspace}<q<\boxed{\enspace\text{エ}\enspace}$ とする。全体集合 $U$ を実数全体の集合とし，$U$ の部分集合 $A$，$B$ を

$A=\{x|x^2-6x+q<0\}$
$B=\{x|x^2+qx-6<0\}$

とする。$U$ の部分集合 $X$ に対し，$X$ の補集合を $\overline{X}$ と表す。このとき，次のことが成り立つ。

・$x\in A$ は，$x\in B$ であるための $\boxed{\boxed{\enspace\textsf{キ}\enspace}}$。

・$x\in B$ は，$x\in\overline{A}$ であるための $\boxed{\boxed{\enspace\textsf{ク}\enspace}}$。

$\boxed{\boxed{\enspace\text{キ}\enspace}}$，$\boxed{\boxed{\enspace\text{ク}\enspace}}$ の回答群（同じものを繰り返し選んでもよい。）

〔２〕

日本国外における日本語教育の状況を調べるために独立行政法人国際交流基金では｢海外日本語教育機関調査｣を実施しており，各国における教育機関数，教員数，学習者数が調べられている。 2018年度において学習者数が5000人以上の国と地域(以下，国)は29か国であった。これら29か国について，2009年度と2018年度のデータが得られている。
(1)　各国において，学習者数を教員数で割ることにより，国ごとの｢教員１人あたりの学習者数｣を算出することができる。図１と図２は，2009年度および2018年度における｢教員１人あたりの学習者数｣のヒストグラムである。これら二つのヒストグラムから，９年間の変化に関して，後のことが読み取れる。なお，ヒストグラムの各階級の区間は，左側の数値を含み，右側の数値を含まない。

・2009年度と2018年度の中央値が含まれる階級の階級値を比較すると，$\boxed{\boxed{\enspace\textsf{ケ}\enspace}}$。

・2009年度と2018年度の第１四分位数が含まれる階級の階級値を比較すると，$\boxed{\boxed{\enspace\textsf{コ}\enspace}}$。

・2009年皮と2018年度の第３四分位数が含まれる階級の階級値を比較すると，$\boxed{\boxed{\enspace\textsf{サ}\enspace}}$。

・2009年度と2018年度の範囲を比較すると，$\boxed{\boxed{\enspace\textsf{シ}\enspace}}$。

・2009年度と2018年度の四分位範囲を比較すると，$\boxed{\boxed{\enspace\textsf{ス}\enspace}}$。

$\boxed{\boxed{\enspace\text{ケ}\enspace}}$ ～ $\boxed{\boxed{\enspace\text{ス}\enspace}}$ の解答群(同じものを繰り返し選んでもよい。)

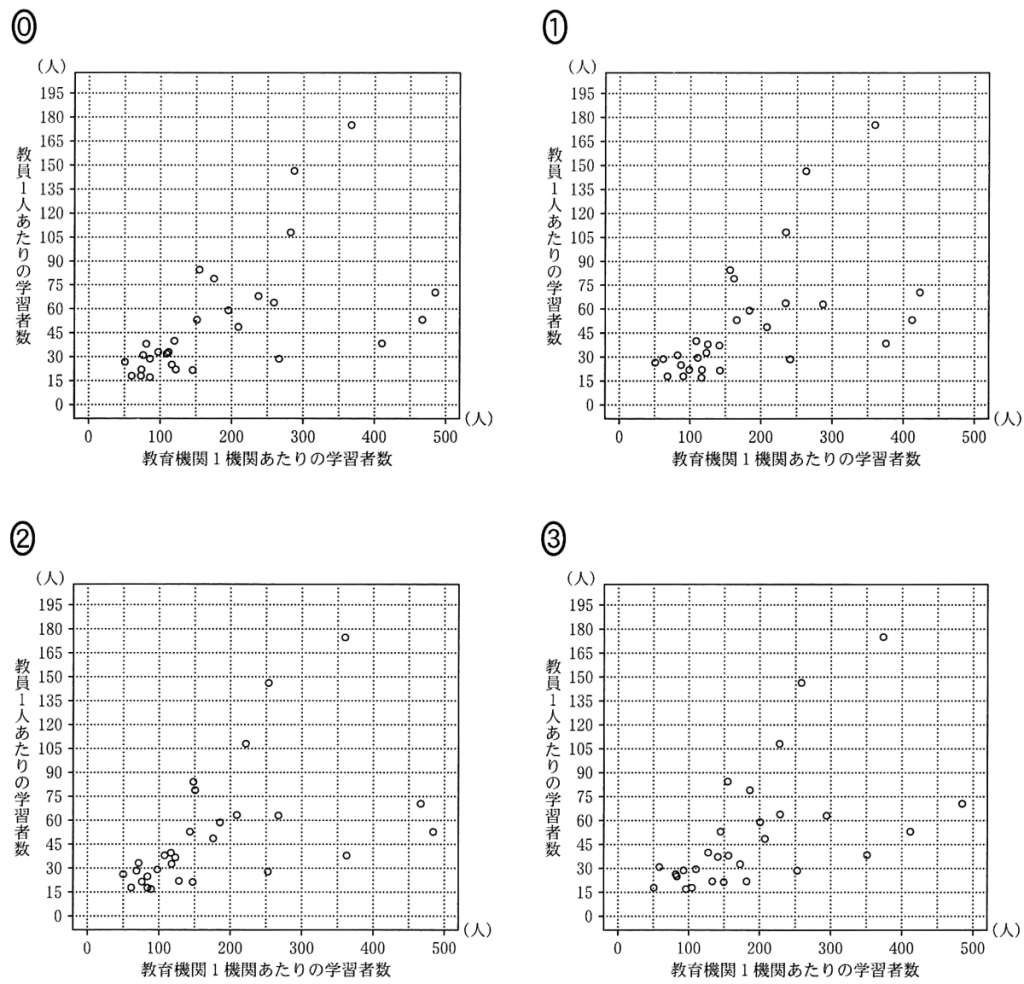
(2)　各国において，学習者数を教育機関数で割ることにより，｢教育機関１機関あたりの学習者数｣も算出した。図３は，2009年度における｢教育機関１幾関あたりの学習者数｣の箱ひげ図である。

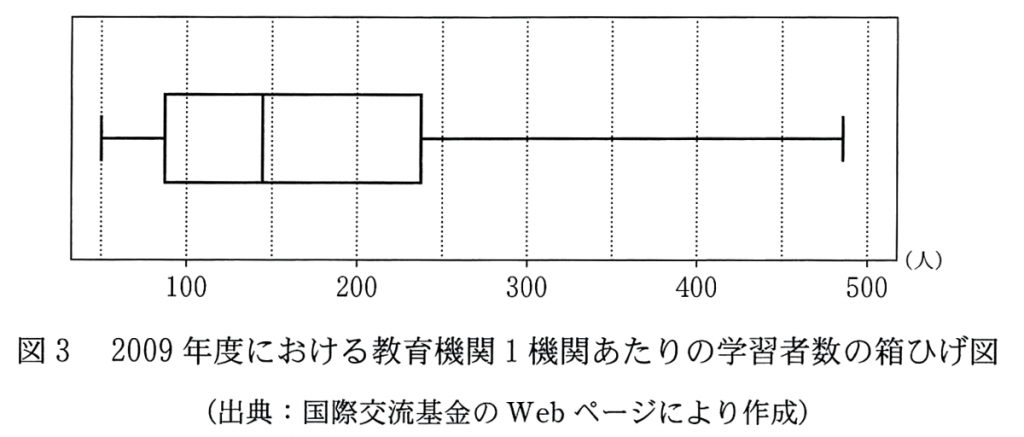
2009年度について，｢教育機関１機関あたりの学習者数｣(横軸)と｢教員１人あたりの学習者数｣(縦軸)の散布図は $\boxed{\boxed{\enspace\textsf{セ}\enspace}}$ である。ここで，2009年度における｢教員１人あたりの学習者数｣のヒストグラムである(1)の図１を，図４として再掲しておく。

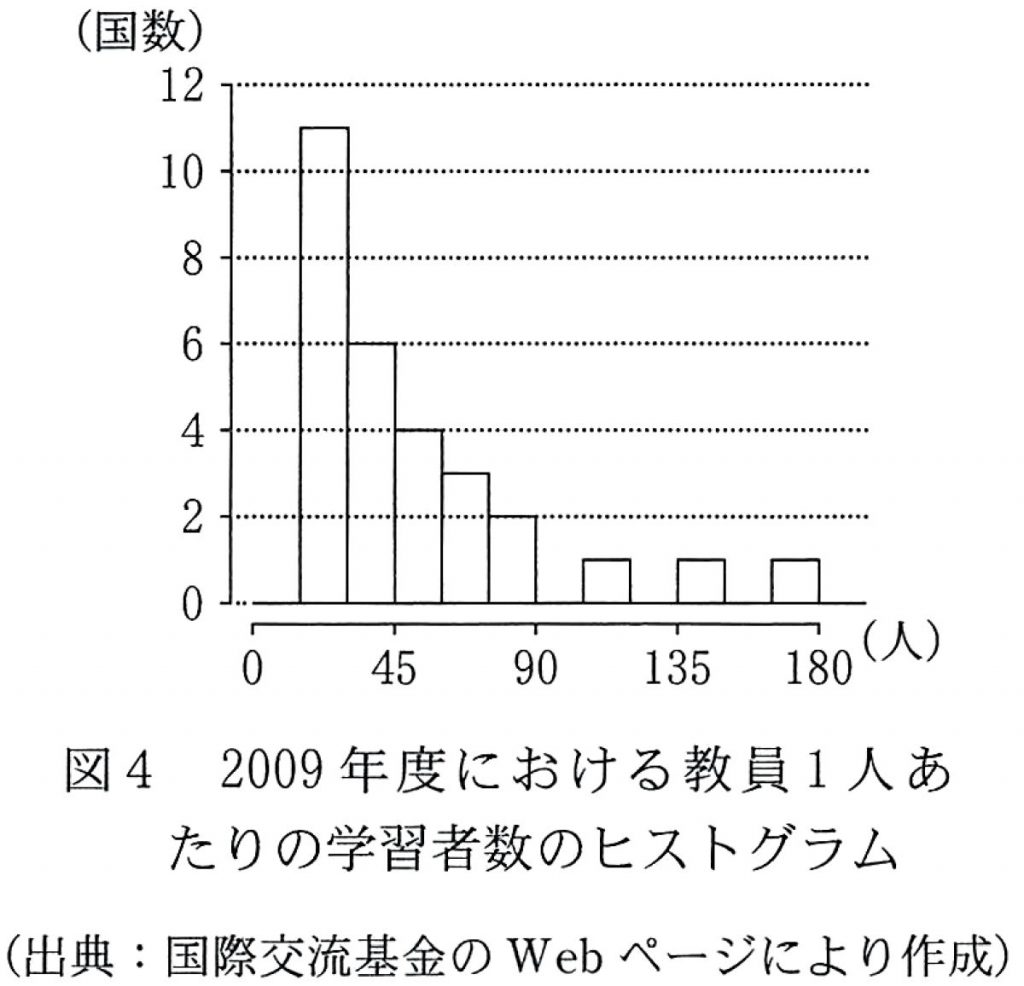
$\boxed{\boxed{\enspace\text{セ}\enspace}}$ については，最も適当なものを，次の $\textsf{\textcircled{0}}$ ～ ③ のうちから一つ選べ。なお，これらの散布図には，完全に重なっている点はない。

(3)　各国における2018年度の学習者数を100としたときの2009年度の学習者数 $S$，および，各国における2018年度の教員数を100としたときの2009年度の教員数 $T$ を算出した。
例えば，学習者数について説明すると，ある国において，2009年度が44272人，2018年度が174521人であった場合，2009年度の学習者数 $S$ は $\cfrac{44272}{174521}\times100$ より25.4と算出される。
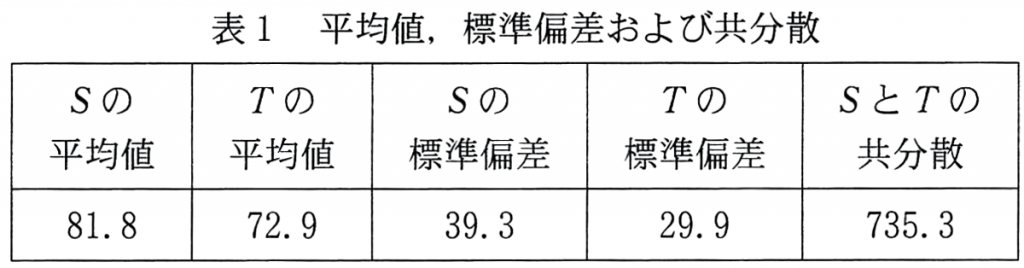
表１は $S$ と $T$ について，平均値，標準偏差および共分散を計算したものである。ただし，$S$ と $T$ の共分散は，$S$ の偏差と $T$ の偏差の積の平均値である。
表１の数値が四捨五入していない正確な値であるとして，$S$ と $T$ の相関係数を求めると $\boxed{\enspace\textsf{ソ}\enspace}.\boxed{\enspace\textsf{タチ}\enspace}$ である。

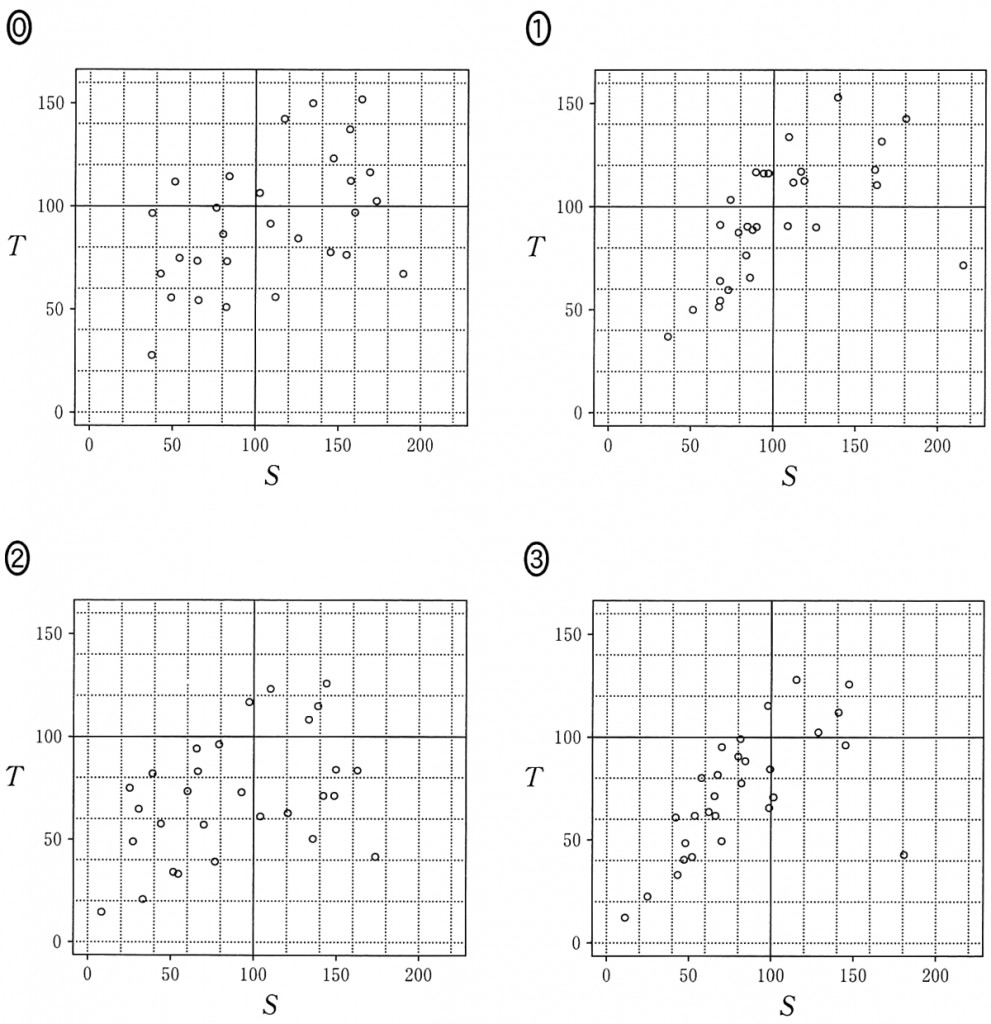
(4)　表１と(3)で求めた相関係数を参考にすると，(3)で算出した2009年度の $S$(横軸)と $T$(縦軸)の散布図は $\boxed{\boxed{\enspace\textsf{ツ}\enspace}}$ である。

$\boxed{\boxed{\enspace\text{ツ}\enspace}}$ については，最も適当なものを，次の $\textsf{\textcircled{0}}$ ～③のうちから一つ選べ。なお，これらの散布図には，完全に重なっている点はない。