【スマホで読む・わかりやすい】共通テスト数学IA2022本試【解説・正解・問題】

第１問　正解

アイ $-6$　ウエ $38$　オカ $-2$
キク $18$　ケ $2$　コ.サシス $0.072$
セ $2$　ソ,タ 2, 3　チツ,テ 10, 3
ト 4　ナ 6　ニヌ,ネ $-1$, 3
ノ,ハ 7, 3　ヒ 4

〔１〕(1)

公式に①，②を代入して

$1^2=13+2ab+2bc+2ca$
$2ab+2bc+2ca=-12$
$ab+bc+ca=-6$

・・・アイ

$(a-b)^2+(b-c)^2+(c-a)^2$
$=a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2$
$=2a^2+2b^2+2c^2-2ab-2bc-2ca$
$2(a^2+b^2+c^2)-2(ab+bc+ca)$

$a^2+b^2+c^2=13$ と $ab+bc+ca=-6$ を代入して

$2\times13-2\times(-6)=38$

・・・ウエ

〔１〕(2)

$x+y=b-c+c-a$
$=b-a$
$=-(a-b)$
$=-2\sqrt{5}$

・・・オカ

次に，(1)の計算を利用して $x^2+y^2$ を求める。

$x^2+y^2=(b-c)^2+(c-a)^2$

となる。(1)より

$(a-b)^2+(b-c)^2+(c-a)^2=38$

$a-b=2\sqrt{5}$ を代入すると

$(2\sqrt{5})^2+(b-c)^2+(c-a)^2=38$
$20+(b-c)^2+(c-a)^2=38$
$(b-c)^2+(c-a)^2=18$

となるので

$x^2+y^2=18$

・・・キク

これらより

$(a-b)(b-c)(c-a)$

を求める。

問題文より $a-b=2\sqrt{5}$，$b-c=x$，$c-a=y$ をそれぞれ代入すると

$=2\sqrt{5}xy$

ここで

$(x+y)^2=x^2+2xy+y^2$ より

$2xy=(x+y)^2-(x^2+y^2)$

$x+y=-2\sqrt{5}$，$x^2+y^2=18$ をそれぞれ代入すると

$2xy=(-2\sqrt{5})^2-18$
$=20-18$
$=2$

よって

$xy=1$

これを $2\sqrt{5}xy$ に代入すると

$(a-b)(b-c)(c-a)=2\sqrt{5}$

・・・ケ

〔２〕

三角比の表より $\tan16\degree=0.2867$ であり

$\text{AC}:\text{BC}=1:0.2867$

である。

しかし，実際には水平方向と鉛直方向で縮尺が異なる。$\cfrac{1}{25000}$ の縮尺は $\cfrac{1}{4}$ 倍すれば $\cfrac{1}{100000}$ の縮尺となるので

$0.2867\times\cfrac{1}{4}=0.0716\cdots$

ここで，問題冊子の「Ⅱ 解答上の注意」に一つ下の桁を四捨五入するように指示があることに注意して

$\tan\angle\text{BAC}=0.072$

・・・コサシス

次に，∠BAC の大きさを求めると，三角比の表より

$0.0699<0.072<0.0875$
$\tan4\degree<\tan\angle\text{BAC}<\tan5\degree$

したがって，∠BAC の大きさは，② 4° より大きく 5° より小さい。

・・・セ

〔３〕(1)

$\sin\angle\text{ABC}$ を求める。

外接円の半径は 3 だから，正弦定理より

$\cfrac{4}{\sin\angle\text{ABC}}=2\times3=6$

$\sin\angle\text{ABC}=\cfrac{4}{6}$
$=\cfrac{2}{3}$

・・・ソタ

次に，AD を求める。

ここで，三角比の性質を考えると良い。

$\sin$ は $\cfrac{\textsf{高さ}}{\textsf{斜辺}}$ だから

$\textsf{斜辺}\times\sin\theta=\textsf{斜辺}\times\cfrac{\textsf{高さ}}{\textsf{斜辺}}$
$=\cancel{\textsf{斜辺}}\times\cfrac{\textsf{高さ}}{\cancel{\textsf{斜辺}}}$
$=\textsf{高さ}$

となり，高さを求めることができる。

これを利用して

$\text{AD}=\text{AB}\times\sin\angle\text{ABD}$
$=5\sin\angle\text{ABD}$

$\angle\text{ABD}=\angle\text{ABC}$ だから

$=5\times\cfrac{2}{3}=\cfrac{10}{3}$

・・・チツテ

〔３〕(2)

外接円の半径が 3 であることに注意する。つまり，外接円の直径は 6 となるので，三角形のそれぞれの辺の長さの最大は 6 である。

よって

$0\leqq\text{AC}\leqq6$

また，$2\text{AB}+\text{AC}=14$ より

$\text{AC}=14-2\text{AB}$

これを代入して

$0\leqq14-2\text{AB}\leqq6$

たとえば $1\leqq2$ の符号を逆にすると $-1\geqq-2$ となるように，プラス・マイナスを入れかえると不等号の向きが逆になることに注意して

$-6\leqq2\text{AB}-14\leqq0$
$8\leqq2\text{AB}\leqq14$
$4\leqq\text{AB}\leqq7$

ただし，辺の長さの最大は 6 だから

$4\leqq\text{AB}\leqq6$

・・・ト,ナ

次に AD を AB の式で表す。

正弦定理より

$\cfrac{\text{AC}}{\sin\angle\text{ABC}}=2\times3=6$
$\sin\angle\text{ABC}=\cfrac{\text{AC}}{6}$

また，$\textsf{斜辺}\times\sin\theta=\textsf{高さ}$ を用いて

$\text{AB}\times\sin\angle\text{ABD}=\text{AD}$

$\angle\text{ABC}=\angle\text{ABD}$ だから

$\text{AB}\times\cfrac{\text{AC}}{6}=\text{AD}$
$\text{AB}\times\text{AC}=6\text{AD}$

$\text{AC}=14-2\text{AB}$ より

$\text{AB}(14-2\text{AB})=6\text{AD}$
$14\text{AB}-2\text{AB}^2=6\text{AD}$
$\text{AD}=\cfrac{-1}{3}\text{AB}^2+\cfrac{7}{3}\text{AB}$

・・・ニヌネノハ

さらに，AD の最大値を求める。

$\text{AB}=x$，$\text{AD}=y$ とすると

$y=-\cfrac{1}{3}x^2+\cfrac{7}{3}x$

平方完成して

$y=-\cfrac{1}{3}(x^2-7x)$
$=-\cfrac{1}{3}\Big(x-\cfrac{7}{2}\Big)^2+\cfrac{49}{12}$

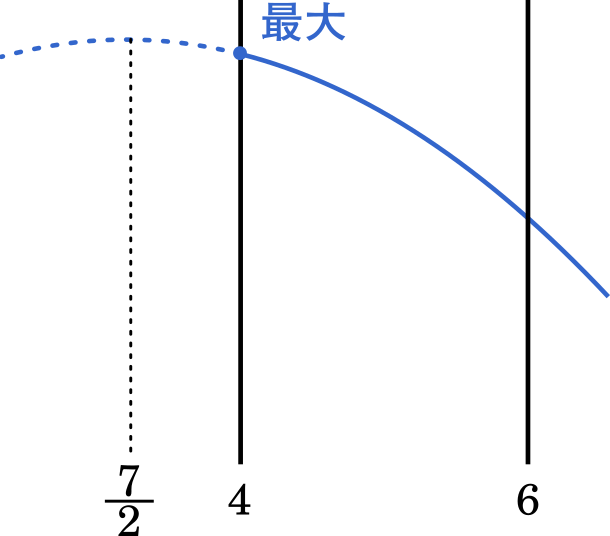
よって，$y$ の最大は $x=4$ のとき。

$y=-\cfrac{1}{3}x^2+\cfrac{7}{3}x$ に $x=4$ を代入すると

$y=-\cfrac{1}{3}\times4^2+\cfrac{7}{3}\times4$
$=\cfrac{-16+28}{3}$
$=\cfrac{12}{3}$
$=4$

したがって，AD の長さの最大値は 4 である。

・・・ヒ

問題文

第１問〔１〕

実数 $a,b,c$ が

$a+b+c=1$ ・・・①

および

$a^2+b^2+c^2=13$ ・・・②

を満たしているとする。

(1) $(a+b+c)^2$ を展開した式において，① と ② を用いると

$ab+bc+ca=\boxed{\textsf{\enspace アイ\enspace}}$

であることがわかる。よって

$(a-b)^2+(b-c)^2+(c-a)^2=\boxed{\textsf{\enspaceウエ\enspace}}$

である。

(2) $a-b=2\sqrt{5}$ の場合に，$(a-b)(b-c)(c-a)$ の値を求めてみよう。

$b-c=x$，$c-a=y$ とおくと

$x+y=\boxed{\textsf{\enspace オカ\enspace}}\sqrt{5}$

である。また，(1)の計算から

$x^2+y^2=\boxed{\textsf{\enspace キク\enspace}}$

が成り立つ。

これらより

$(a-b)(b-c)(c-a)=\boxed{\textsf{\enspace ケ\enspace}}\sqrt{5}$

である。

〔２〕

以下の問題を解答するにあたっては，必要に応じて 41 ページの三角比の表を用いてもよい。

太郎さんを花子さんは，キャンプ場のガイドブックにある地図を見ながら，後のように話している。

太郎：キャンプ場の地点 A から山頂 B を見上げる角度はどれくらいかな。

花子：地図アプリを使って，地点 A と山頂 B を含む断面図を調べたら，図 1 のようになったよ。点 C は，山頂 B から地点 A を通る水平面に下ろした垂線とその水平面との交点のことだよ。

太郎：図 1 の角度 $\theta$ は，AC，BC の長さを定規で測って，三角比の表を用いて調べたら 16° だったよ。

花子：本当に 16° なの？　図 1 の鉛直方向の縮尺と水平方向の縮尺は等しいのかな？

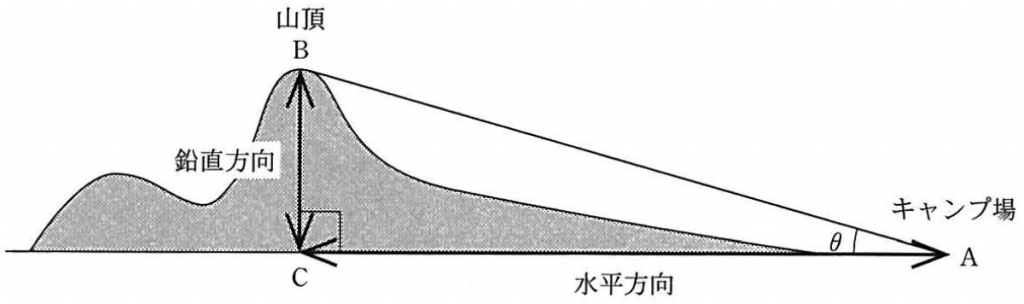
図 1 の $\theta$ はちょうど 16° であったとする。しかし，図 1 の縮尺は，水平方向が $\cfrac{1}{100000}$ であるのに対して，鉛直方向は $\cfrac{1}{25000}$ であった。

実際にキャンプ場の地点 A から山頂 B を見上げる角である ∠BAC を考えると，$\tan\angle\text{BAC}$ は $\boxed{\textsf{\enspace コ\enspace}}.\boxed{\textsf{\enspace サシス\enspace}}$ となる。したがって，∠BAC の大きさは $\boxed{\boxed{\textsf{\enspace セ\enspace}}}$。ただし，目の高さは無視して考えるものとする。

$\boxed{\boxed{\textsf{\enspace セ\enspace}}}$ の回答群

三角比の表

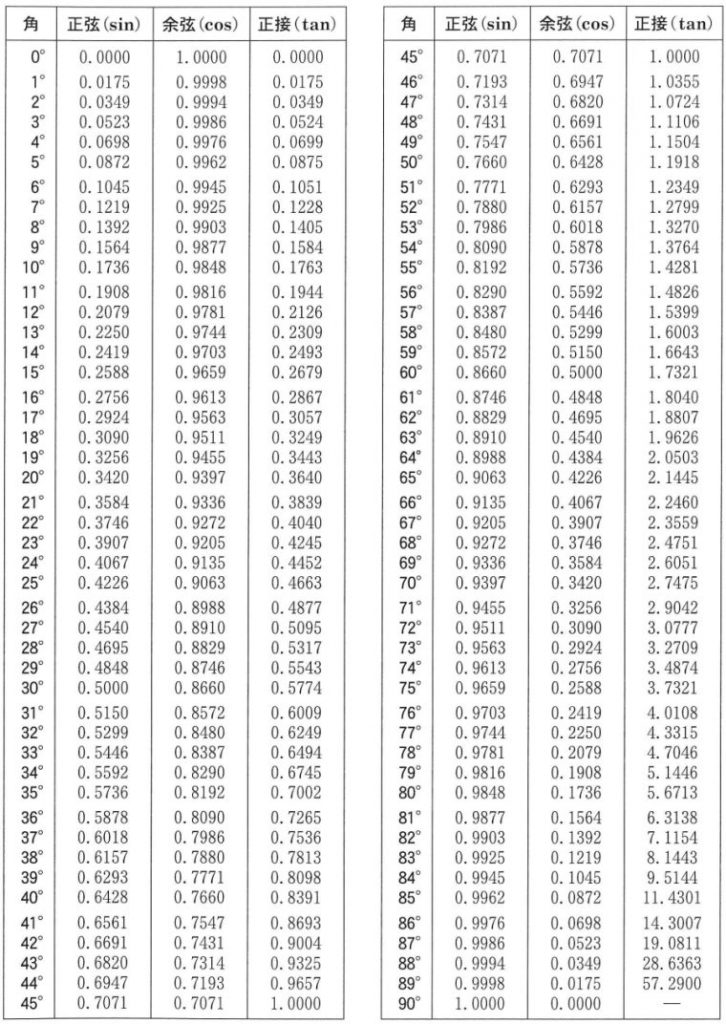
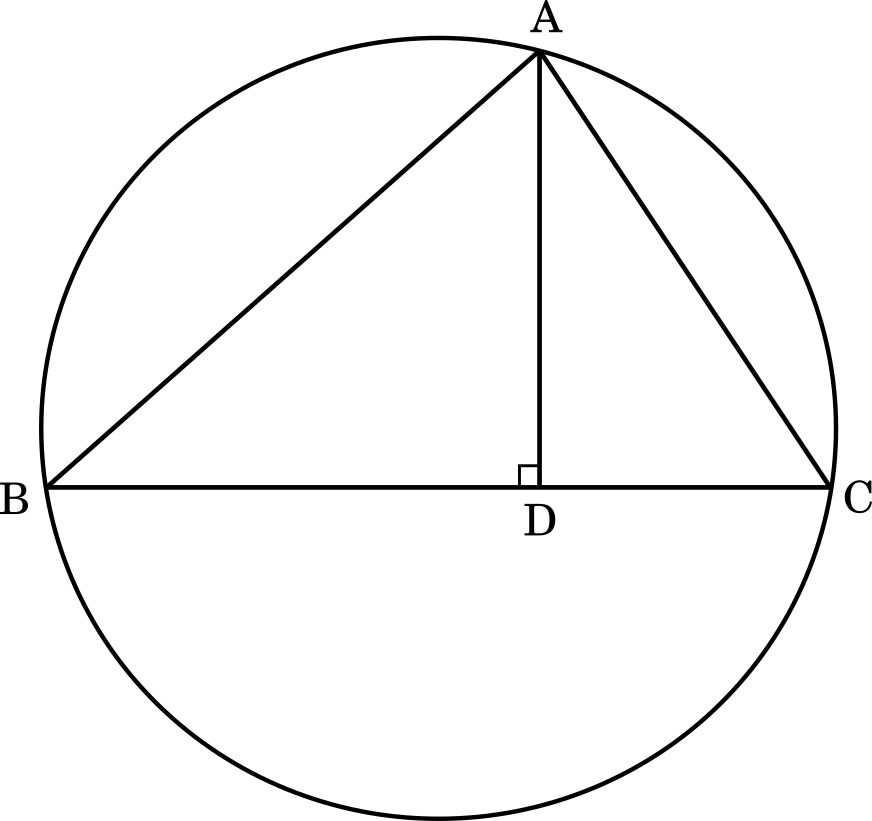
〔3〕外接円の半径が 3 である △ABC を考える。点 A から直線 BC に引いた垂線と直線 BC との交点を D とする。

(1) $\text{AB}=5$，$\text{AC}=4$ とする。このとき

$\sin\angle\text{ABC}=\cfrac{\boxed{\textsf{\enspace ソ\enspace}}}{\boxed{\textsf{\enspace タ\enspace}}}$，$\text{AD}=\cfrac{\boxed{\textsf{\enspace チツ\enspace}}}{\boxed{\textsf{\enspace テ\enspace}}}$

である。

(2) 2 辺 AB，AC の長さの間に 2AB + AC = 14 の関係があるとする。

このとき，AB の長さのとり得る値の範囲は $\boxed{\textsf{\enspace ト\enspace}}\leqq\text{AB}\leqq\boxed{\textsf{\enspace ナ\enspace}}$ であり

$\text{AD}=\cfrac{\space\boxed{\textsf{\enspace ニヌ\enspace}}\space}{\boxed{\textsf{\enspace ネ\enspace}}}\space\text{AB}^2+\cfrac{\space\boxed{\textsf{\enspace ノ\enspace}}\space}{\boxed{\textsf{\enspace ハ\enspace}}}\space\text{AB}$

と表せるので，AD の長さの最大値は $\boxed{\enspace\textsf{ヒ}\enspace}$ である。