【数IIBベクトル】直角三角形の辺の比を利用して内部点を求める融合問題(千葉大2019第5問)
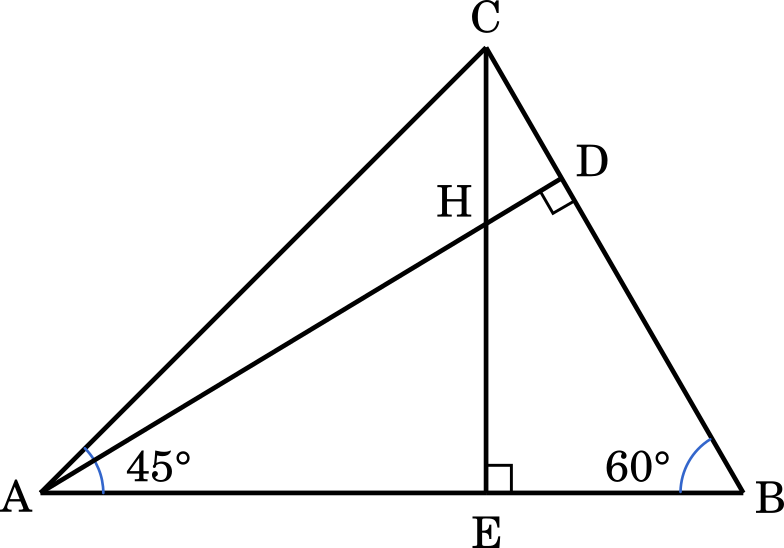
三角形 ABC において $\angle\text{A}=45\degree,\angle\text{B}=60\degree$ である。頂点 A から辺 BC に引いた垂線と BC が交わる点を D とし,頂点 C から辺 AB に引いた垂線と AB が交わる点を E とする。また,$\vec{a}=\overrightarrow{\text{CA}}$,$\vec{b}=\overrightarrow{\text{CB}}$ とする。このとき以下の問いに答えよ。
(1) $\overrightarrow{\text{CE}}$ を $\vec{a}$,$\vec{b}$ を用いて表わせ。
(2) 直線 CE と直線 AD の交点を H とするとき,$\overrightarrow{\text{CH}}$ を $\vec{a}$,$\vec{b}$ を用いて表わせ。
内分点を求める
(1) $\overrightarrow{\text{CE}}$ を $\vec{a}$,$\vec{b}$ を用いて表わせ。
点 E は AB の内分点です。もし,$m:n$ で内分なら
$\overrightarrow{\text{CE}}=\cfrac{n\vec{a}+m\vec{b}}{m+n}$
と表すことができます。
そこで,AE : BE を求めてみましょう。
まず,△ACE は辺の比が $1:1:\sqrt{2}$,△BCE は $1:2:\sqrt{3}$ の三角形です。
$\text{AE}:\text{CE}=1:1$ ・・・①
$\text{BE}:\text{CE}=1:\sqrt{3}$ ・・・②
①× $\sqrt{3}$
$\text{AE}:\text{CE}=\sqrt{3}:\sqrt{3}$ ・・・①’

①’,②より
$\text{AE}:\text{BE}=\sqrt{3}:1$
したがって
$\overrightarrow{\text{CE}}=\cfrac{\vec{a}+\sqrt{3}\vec{b}}{\sqrt{3}+1}$
内分点の求め方
(2) 直線 CE と直線 AD の交点を H とするとき,$\overrightarrow{\text{CH}}$ を $\vec{a}$,$\vec{b}$ を用いて表わせ。

$\overrightarrow{\text{CE}}$ を $k$ 倍したものを $\overrightarrow{\text{CH}}$とすると
$\overrightarrow{\text{CH}}=k\overrightarrow{\text{CE}}$ ・・・①
AD を $t:1-t$ で内分した点を H とすると
$\overrightarrow{\text{CH}}=(1-t)\vec{a}+t\overrightarrow{\text{CD}}$ ・・・②
と表すことができます。あとは 2 つの式を連立して $k$ を求めていく流れです。
まず,CD の長さがわからないので求めていきましょう。
(1)より
$\text{AB}:\text{EB}=\sqrt{3}+1:1$
また,△BCE において
$\text{EB}:\text{CB}=1:2$
だから
$\text{AB}:\text{CB}=\sqrt{3}+1:2$ ・・・③
△ABD において
$\text{AB}:\text{DB}=2:1$
だから,$\sqrt{3}+1$ 倍すると
$\text{AB}:\text{DB}=2\sqrt{3}+2:\sqrt{3}+1$ ・・・④
③を
$\text{AB}:\text{CB}=2\sqrt{3}+2:4$ ・・・③’
とすると,③’,④より
$\text{CB}:\text{DB}=4:\sqrt{3}+1$
$4\text{DB}=(\sqrt{3}+1)\text{CB}$
$\text{DB}=\cfrac{\sqrt{3}+1}{4}\text{CB}$
よって
$\text{CD}=\Big(1-\cfrac{\sqrt{3}+1}{4}\Big)\text{CB}$
$=\Big(\cfrac{4-\sqrt{3}-1}{4}\Big)\text{CB}$
$=\cfrac{3-\sqrt{3}}{4}\text{CB}$
これより①,②は
$\overrightarrow{\text{CH}}=k\cdot\cfrac{\vec{a}+\sqrt{3}\vec{b}}{\sqrt{3}+1}$ ・・・①
$\overrightarrow{\text{CH}}=(1-t)\vec{a}+\cfrac{3-\sqrt{3}}{4}t\vec{b}$ ・・・②’
となります。係数をそれぞれ比べると
$\cfrac{k}{\sqrt{3}+1}=1-t$ ・・・⑤
$\cfrac{\sqrt{3}k}{\sqrt{3}+1}=\cfrac{3-\sqrt{3}}{4}t$ ・・・⑥
という関係が成り立ちます。
ここから $k$ を求めていきましょう。
⑤より
$t=1-\cfrac{k}{\sqrt{3}+1}$
⑥に代入
$\cfrac{\sqrt{3}k}{\sqrt{3}+1}=\cfrac{3-\sqrt{3}}{4}\Big(1-\cfrac{k}{\sqrt{3}+1}\Big)$
$=\cfrac{3-\sqrt{3}}{4}-\cfrac{3-\sqrt{3}}{4(\sqrt{3}+1)}k$
$=\cfrac{3-\sqrt{3}}{4}-\cfrac{3-\sqrt{3}}{4(\sqrt{3}+1)}k$
$\Big\{\cfrac{\sqrt{3}}{\sqrt{3}+1}+\cfrac{3-\sqrt{3}}{4(\sqrt{3}+1)}\Big\}k=\cfrac{3-\sqrt{3}}{4}$
$\cfrac{4\sqrt{3}+3-\sqrt{3}}{4(\sqrt{3}+1)}k=\cfrac{3-\sqrt{3}}{4}$
$\cfrac{3\sqrt{3}+3}{4(\sqrt{3}+1)}k=\cfrac{3-\sqrt{3}}{4}$
$\cfrac{3(\sqrt{3}+1)}{4(\sqrt{3}+1)}k=\cfrac{3-\sqrt{3}}{4}$
$\cfrac{3}{4}k=\cfrac{3-\sqrt{3}}{4}$
$3k=3-\sqrt{3}$
$k=\cfrac{3-\sqrt{3}}{3}$
よって
$\overrightarrow{\text{CH}}=\cfrac{3-\sqrt{3}}{3}\cdot\cfrac{\vec{a}+\sqrt{3}\vec{b}}{\sqrt{3}+1}$
$=\cfrac{(3-\sqrt{3})(\sqrt{3}-1)}{3(\sqrt{3}+1)(\sqrt{3}-1)}(\vec{a}+\sqrt{3}\vec{b})$
$=\cfrac{3\sqrt{3}-3-3+\sqrt{3}}{3(3-1)}(\vec{a}+\sqrt{3}\vec{b})$
$=\cfrac{4\sqrt{3}-6}{6}(\vec{a}+\sqrt{3}\vec{b})$
$=\cfrac{2\sqrt{3}-3}{3}(\vec{a}+\sqrt{3}\vec{b})$ (答え)
SNSでシェア