【数IIB】絶対値のついた 2 次関数と解の個数を求める（千葉大2019第2問）

グラフを描く

$m=1$ とすると

$y=|x^2-2x|-1$

絶対値の中身が正のときと負のときでわけて考えましょう。

(i) $x^2-2x\geqq0$ のとき

$x(x-2)\geqq0$
$x\leqq0,x\geqq2$

また

$y=x^2-2x-1$

平方完成して頂点の座標を求めます。

$=(x-1)^2-2$

$x$ 軸との交点を求めます。

$x^2-2x-1=0$ とすると
$x=1\pm\sqrt{1+1}=1\pm\sqrt{2}$

(ii) $x^2-2x<0$ のとき

$x$ の範囲は，$0<x<2$ です。

$y=-x^2+2x-1$
$=-(x^2-2x)-1$
$=-(x-1)^2$

頂点が (1,0) になるので，これが $x$ 軸との交点になります。

したがって

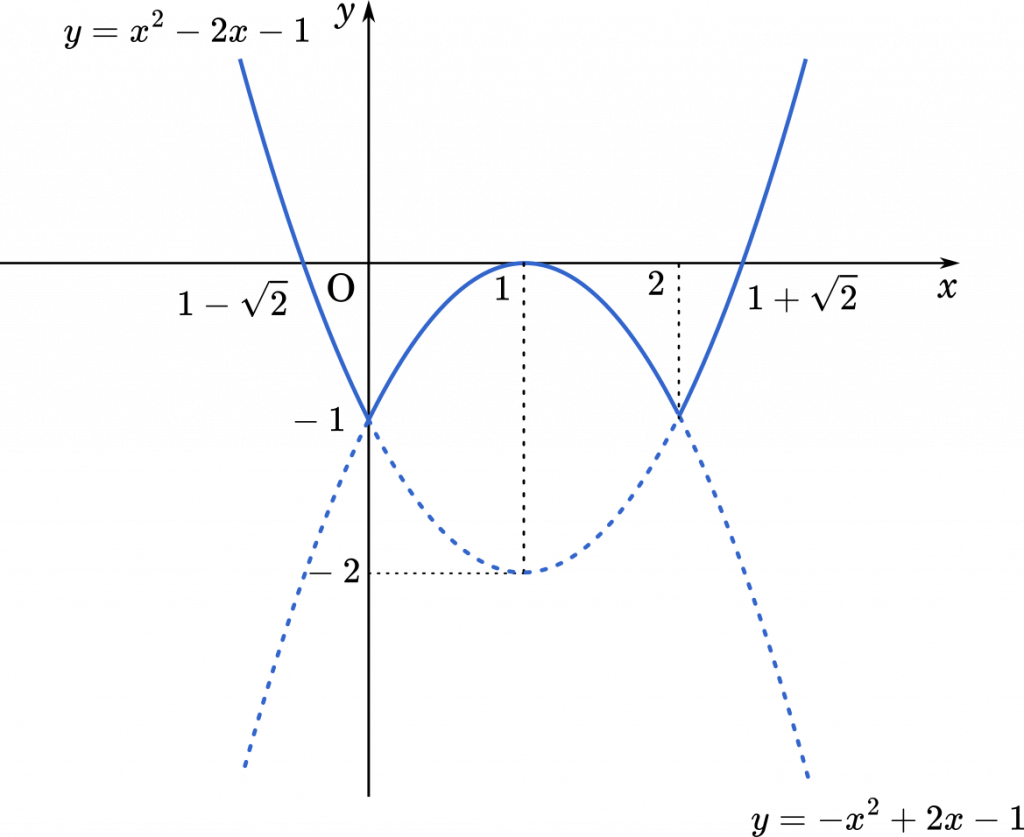
2 次関数の解の個数を考える

この問題は，$|x^2-2mx|-m=0$ の解の個数を求めることと同じです。これを変形して

$|x^2-2mx|=m$

としておきます。

(i) $m<0$ のとき

$|x^2-2mx|\geqq0$

$|x^2-2mx|=m$ を考えると，右辺がマイナスで左辺が 0 以上の値とすると，この方程式を満たす $x$ はありません。

よって，共有点は 0 個。

(ii) $m=0$ のとき

$|x^2-2mx|=m$ は

$|x^2|=0$
$x=0$

共有点は 1 個。

(iii) $m>0$ のとき

この場合は少し考える必要があります。

$y=|x^2-2mx|$ として

$x^2-2mx\geqq0$ のとき

$x(x-2m)\geqq0$
$x\leqq0,x\geqq2m$

平方完成して

$y=x^2-2mx$
$=(x-m)^2-m^2$

頂点の座標は $(m,-m^2)$ です。

また，$x^2-2mx<0$ のとき
$0<x<2m$

$y=-x^2+2mx$
$=-(x^2-2mx)$
$=-(x-m)^2+m^2$

頂点の座標は $(m,m^2)$ です。

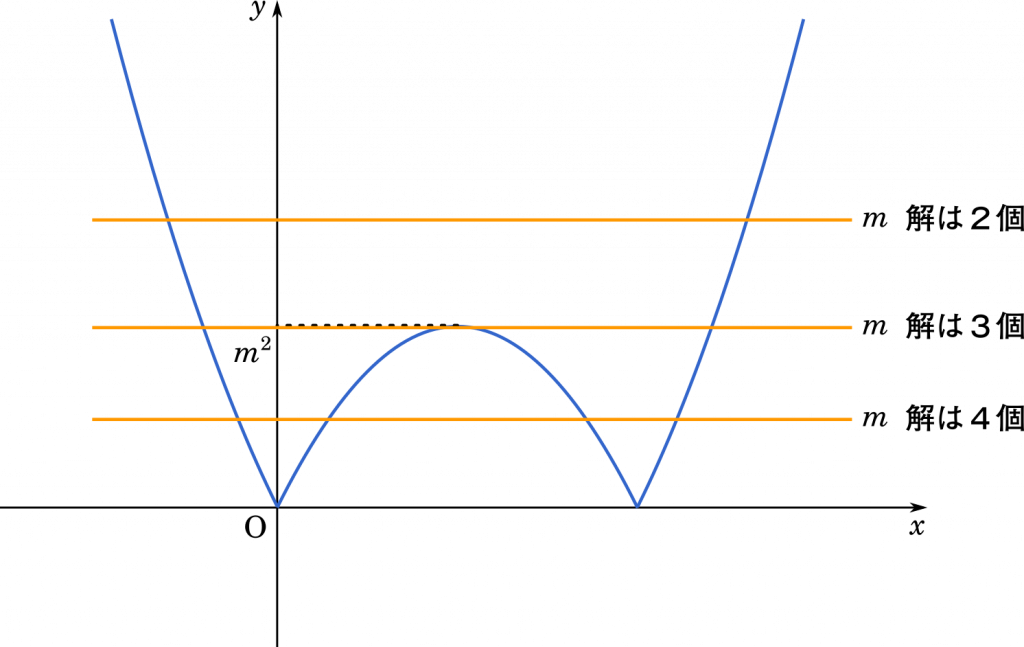
$m$ の値によって共有点の個数が変わります。

$0<m<m^2$ のとき

グラフから，共有点は 4 個です。$m$ の範囲を求めましょう。

不等式を変形すると

$m^2-m>0$
$m(m-1)>0$
$m<0,m>1$
$m<0$ は不適なので，$m>1$

$m=m^2$ のとき

共有点は 3 個です。

$m^2-m=0$
$m(m-1)=0$
$m=0,1$

$m=0$ は不適なので，$m=1$

$m>m^2$ のとき

共有点は 2 個です。

$m^2-m<0$
$m(m-1)<0$
$0<m<1$

以上をまとめると

$m<0$ のとき，共有点は 0 個。
$m=0$ のとき，共有点は 1 個。
$0<m<1$ のとき，共有点は 2 個。
$m=1$ のとき，共有点は 3 個。
$m>1$ のとき，共有点は 4 個。
（答え）