【数IIBベクトル・数列】回転しながら移動する点の座標を求める(千葉大2020第3問)
座標平面上に 4 点 $\text{P}_0(2,0),\text{P}_1(0,2),\text{Q}_0(0,0),\text{Q}_1(-1,1)$ がある。正の整数 $n$ に対し,点 $\text{P}_n$,$\text{Q}_n$ まで定まったとき,点 $\text{P}_{n+1},\text{Q}_{n+1}$ を以下の条件で定める。
四角形 $\text{P}_n\text{P}_{n+1}\text{Q}_{n+1}\text{Q}_n$ と四角形 $\text{P}_{n-1}\text{P}_n\text{Q}_n\text{Q}_{n-1}$ は相似であり,かつ辺 $\text{P}_n\text{Q}_n$ のみを共有する。
このとき以下の問いに答えよ。
(1) $\text{P}_2,\text{Q}_2$ の座標を求めよ。
(2) $\text{P}_4,\text{P}_8$ の座標を求めよ。
(3) 正の整数 $m$ に対して,$\text{P}_{8m}$ の座標を $m$ の式で表せ。
相似比を求める
(1) $\text{P}_2,\text{Q}_2$ の座標を求めよ。
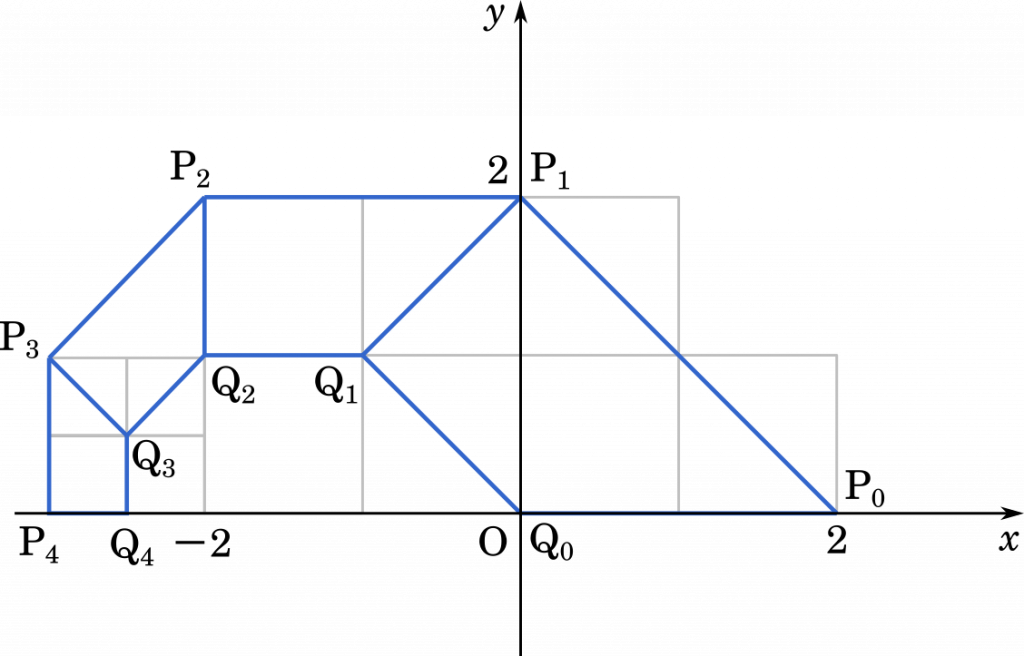
問題文の条件にしたがって図を描くと上のようになります。台形が徐々に小さくなりながらつながっています。
まず,台形の相似比を考えましょう。
点 $\text{P}_n$ と $\text{Q}_n$ をむすぶ辺の長さを $\text{P}_n\text{Q}_n$ と表すと
$\text{P}_0\text{Q}_0:\text{P}_1\text{Q}_1=2:\sqrt{2}$
となるので,台形どうしの相似比は $2:\sqrt{2}$ です。
また
$2\text{P}_1\text{Q}_1=\sqrt{2}\text{P}_0\text{Q}_0$
$\text{P}_1\text{Q}_1=\cfrac{\sqrt{2}}{2}\text{P}_0\text{Q}_0$
となるので
$\text{P}_{n+1}\text{Q}_{n+1}=\cfrac{\sqrt{2}}{2}\text{P}_n\text{Q}_n$
という関係が成り立ちます。よって
他の辺の長さも同様に求めることができるので
$\text{P}_1\text{P}_2=\cfrac{\sqrt{2}}{2}\text{P}_0\text{P}_1$
$=\cfrac{\sqrt{2}}{2}\cdot2\sqrt{2}=2$
$\text{Q}_1\text{Q}_2=\cfrac{\sqrt{2}}{2}\text{Q}_0\text{Q}_1$
$=\cfrac{\sqrt{2}}{2}\cdot\sqrt{2}=1$
あとは,グラフ上に点をおいてみると座標がわかります。
したがって
$\text{P}_2(-2,2),\text{Q}_2(-2,1)$ (答え)
n が偶数であるときの特徴をとらえる
(2) $\text{P}_4,\text{P}_8$ の座標を求めよ。
(1)と同様の計算をしていけば $\text{P}_4,\text{P}_8$ が求められるのですが,アイデアをもう少し整理しましょう。
台形は $n$ の値が 1 つ増えるごとに 45° ずつ回転します。$n$ が値が 2 つ増えたら 90° 回転です。
そこで,$\text{P}_0\text{P}_2$ を縮小して 90° 回転したものを $\text{P}_2\text{P}_4$ というように考えれば,もう少し効率よく座標が求められます。

ここはベクトルを用いると便利です。
$\overrightarrow{\text{P}_0\text{P}_2}=\overrightarrow{\text{OP}_2}-\overrightarrow{\text{OP}_0}$
$=(-2,2)-(2,0)$
$=(-4,2)$
これを反時計回りに 90° 回転させたベクトルは $(-2,-4)$ です。


$(-4,2)$ を 90° ずつ回転させてみると上のようになります。ようするに,$x$ と $y$ を入れ替えて,$x$ の符号を逆にしてやれば,反時計回りに 90° 回転したベクトルになるということです。
また,$n$ が 1 つ増えることに辺の長さは $\cfrac{\sqrt{2}}{2}$ 倍になるので,$n$ が 2 つ増えたときは $\Big(\cfrac{\sqrt{2}}{2}\Big)^2=\cfrac{1}{2}$ 倍になります。
よって
$\overrightarrow{\text{P}_2\text{P}_4}=\cfrac{1}{2}(-2,-4)=(-1,-2)$
同様にして
$\overrightarrow{\text{P}_4\text{P}_6}=\cfrac{1}{2}(2,-1)=\Big(1,-\cfrac{1}{2}\Big)$
$\overrightarrow{\text{P}_6\text{P}_8}=\cfrac{1}{2}\Big(\cfrac{1}{2},1\Big)=\Big(\cfrac{1}{4},\cfrac{1}{2}\Big)$
したがって
$\overrightarrow{\text{OP}_4}=\overrightarrow{\text{OP}}_2+\overrightarrow{\text{P}_2\text{P}_4}$
$=(-2,2)+(-1,-2)$
$=(-3,0)$
$\overrightarrow{\text{OP}_8}=\overrightarrow{\text{OP}}_4+\overrightarrow{\text{P}_4\text{P}_6}+\overrightarrow{\text{P}_6\text{P}_8}$
$=(-3,0)+\Big(1,-\cfrac{1}{2}\Big)+\Big(\cfrac{1}{4},\cfrac{1}{2}\Big)$
$=\Big(-\cfrac{7}{4},0\Big)$
$\text{P}_4(-3,0),\text{P}_8\Big(-\cfrac{7}{4},0\Big)$ (答え)
数列の和を求める
(3) 正の整数 $m$ に対して,$\text{P}_{8m}$ の座標を $m$ の式で表せ。
$\text{P}_0(2,0),\text{P}_8\Big(-\cfrac{7}{4},0\Big)$
から
$\overrightarrow{\text{P}_0\text{P}_8}=\overrightarrow{\text{OP}}_8-\overrightarrow{\text{OP}}_0$
$=\Big(-\cfrac{7}{4},0\Big)-(2,0)$
$=\Big(-\cfrac{15}{4},0\Big)$
となります。
もし $\overrightarrow{\text{P}_8\text{P}_{16}}$ を求めたいなら(2)でやった計算を繰り返していくことになるので
$\overrightarrow{\text{P}_8\text{P}_{16}}=\Big(\cfrac{1}{2}\Big)^4\cdot\overrightarrow{\text{P}_0\text{P}_8}$
$=\cfrac{1}{16}\cdot\Big(-\cfrac{15}{4},0\Big)$
という式になります。P は $\text{P}_0$ から $\text{P}_8$ を直線でつないでいくとうずまき型の形になるのですが,次の $\text{P}_8$ から $\text{P}_{16}$ はそれを $\cfrac{1}{16}$ に縮小した形になるわけです。
$\text{P}_{8m}$ の $y$ 座標はいずれも 0 となるので,$x$ 座標について考えていきましょう。
$\text{P}_{8m}$ の $x$ 座標を $x_{8m}$ とすると
$x_{8}=2-\cfrac{15}{4}$
$x_{16}=2-\cfrac{15}{4}-\cfrac{15}{4}\cdot\cfrac{1}{16}$
$x_{24}=2-\cfrac{15}{4}-\cfrac{15}{4}\cdot\cfrac{1}{16}-\cfrac{15}{4}\cdot\Big(\cfrac{1}{16}\Big)^2$
$x_{8m}=2-\cfrac{15}{4}-\cfrac{15}{4}\cdot\cfrac{1}{16}-\cfrac{15}{4}\cdot\Big(\cfrac{1}{16}\Big)^2-\cdots-\cfrac{15}{4}\Big(\cfrac{1}{16}\Big)^{m-1}$
$=2-\cfrac{15}{4}\Big\{1+\cfrac{1}{16}+\Big(\cfrac{1}{16}\Big)^2+\cdots+\Big(\cfrac{1}{16}\Big)^{m-1}\Big\}$
$\{\cdots\}$ の部分は初項 1,公比 $\cfrac{1}{16}$ の等比数列の和として考えることができます。
$2-\cfrac{15}{4}\cdot\cfrac{1-\Big(\cfrac{1}{16}\Big)^m}{1-\cfrac{1}{16}}$


$=2-\cfrac{15}{4}\cdot\cfrac{1-\Big(\cfrac{1}{16}\Big)^m}{\cfrac{15}{16}}$
$=2-\cfrac{15}{4}\cdot\cfrac{16}{15}\Big\{1-\Big(\cfrac{1}{16}\Big)^m\Big\}$
$=2-4\Big\{1-\Big(\cfrac{1}{16}\Big)^m\Big\}$
$=2-4+4\Big(\cfrac{1}{16}\Big)^m$
$=4\Big(\cfrac{1}{16}\Big)^m-2$
したがって
$\text{P}_{8m}\Big(4\Big(\cfrac{1}{16}\Big)^m-2,0\Big)$ (答え)
SNSでシェア