【数II】3 次関数と直線の共有点が 2 個になるとき（千葉大2020第2問）

公開日:2021/12/30

最終更新日:2023/01/11

$k$ を定数とし，$f(x)=x^3-kx$ とおく。曲線 $C:y=f(x)$ 上に原点と異なる点 $\text{P}(a,f(a))$ をとる。点 P を通り曲線 $C$ とちょうど 2 点を共有する 2 つの直線のうち，傾きが大きい方を $\ell_1$，小さい方を $\ell_2$ とする。さらに，$C$ と $\ell_1$ の共有点のうち P と異なるものを $\text{Q}_1$，$C$ と $\ell_2$ の共有点のうち P と異なるものを $\text{Q}_2$ とする。$\ell_1$ および $\ell_2$ の方程式と，$\text{Q}_1$ および $\text{Q}_2$ の座標を求めよ。

接線を求める

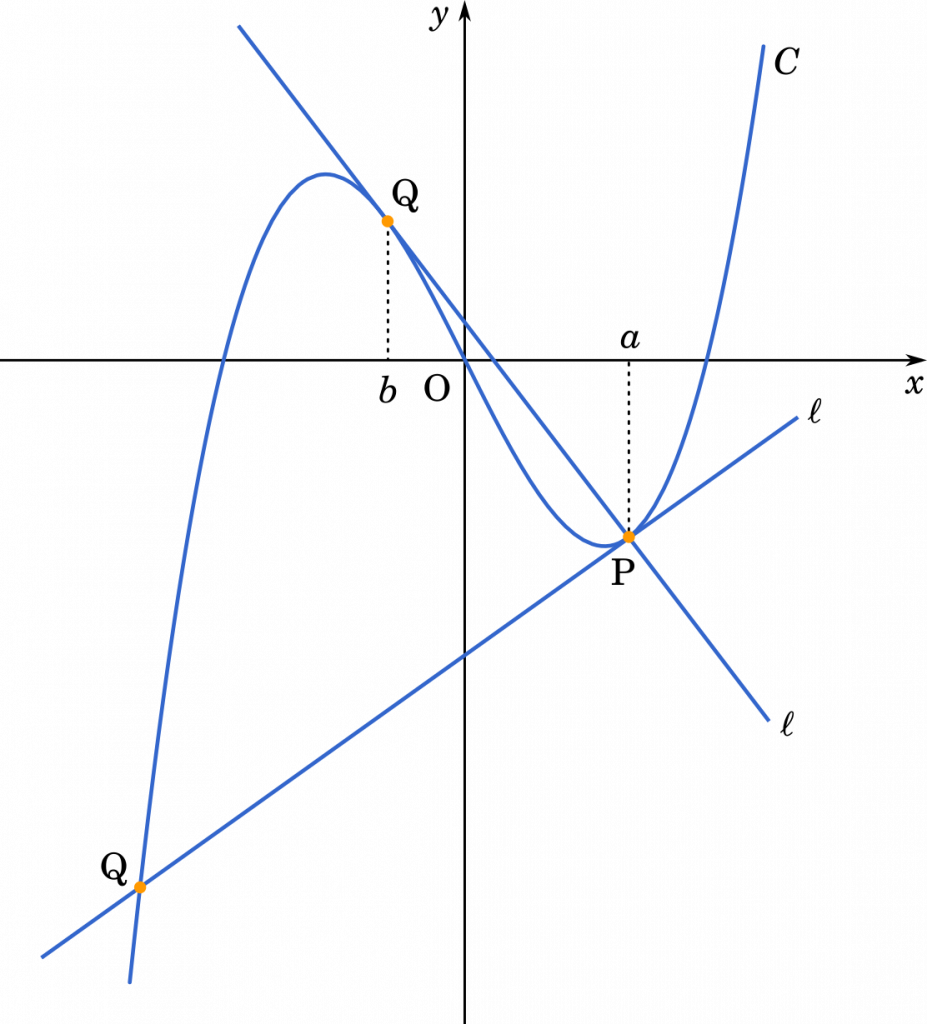
グラフを描いてみると分かりますが，直線のうち 1 つは $x=a$ における接線です。ただし，これが $\ell_1$ なのか $\ell_2$ なのかはわからないので，あとで決めたいと思います。

微分して
$f(x)=x^3-kx$
$f'(x)=3x^2-k$

$x=a$ における接線の傾きは

$f'(a)=3a^2-k$

これが，$(a,a^3-ka)$ を通るので，接線の式は

直線の方程式

点$(x_1,y_1)$を通り，傾きが $m$ の直線の方程式は
$y-y_1=m(x-x_1)$ つまり $y=m(x-x_1)+y_1$

$y=(3a^2-k)(x-a)+a^3-ka$

式を整理していきましょう。

$=(3a^2-k)x-(3a^2-k)a+a^3-ka$
$=(3a^2-k)x-3a^3+ka+a^3+ka$
$=(3a^2-k)x-2a^3$ ・・・①

これで直線の方程式が 1 つできました。

接点の x 座標を b とおく

もう一つの直線がうまく求められないです。

少しコツいるよね。

こういう場合，点 P を基準にして直線の式をつくろうとするとうまくいきません。

もう 1 の直線をよく見てみると，点 Q における接線になっていることが分かります。

そこで，点 Q の座標を $(b,f(b))$ として直線の式を作ってみましょう。

$x=b$ における接線の傾きは

$f'(b)=3b^2-k$

これが $(b,b^3-kb)$ を通るので，直線の式は

$y=(3b^2-k)(x-b)+b^3-kb$
$=(3b^2-k)x-2b^3$ ・・・②

これが $(a,a^3-ka)$ を通るので，代入すると

$a^3-ka=(3b^2-k)a-2b^3$
$a^3-ka=3ab^2-ka-2b^3$
$2b^3-3ab^2+a^3=0$

これを $b$ についての方程式とみなし，方程式を解いて $b$ を求めます。この方程式は $b=a$ とすると左辺が 0 になります。つまり式は $b-a$ で割り切れます。

組立除法を用いて因数分解しましょう。

$\begin{matrix}2&-3a&0&a^3|\underline{a}\\&2a&-2a^2&-a^3\\\hline2&-a&-a^2&0\end{matrix}$

$(b-a)(2b^2-ab-a^2)=0$

さらに $2b^2-ab-a^2$ は $b=a$ とすると 0 になるので，やはり $b-a$ で割り切れます。

$\begin{matrix}2&-a&-a^2|\underline{a}\\&2a&a^2\\\hline2&a&0\end{matrix}$

$(b-a)^2(2b+a)=0$

$2b+a=0$ とすると
$b=-\cfrac{a}{2}$

方程式の解は $b=a,-\cfrac{a}{2}$ となりますが，$b=a$ は点 P のことなので，$b=-\cfrac{a}{2}$ を点 Q の $x$ 座標としましょう。

これを②に代入して

$y=(3b^2-k)x-2b^3$
$=\Big\{3\cdot\Big(-\cfrac{a}{2}\Big)^2-k\Big\}x-2\Big(-\cfrac{a}{2}\Big)^3$
$=\Big(\cfrac{3}{4}a^2-k\Big)x+\cfrac{a^3}{4}$ ・・・③

直線の決定

$y=(3a^2-k)x-2a^3$ ・・・①
$y=\Big(\cfrac{3}{4}a^2-k\Big)x+\cfrac{a^3}{4}$ ・・・③

2 つの直線の式ができあがったので，傾きを比べて $\ell_1$ と $\ell_2$ を決めましょう。

$a$ がどんな値でも $a^2$ は正の数です。ということは

$3a^2>\cfrac{3}{4}a^2$
$3a^2-k>\cfrac{3}{4}a^2-k$

が成り立ちます。よって，①の式が $\ell_1$，③の式が $\ell_2$ です。

$\ell_1:y=(3a^2-k)x-2a^3$
$\ell_2:y=\Big(\cfrac{3}{4}a^2-k\Big)x+\cfrac{a^3}{4}$
（答え）

共有点の座標を求める

あとは $\text{Q}_1$ と $\text{Q}_2$ の座標を求めましょう。

まずは $\text{Q}_1$ から。

$\text{Q}_1$ は $\ell_1$ と $C$ の交点だから，式を連立して

$x^3-kx=(3a^2-k)x-2a^3$
$x^3-kx-(3a^2-k)x+2a^3=0$
$x^3-kx-3a^2x+kx+2a^3=0$
$x^3-3a^2x+2a^3=0$

式を因数分解します。

ここも $x=a$ とすると左辺が 0 になるし，そもそも共有点の 1 つは $x=a$ なんだから，解の 1 つは $x=a$ であるとも考えられるよね。

$\begin{matrix}1&0&-3a^2&2a^3&|\underline{a}\\&a&a^2&-2a^3\\\hline1&a&-2a^2&0\end{matrix}$

$(x-a)(x^2+ax-2a^2)=0$

$x^2+ax-2a^2=0$ とすると，同様に $x-a$ で割り切れるので

$\begin{matrix}1&a&-2a^2&|\underline{a}\\&a&2a^2\\\hline1&2a&0\end{matrix}$

$(x-a)^2(x+2a)=0$

よって $x=a,-2a$

$x=a$ は点 P のことなので，$\text{Q}_1$ の $x$ 座標は $-2a$ です。これを $y=x^3-kx$ に代入して

$y=(-2a)^3-k(-2a)$
$=-8a^3+2ka$

したがって

$\text{Q}_1(-2a,-8a^3+2ka)$ （答え）

さらに $\text{Q}_2$ の座標を求めましょう。

$\text{Q}_2$ の $x$ 座標は上でいったん求めていて，$x=-\cfrac{a}{2}$ でした。これを $y=x^3-kx$ に代入して

$y=\Big(-\cfrac{a}{2}\Big)^3-k\Big(-\cfrac{a}{2}\Big)$
$=-\cfrac{a^3}{8}+\cfrac{ka}{2}$