【数IA・IIB整数・数列】xn^3+yn^2が整数になるときの条件を考える（千葉大2021第4問）

公開日:2021/12/21

最終更新日:2023/01/11

$m$ を正の整数とする。座標平面上の点 $(x,y)$ で

$xn^3+yn^2$ $(n=1,2,3,\cdots)$

がすべて整数であるようなものは，連立不等式

$x\geqq0,y\geqq0,x+y\leqq m$

の表す領域に何個あるか答えよ。

x+y が整数になる場合

何から手をつけて良いのやら。

この問題では，示された条件がどういうときに成り立つのかを検討していきます。

もし，$n=1$ だとしたら，$xn^3+yn^2$ は

$x+y$

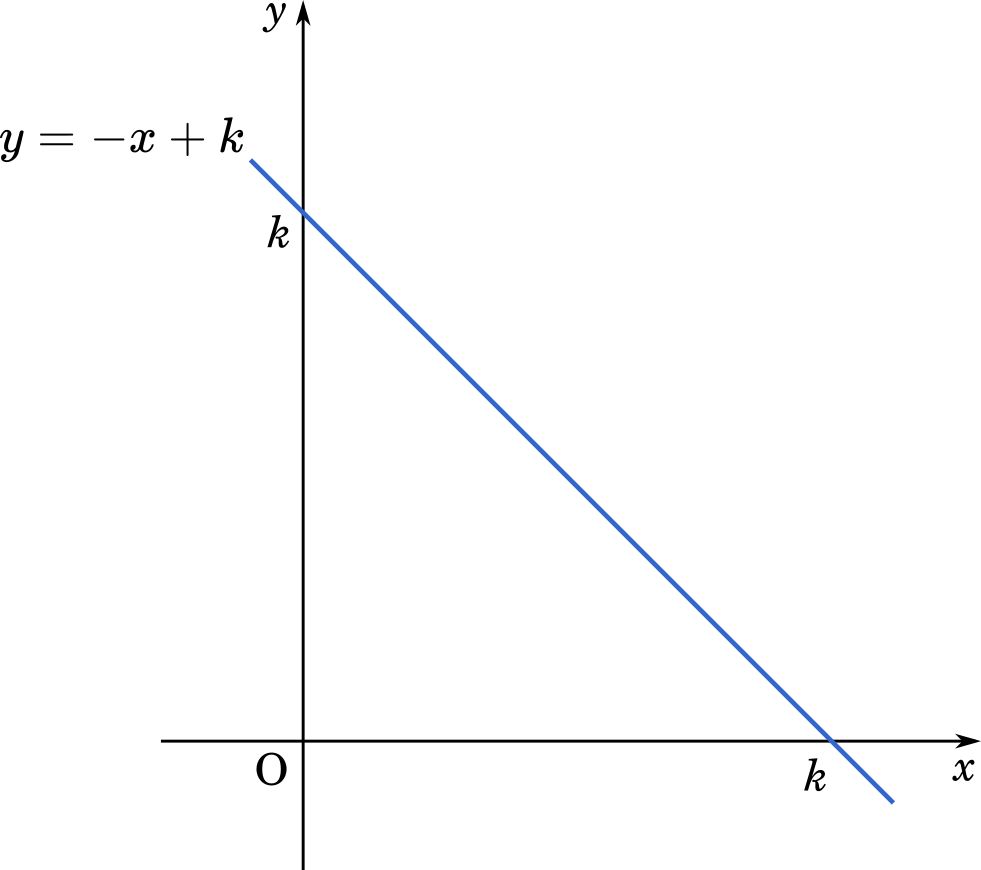
となります。これが整数になるので，$k$ を整数として

$k=x+y$
$y=-x+k$

となります。

このとき，$y=-x+k$ 上の点であれば，$x$ が何であろうが，$x+y$ は $k$ という整数になります。$x$ が実数であれば有理数でも無理数でも何でもオッケーです。

ここで確認したいのは，$x$ が何らかの値であるとき，それに対応する $y$ が必ず存在するということです。

つまり，何個ある？って言われたら，無限にあるってことになる。

無理数だと成り立たない

しかし問題文の条件は，すべての自然数 $n$ で整数になるというものです。

次に，$n=2$ として

$8x+4y$

とすると，$x$ は何でも良いとはいかなくなります。

まず，$x$ が無理数だと成り立ちません。

たとえば，前にもどって $n=1$ のとき，$x=\sqrt{2},k=3$ とすると

$y=-\sqrt{2}+3$

となります。$(x,y)=(\sqrt{2},3-\sqrt{2})$ は $x+y=3$ となるので，$x+y$ が整数になるパターンです。

次に，$8x+4y$ に $(x,y)=(\sqrt{2},3-\sqrt{2})$ を代入すると

$8\sqrt{2}+4(3-\sqrt{2})=4\sqrt{2}+12$

となるので，整数になりません。

これは $\sqrt{2}$ だけでなく無理数全体に当てはまる話です。$x+y$ において $x$ を無理数とすると，$y$ も無理数となり，$n=2$ としたときに無理数が消去できなくなるので，$8x+4y$ は整数になりません。

問題文の条件はすべての自然数 $n$ において整数にならならいといけないので，ここでアウトということになります。

なら虚数はダメ？

座標平面が出てきたらそもそも虚数は考えない。グラフ上に$(x,y)=(2i,3i)$ の点をおけって言われてもおけないでしょ？虚数ってのはあくまでグラフの外にあるどこか想像上の世界。グラフが出てきたら実数で考えるようにして。

x は有理数

となると，$x$ は有理数です。有理数は

$\cfrac{b}{a}$ ($b$ は整数，$a$ は 0 でない整数)

という形で表すことができます。

忘れてた人は数Iの教科書に戻って復習。

$x$ は $x=\cfrac{b}{a}$ という形で表せるとして，もう少し条件を絞ることはできないでしょうか。

もとの式を変形してみます。

$xn^3+yn^2$
$=n^2(xn+y)$
$=n^2\{x(n-1)+x+y\}$
$=xn^2(n-1)+n^2(x+y)$

上で述べた通り，何らかの有理数 $x$ が存在するとき，$x+y$ が整数になる $y$ は必ず存在します。

そこで，$n=1$ のとき $x+y$ は整数であるとして，$n=2$ 以降を検討しています。

$xn^2(n-1)+n^2(x+y)$

まず，$n$ が自然数であるため，$n^2(x+y)$ は整数です。

その上で $xn^2(n-1)$ も整数であれば，式全体が整数であると言えます。

$xn^2(n-1)$
$=x\cdot n\cdot n(n-1)$

式を分解して考えましょう。

$n(n-1)$ は偶数と奇数のかけ算として考えられます。たとえば，$n=3$ なら $n(n-1)=3\cdot2$ で，$n=4$ なら $n(n-1)=4\cdot3$ です。どちらかが偶数ならもう一つは奇数になります。

このとき，偶数×奇数＝偶数です。$n$ が偶数であっても奇数であっても，$n(n-1)$ は偶数になります。

それに $n$ をかけます。$n$ が偶数のとき，$n\cdot n(n-1)$ は偶数×偶数＝偶数となります。また，$n$ が奇数のとき，奇数×偶数＝偶数です。

結果として，$n^2(n-1)$ は偶数であることが分かります。

よって，$x$ が $\cfrac{\textsf{整数}}{2}$ の形であれば，$xn^2(n-1)$ はつねに整数になるはずです。

これをもう少し掘り下げましょう。

(i) $n$ が偶数のとき，$n=2t$ として

$xn^2(n-1)$
$=x(2t)^2(2t-1)$
$=x\cdot4t^2(2t-1)$

$n^2(n-1)$ は 4 の倍数となるので，$\cfrac{\textsf{整数}}{4}$ としても，$xn^2(n-1)$ は整数になります。

(ii) $n$ が奇数のとき，$n=2t+1$ として

$xn^2(n-1)$
$=x\cdot(2t+1)^2(2t+1-1)$
$=x\cdot(2t+1)^2\cdot2t$

$2t+1$ は奇数だから，$(2t+1)^2$ は奇数×奇数＝奇数となり，2 で割り切れません。つまり，$x$ を $\cfrac{\textsf{整数}}{4}$ とすると，$t$ の値によって $xn^2(n-1)$ は整数になったりならなかったりします。しかし，$x$ を $\cfrac{\textsf{整数}}{2}$ とすれば整数になると言えます。

(i),(ii) より $s$ を整数として，$x=\cfrac{s}{2}$ のとき，すべての自然数 $n$ において $xn^3+yn^2$ は整数となる。

これでようやく点を絞り込むことができました，$x$ は何でもよいわけではなく，$x=\cfrac{1}{2},\cfrac{2}{2},\cfrac{3}{2},\cdots$ のときにだけ，$xn^3+yn^2$ が整数となります。

点の数を数える

問題文の $x\geqq0,y\geqq0,x+y\leqq m$ にもとづいてグラフ上に点をおいていくと，次のようなグラフになります。

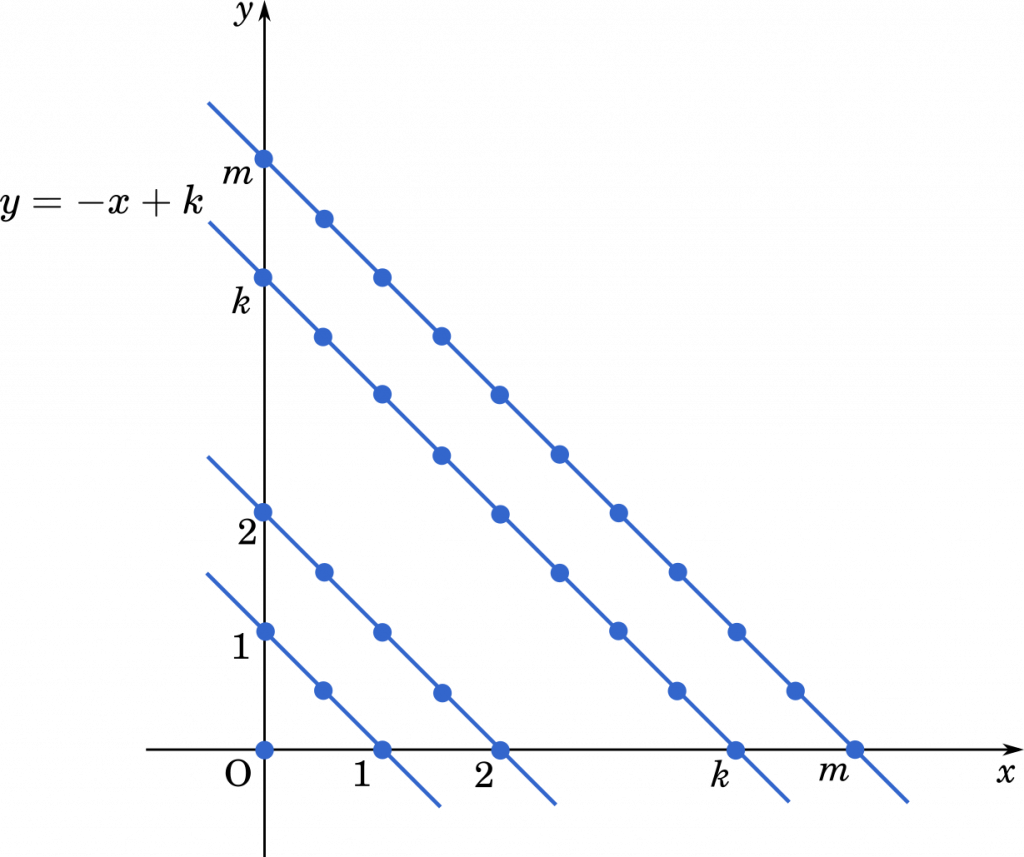
$x$ が $\cfrac{s}{2}$ の形のときに $x+y$ は整数となり，$xn^3+yn^2$ も整数となります。

たとえば，グラフ上の点 $\Big(\cfrac{1}{2},\cfrac{1}{2}\Big)$ で言えば，$x+y=\cfrac{1}{2}+\cfrac{1}{2}=1$ で整数となります。そして $\cfrac{1}{2}n^2+\cfrac{1}{2}n^2$ も整数となるわけです。

また，$(x,y)=(0,0)$ のときも，$xn^3+yn^2$ は整数（つまり 0 ）になるので，数え忘れないようにしましょう。

グラフ上の点の数を数えると

$x+y=1$ のときは 3 個。

$x+y=2$ のときは 5 個。

$x+y=k$ のときは $2k+1$ 個。