【数I 2つの円】3 つの円がそれぞれ接するときの半径を考える(千葉大2021第2問)

平面上に半径がそれぞれ $a^2,b^2,c^2$ $(0,a<b<c)$ の 3 つの円 $A,B,C$ および直線 $\ell$ がある。3 つの円はどれも直線 $\ell$ に接していて，どの 2 つの円も外接しているとする。

2 つの円が接するときの中心どうしの距離を利用する

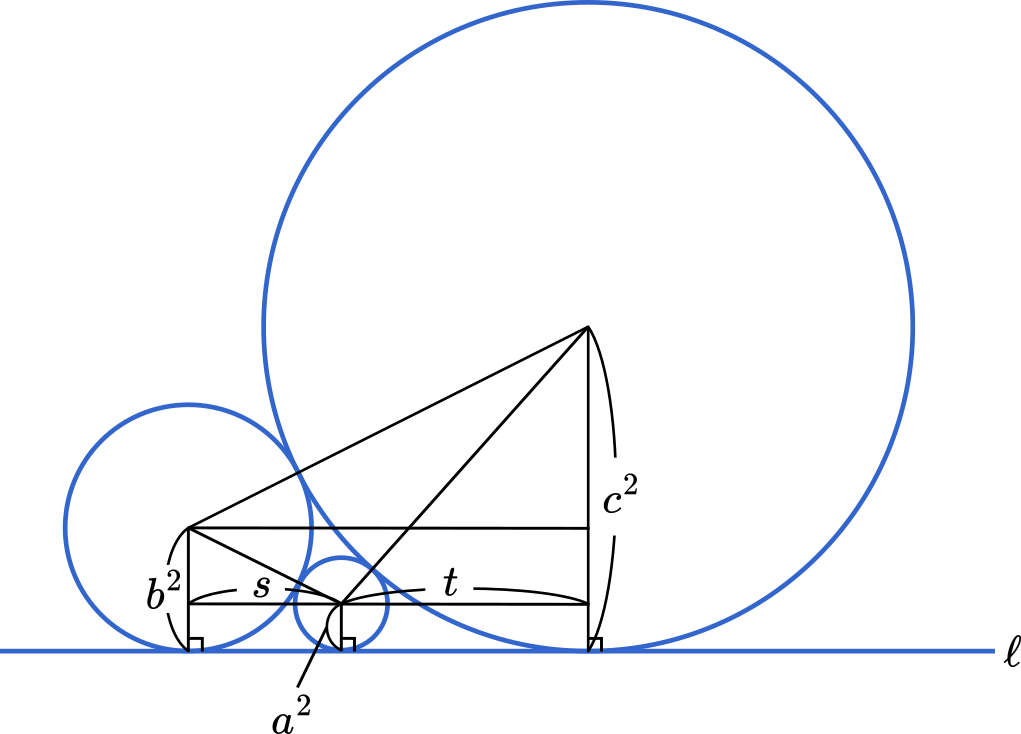
円の位置関係は上のようになります。ここから三平方の定理を用いて式をつくります。

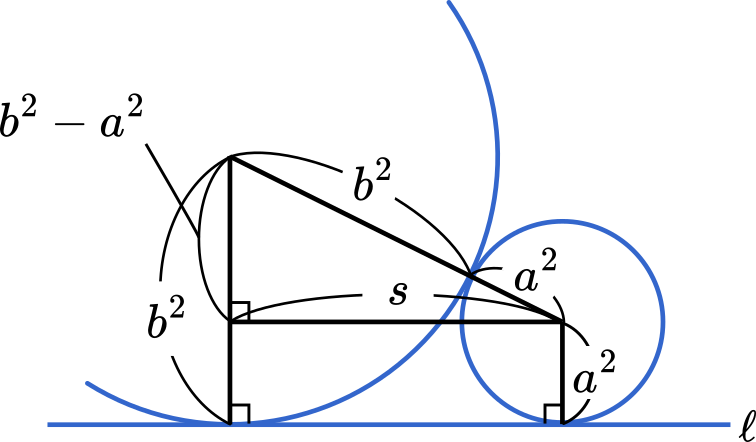
2 円の接する問題では，このように円の中心どうしを結んだ線を斜辺として直角三角形をつくるのがコツです。

$s^2+(b^2-a^2)^2=(a^2+b^2)^2$ ・・・①

同様に円 A，C について

$t^2+(c^2-a^2)^2=(a^2+c^2)^2$ ・・・②

さらに円 B，C について

$(s+t)^2+(c^2-b^2)^2=(b^2+c^2)^2$ ・・・③

これら 3 つの式から $s,t$ を消去していきます。

①より

$s^2=(a^2+b^2)^2-(b^2-a^2)^2$

ここは因数分解の公式 $a^2-b^2=(a+b)(a-b)$ を用いたほうが良いでしょう。

$=(a^2+b^2+b^2-a^2)(a^2+b^2-b^2+a^2)$
$=2b^2\cdot2a^2=4a^2b^2$
$s=2ab$

②より
$t^2=(a^2+c^2)^2-(c^2-a^2)^2$
$=(a^2+c^2+c^2-a^2)(a^2+c^2-c^2+a^2)$
$=2c^2\cdot2a^2=4a^2c^2$
$t=2ac$

③に代入して

$(2ab+2ac)^2+(c^2-b^2)^2=(b^2+c^2)^2$
$(2ab+2ac)^2=(b^2+c^2)^2-(c^2-b^2)^2$
$=(b^2+c^2+c^2-b^2)(b^2+c^2-c^2+b^2)$
$=2c^2\cdot2b^2=4b^2c^2$
$2ab+2ac=2bc$
$ab+ac=bc$
$bc-ac=ab$
$c(b-a)=ab$
$c=\cfrac{ab}{b-a}$　（答え）

等比数列の公比を求める

$a,b,c$ が等比数列となるとき，その公比を $r$ とすると

$a=\cfrac{b}{r}$，$c=br$

が成り立ちます。

よって(1)で求めた式は

$ab+ac=bc$
$\cfrac{b}{r}\cdot b+\cfrac{b}{r}\cdot br=b\cdot br$

両辺を $b^2$ で割ると

$\cfrac{1}{r}+1=r$
$1+r=r^2$
$r^2-r-1=0$
$r=\cfrac{1\pm\sqrt{5}}{2}$

$a<b<c$ より $r>0$ だから

$r=\cfrac{1+\sqrt{5}}{2}$　（答え）