長方形が回転してできる円の面積（千葉大2021第1問）

定数 aa は 16<a<14\cfrac{1}{6}<a<\cfrac{1}{4} を満たすとする。座標平面上の長方形 ABCD は以下の 4 つの条件を満たす。

・2 点 A，B は放物線 y=−x2+2ay=-x^2+2a 上にある。
・2 点 C，D は放物線 y=2x2−ay=2x^2-a 上にある。
・2 点 A，D の xx 座標は等しく，かつ正である。
・点 A の yy 座標は点 D の yy 座標より大きい。

点 A の xx 座標を tt とする。長方形 ABCD の周および内部を，原点を中心に 1 回転させてできる図形の面積を SS とする。

(1) SS を tt の式で表せ。

(2) SS の最大値と，そのときの tt の値を求めよ。

長方形を 1 回転させてできる図形の面積

(1) SS を tt の式で表せ。

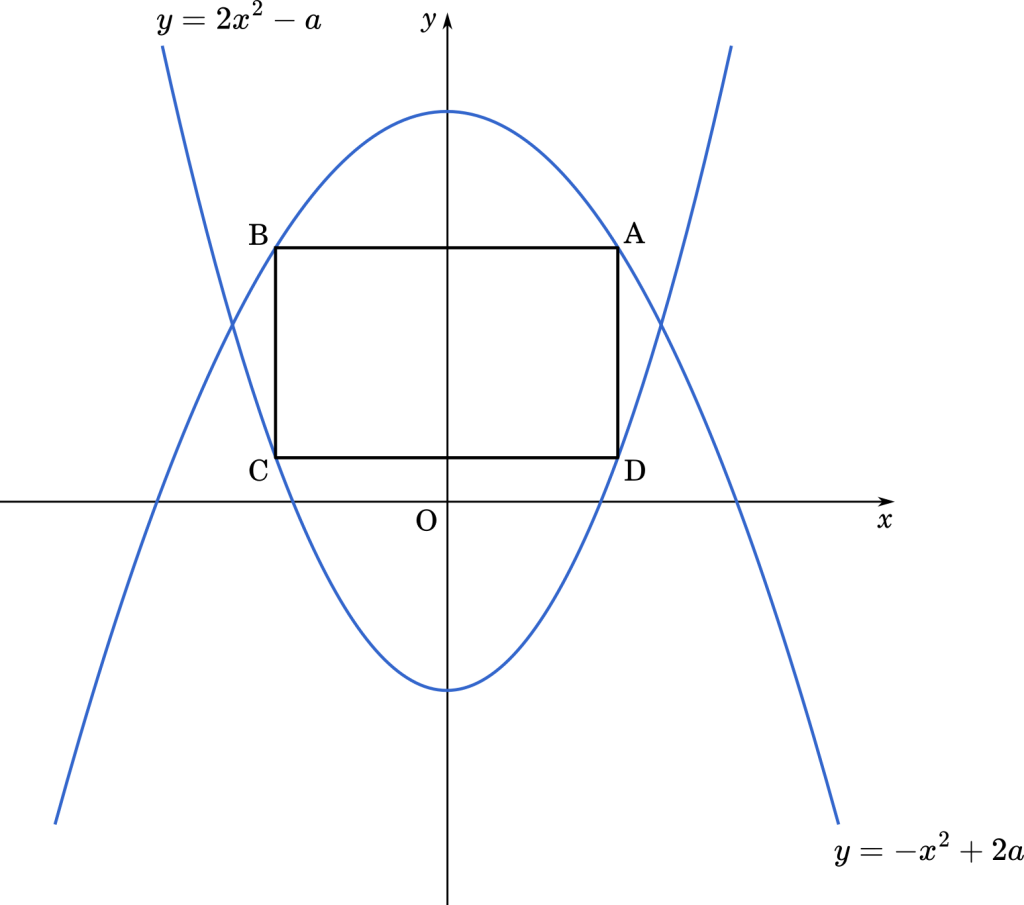
問題文の条件をもとに図を描くと上のようになります。今回のポイントは点 D が xx 軸より上にあるか下にあるかでもとめる図形の形が異なるところです。

点 D が xx 軸より上にあるとき

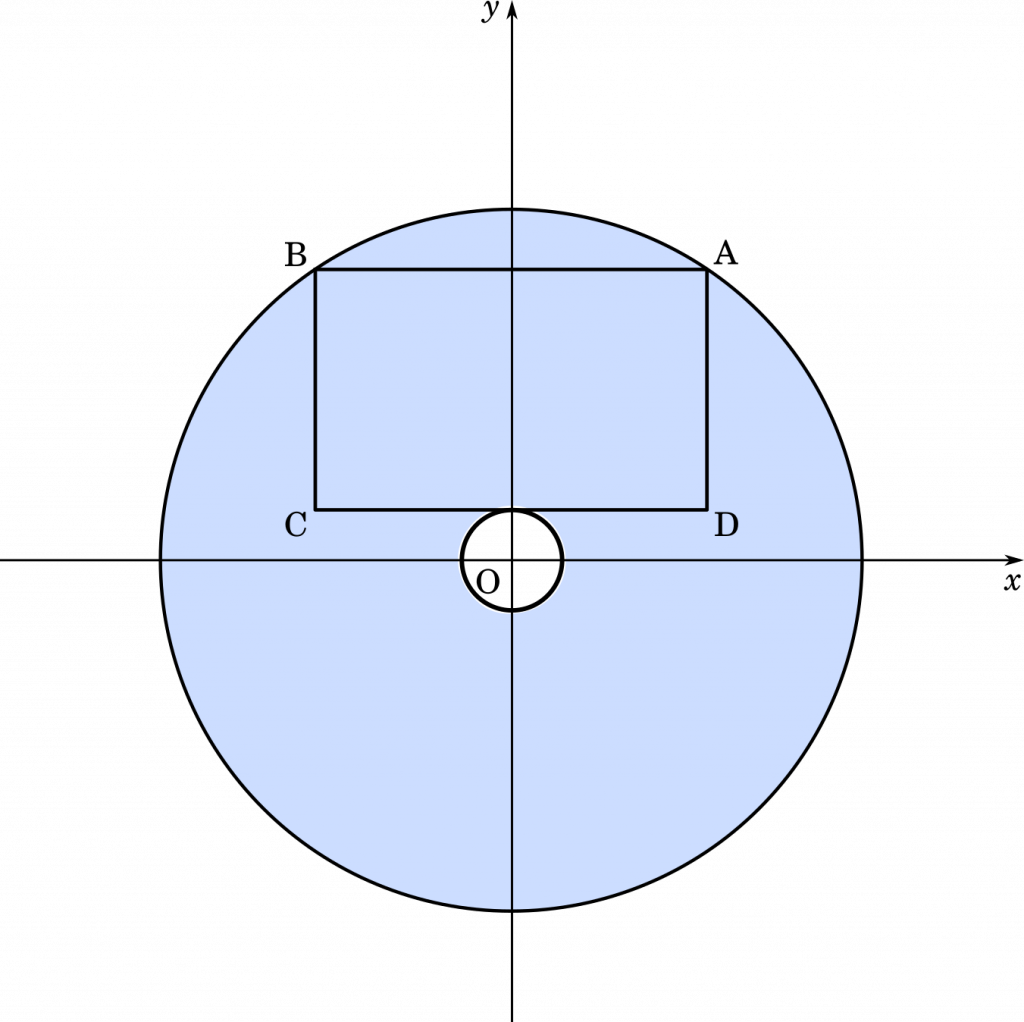
このように，大きな円から小さな円の面積を引いたものが SS になります。大きな円の半径は OA で，小さな円の半径は点D の yy 座標となります。

点 D が xx 軸より下にあるとき

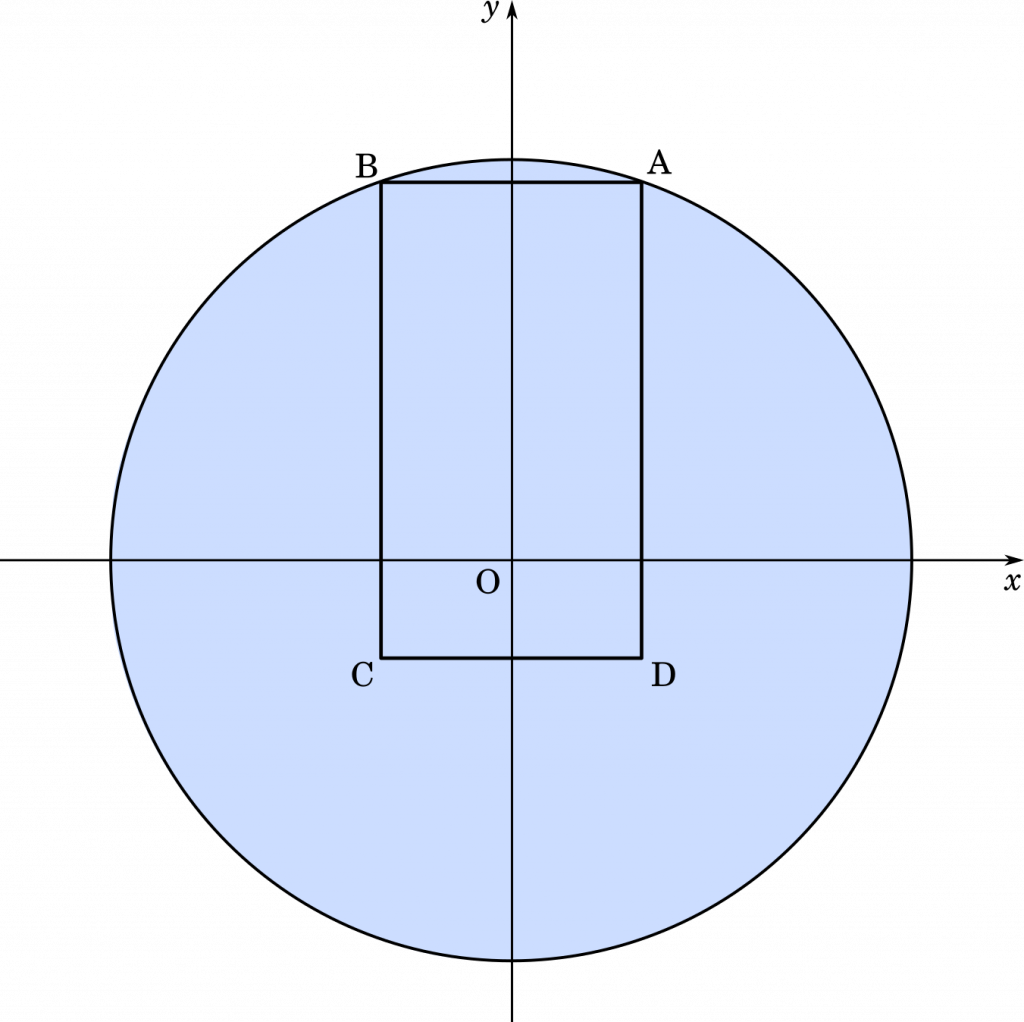
今度は OA を半径とする円の面積を求めれば良いことになります。

まず，ABCD の座標を求めましょう。

A(t,−t2+2a)(t,-t^2+2a)
B(−t,−t2+2a)(-t,-t^2+2a)
C(−t,2t2−a)(-t,2t^2-a)
D(t,2t2−a)(t,2t^2-a)

また，2 点 A，D の xx 座標は等しく，かつ正である，という条件から

t>0t>0 ・・・①

が成り立ちます。

さらに，点 A の yy 座標は点 D の yy 座標より大きい，という条件から

−t2+2a>2t2−a-t^2+2a>2t^2-a
3t2<3a3t^2<3a
t2<at^2<a
−a<t<a-\sqrt{a}<t<\sqrt{a} ・・・②

①，②より

0<t<a0<t<\sqrt{a}

問題文の条件を式として表すのがポイント。

次に円の半径を求めましょう。

OA2=t2+(−t2+2a)2\text{OA}^2=t^2+(-t^2+2a)^2
=t2+t4−4at2+4a2=t^2+t^4-4at^2+4a^2
=t4+(1−4a)t2+4a2=t^4+(1-4a)t2+4a^2 ・・・③
OD2=t2+(2t2−a)2\text{OD}^2=t^2+(2t^2-a)^2
=t2+4t4−4at2+a2=t^2+4t^4-4at^2+a^2
=4t4+(1−4a)t2+a2=4t^4+(1-4a)t^2+a^2 ・・・④

ここから，点 D が xx 軸より上にあるとき，つまり大きな円から小さな円の面積を引くパターンを考えてみましょう。

(i) 2t2−a≧02t^2-a\geqq0 のとき

2t2≧a2t^2\geqq a
t2≧a2t^2\geqq\cfrac{a}{2}

t>0t>0 より

t≧a2t\geqq\sqrt{\cfrac{a}{2}}

このとき

S=πOA2−πOD2S=\pi\text{OA}^2-\pi\text{OD}^2
=π{t4+(1−4a)t2+4a2}−π(2t2−a)2=\pi\{t^4+(1-4a)t^2+4a^2\}-\pi(2t^2-a)^2
=π{t4+(1−4a)t2+4a2−4t2+4at2−a2}=\pi\{t^4+(1-4a)t^2+4a^2-4t^2+4at^2-a^2\}
=π(−3t4+t2+3a2)=\pi(-3t^4+t^2+3a^2)

次に，点 D が xx 軸より下にあるときを求めます。

(ii) 2t2−a<02t^2-a<0 のとき

2t2<a2t^2<a
t2<a2t^2<\cfrac{a}{2}

t>0t>0 より

t<a2t<\sqrt{\cfrac{a}{2}}

このとき

S=πOA2S=\pi\text{OA}^2
=π{t4+(1−4a)t2+4a2}=\pi\{t^4+(1-4a)t^2+4a^2\}

したがって

S=π(−3t4+t2+3a2)S=\pi(-3t^4+t^2+3a^2) (a2≦t<a)\Big(\sqrt{\cfrac{a}{2}}\leqq t<\sqrt{a}\Big)

S=π{t4+(1−4a)t2+4a2}S=\pi\{t^4+(1-4a)t^2+4a^2\} (0<t<a2)\Big(0<t<\sqrt{\cfrac{a}{2}}\Big)

(答え)

最大値を求める

(2) SS の最大値と，そのときの tt の値を求めよ。

(1)で求めた通り，SS は 2 パターンあるので，それぞれについて最大値を求め，それらのうち大きな方を SS 最大値とします。

(i) a2≦t<a\sqrt{\cfrac{a}{2}}\leqq t<\sqrt{a} のとき

S=π(−3t4+t2+3a2)S=\pi(-3t^4+t^2+3a^2)

ここで −3t4+t2+3a2-3t^4+t^2+3a^2 について

t2=kt^2=k として

−3k2+k+3a2-3k^2+k+3a^2

平方完成すると

=−3(k2−k3)+3a2=-3\Big(k^2-\cfrac{k}{3}\Big)+3a^2
=−3(k−16)2+112+3a2=-3\Big(k-\cfrac{1}{6}\Big)^2+\cfrac{1}{12}+3a^2

よって最大値は π(112+3a2)\pi\Big(\cfrac{1}{12}+3a^2\Big)

(ii) 0<t<a20<t<\sqrt{\cfrac{a}{2}} のとき

S=π{t4+(1−4a)t2+4a2}S=\pi\{t^4+(1-4a)t^2+4a^2\}

t4+(1−4a)t2+4a2t^4+(1-4a)t^2+4a^2 について

t2=kt^2=k として

k2+(1−4a)k+4a2k^2+(1-4a)k+4a^2
=(k+1−4a2)2−(1−4a)24+4a2=\Big(k+\cfrac{1-4a}{2}\Big)^2-\cfrac{(1-4a)^2}{4}+4a^2
=(k+1−4a2)2−1−8a+16a2−16a24=\Big(k+\cfrac{1-4a}{2}\Big)^2-\cfrac{1-8a+16a^2-16a^2}{4}
=(k+1−4a2)2+8a−14=\Big(k+\cfrac{1-4a}{2}\Big)^2+\cfrac{8a-1}{4}
=(k+1−4a2)2+2a−14=\Big(k+\cfrac{1-4a}{2}\Big)^2+2a-\cfrac{1}{4}

今度は下に凸のグラフなので，頂点は最小値を表します。グラフの軸は −1−4a2-\cfrac{1-4a}{2} です。

−1−4a2=4a−12-\cfrac{1-4a}{2}=\cfrac{4a-1}{2}
=2a−12=2a-\cfrac{1}{2}

ここで 16<a<14\cfrac{1}{6}<a<\cfrac{1}{4} という条件を考えると，

a<14a<\cfrac{1}{4}
2a<122a<\cfrac{1}{2}
2a−12<02a-\cfrac{1}{2}<0

となるので，頂点は yy 軸より左側になります。一方で，tt は正の数だから 0<t<a20<t<\sqrt{\cfrac{a}{2}} の区間でグラフは単調増加です。

結局，最大値どうなるの？
2 つグラフをつなげるとこんな感じ。

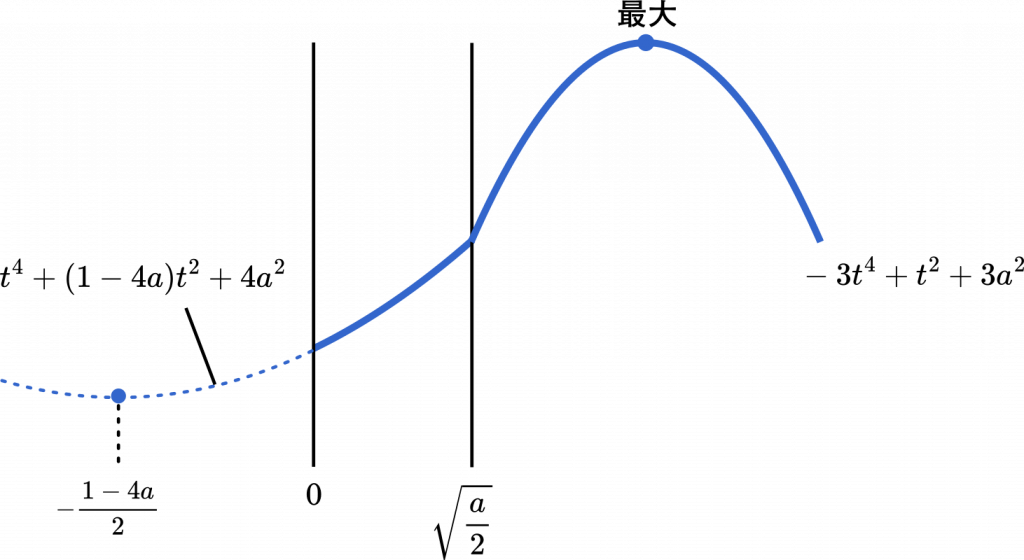
よって，π(112+3a2)\pi\Big(\cfrac{1}{12}+3a^2\Big) が最大値です。

最大値は k=16k=\sqrt{\cfrac{1}{6}} のとき π(112+3a2)\pi\Big(\cfrac{1}{12}+3a^2\Big)　（答え）

SNSでシェア

mm参考書 2019-2023