【数III微分積分】媒介変数を用いて道のりと速さを求める練習問題（神戸大2021理系第5問）

三平方の定理

距離は三平方の定理を用いて求めます。

$\text{OP}^2=\sqrt{x^2+y^2}$
$=\Big(\cfrac{4+5\cos t}{5+4\cos t}\Big)^2+\Big(\cfrac{3\sin t}{5+4\cos t}\Big)^2$
$=\cfrac{16+40\cos t+25\cos^2 t+9\sin^2 t}{(5+4\cos t)^2}$

ここで，三角比の公式より $\sin^2 t=1-\cos^2 t$ を用いるともう少し式が整理できます。

$=\cfrac{16+40\cos t+25\cos^2 t+9(1-\cos^2 t)}{(5+4\cos t)^2}$
$=\cfrac{16+40\cos t+25\cos^2 t+9-9\cos^2 t}{(5+4\cos t)^2}$
$=\cfrac{16\cos^2t+40\cos t+25}{(5+4\cos t)^2}$

分子の式は因数分解できます。

$=\cfrac{(4\cos t+5)^2}{(5+4\cos t)^2}$
$=1$　（答え）

速度を求める

変位 $x$ を微分すると横軸方向の速度を求めることができます。さらに，速度を微分したら加速度が求められます。

物理で習う公式 $x=v_ot+\cfrac{1}{2}at^2$ も同じです。

$v_ot+\cfrac{1}{2}at^2$

$t$ で微分すると

$v_o+at$　（速度）

さらに微分すると

$a$　（加速度）

逆の関係も成り立ちます。加速度を積分すれば速度になり，速度を積分すれば距離（変位）になります。この関係は(3)で用います。

速度を求めていきましょう。

$\cfrac{dx}{dt}=\cfrac{(4+5\cos t)'(5+4\cos t)-(4+5\cos t)(5+4\cos t)’}{(5+4\cos t)^2}$
$=\cfrac{-5\sin t(5+4\cos t)+(4+5\cos t)\cdot4\sin t}{(5+4\cos t)^2}$
$=\cfrac{-25\sin t-20\sin t\cos t+16\sin t+20\sin t\cos t}{(5+4\cos t)^2}$
$=\cfrac{-9\sin t}{(5+4\cos t)^2}$

また

$\cfrac{dy}{dt}=\cfrac{(3\sin t)'(5+4\cos t)-3\sin t(5+4\cos t)’}{(5+4\cos t)^2}$
$=\cfrac{3\cos t(5+4\cos t)-3\sin t(-4\sin t)}{(5+4\cos t)^2}$
$=\cfrac{15\cos t+12\cos^2t+12\sin^2t}{(5+4\cos t)^2}$
$=\cfrac{15\cos t+12\cos^2t+12(1-\cos^2t)}{(5+4\cos t)^2}$
$=\cfrac{15\cos t+12\cos^2t+12-12\cos^2t}{(5+4\cos t)^2}$
$=\cfrac{15\cos t+12}{(5+4\cos t)^2}$

したがって

$\vec{v}=\Bigg(\cfrac{-9\sin t}{(5+4\cos t)^2},\cfrac{15\cos t+12}{(5+4\cos t)^2}\Bigg)$

速さ $|\vec{v}|$ は三平方の定理で求めます。

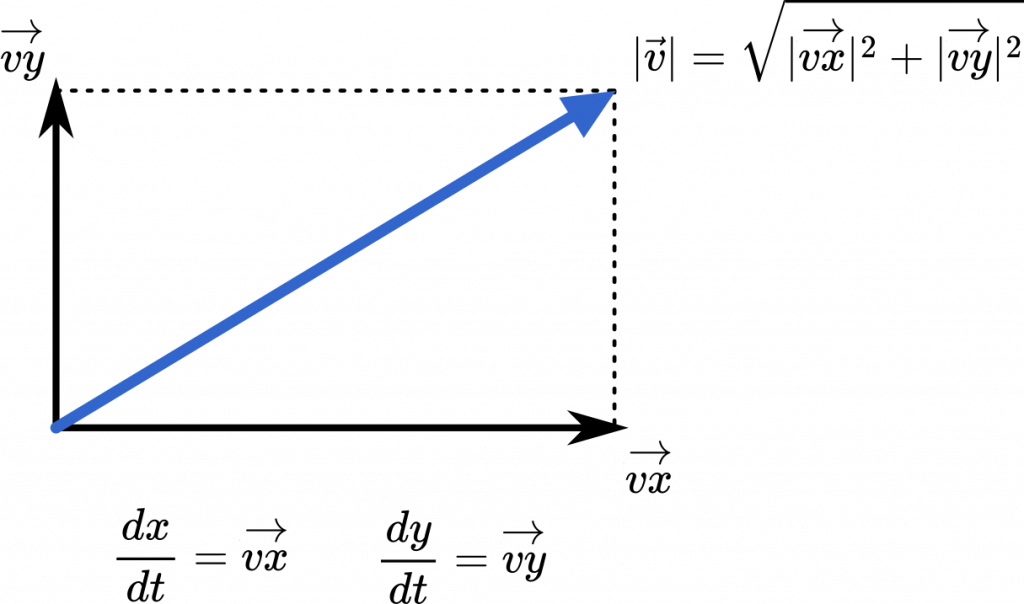
$|\vec{v}|^2=\Big(\cfrac{-9\sin t}{(5+4\cos t)^2}\Big)^2+\Big(\cfrac{15\cos t+12}{(5+4\cos t)^2}\Big)^2$
$=\cfrac{(-9\sin t)^2+(15\cos t+12)^2}{(5+4\cos t)^4}$
$=\cfrac{81\sin^2t+225\cos^2t+360\cos t+144}{(5+4\cos t)^4}$
$=\cfrac{81(1-\cos^2t)+225\cos^2t+360\cos t+144}{(5+4\cos t)^4}$
$=\cfrac{81-81\cos^2t+225\cos^2t+360\cos t+144}{(5+4\cos t)^4}$
$=\cfrac{144\cos^2+360\cos t+225}{(5+4\cos t)^4}$

分子を因数分解します。

$=\cfrac{(12\cos t+15)^2}{(5+4\cos t)^4}$

よって

$|\vec{v}|=\cfrac{12\cos t+15}{(5+4\cos t)^2}$
$=\cfrac{3(4\cos t+5)}{(5+4\cos t)^2}$
$=\cfrac{3}{5+4\cos t}$　（答え）

速度と距離の関係

ここは(2)の結果を利用しましょう。

$\displaystyle\int_0^\pi\cfrac{dt}{5+4\cos t}$
$\displaystyle=\cfrac{1}{3}\int_0^\pi\cfrac{3}{5+4\cos t}\space dt$
$\displaystyle=\cfrac{1}{3}\int_0^\pi|\vec{v}|\space dt$

ここで定積分が半円になることを示しておきましょう。

$\cfrac{dx}{dt}=\cfrac{-9\sin t}{(5+4\cos t)^2}$ より

$0\leqq t\leqq\pi$ において

$\cfrac{dx}{dt}\leqq0$

また

$\cfrac{dy}{dt}=\cfrac{15\cos t+12}{(5+4\cos t)^2}$ より

$15\cos t+12=0$ とすると
$5\cos t+4=0$
$\cos t=-\cfrac{4}{5}$

ここから $\sin t$ を求めると

$\sin t=\sqrt{1-\Big(-\cfrac{4}{5}\Big)^2}$
$=\sqrt{1-\cfrac{16}{25}}$
$=\sqrt{\cfrac{9}{25}}$

$0\leqq t\leqq\pi$ より

$=\cfrac{3}{5}$

増減表は

$\def\arraystretch{1.5}\begin{array}{|c||c|c|c|c|c|}\hline t&0&\cdots&\alpha&\cdots&\pi\\\hline\frac{dx}{dt}&0&-&&-&0\\\hline x&1&\searrow&0&\searrow&-1\\\hline\frac{dy}{dt}&\frac{1}{3}&+&0&-&-3\\\hline y&0&\nearrow&1&\searrow&0\\\hline\end{array}$

$t=\alpha$ のとき

$x=\cfrac{4+5\Big(-\cfrac{4}{5}\Big)}{5+4\Big(-\cfrac{4}{5}\Big)}$
$=\cfrac{20-20}{25-16}=0$
$y=\cfrac{3\cdot\cfrac{3}{5}}{5+4\Big(-\cfrac{4}{5}\Big)}$
$=\cfrac{9}{25-16}$
$=1$

$\text{OP}=1$ より，$\displaystyle\int_0^\pi|\vec{v}|\space dt$ は半円の周の長さである。

したがって

$\displaystyle=\cfrac{1}{3}\int_0^\pi|\vec{v}|\space dt$

$=\cfrac{\pi}{3}$　（答え）