【数II3次式の因数分解】4次方程式の解が重複する場合を考える(神戸大2021理系第4問)
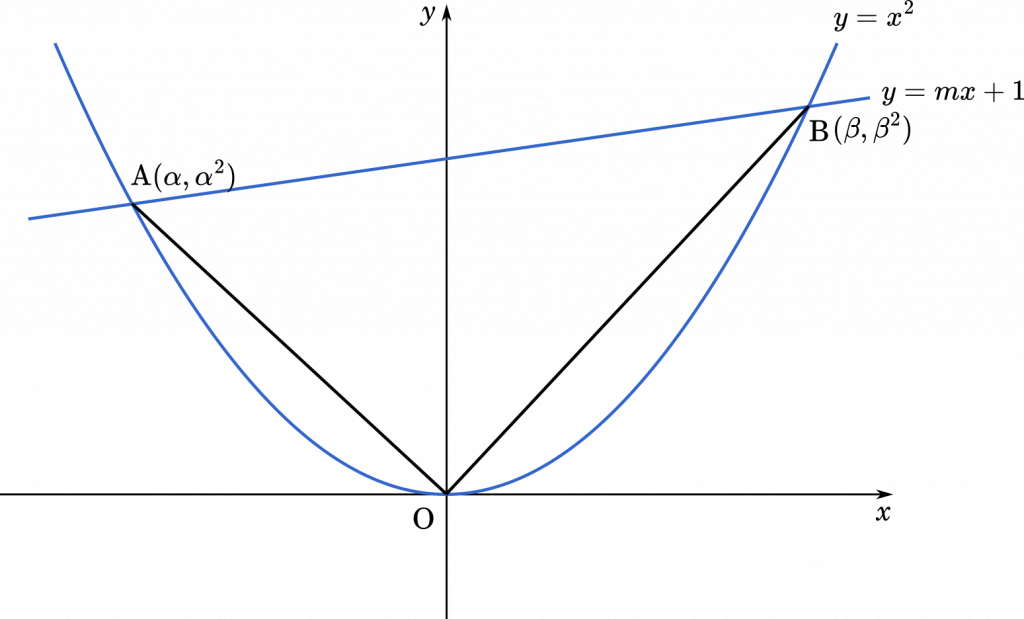
(1) $\angle\text{AOB}=\cfrac{\pi}{2}$ が成り立つことを示せ。
(2) 3 点 A,B,O を通る円の方程式を求めよ。
(3) 放物線 $y=x^2$ と(2)の円が A,B,O 以外の共有点をもたないような $m$ の値をすべて求めよ。
解と係数の関係
(1) $\angle\text{AOB}=\cfrac{\pi}{2}$ が成り立つことを示せ。
共有点を求めます。
$y=x^2$ と $y=mx+1$ を連立して
$x^2=mx+1$
$x^2-mx-1=0$ ・・・①
ここで,解と係数の関係を使います。
2 次方程式 $ax^2+bx+c=0$ の 2 つの解を $\alpha,\beta$ とすると
$\alpha+\beta=-\cfrac{b}{a}$,$\alpha\beta=\cfrac{c}{a}$
ここで共有点の座標を $\text{A}(\alpha,\alpha^2)$,$\text{B}(\beta,\beta^2)$ とすると,①の解は $\alpha$ と $\beta$ になります。
解と係数の関係より
$\alpha+\beta=m$ ・・・②
$\alpha\beta=-1$ ・・・③
直線 AO の傾きは
$\cfrac{\alpha^2}{\alpha}=\alpha$
直線 OB の傾きは
$\cfrac{\beta^2}{\beta}=\beta$
となるので,③より
$\angle\text{AOB}=\cfrac{\pi}{2}$ (証明終わり)

円の方程式
(2) 3 点 A,B,O を通る円の方程式を求めよ。

中学で習った円周角の定理を思い出しましょう。
$\angle\text{AOB}$ が 90° なら AB は直径を表します。
よって,円の中心を P とすると,点 P は辺 AB の中点です。また,半径は辺 OP となります。
中心の座標と半径が分かれば円の方程式が作れます。
AB の中点を P とすると,②より
$\cfrac{\alpha+\beta}{2}=\cfrac{m}{2}$
ここも解と係数の関係を利用しています。
これを $y=mx+1$ に代入すると
$y=m\cdot\cfrac{m}{2}+1$
$=\cfrac{m^2}{2}+1$
よって,点 P の座標は
$\text{P}\Big(\cfrac{m}{2},\cfrac{m^2}{2}+1\Big)$
次に半径を求めます。三平方の定理を用いて
$\text{OP}^2=\Big(\cfrac{m}{2}\Big)^2+\Big(\cfrac{m^2}{2}+1\Big)^2$
$=\cfrac{m^2}{4}+\cfrac{m^4}{4}+m^2+1$
$=\cfrac{m^4}{4}+\cfrac{5}{4}m^2+1$
円の方程式
点$(a,b)$ を中心とする半径 $r$ の円の方程式は
$(x-a)^2+(y-b)^2=r^2$
円の方程式は
$\Big(x-\cfrac{m}{2}\Big)^2+\Big(y-\cfrac{m^2}{2}-1\Big)^2=\cfrac{m^4}{4}+\cfrac{5}{4}m^2+1$
式を整理していきます。$\Big(y-\cfrac{m^2}{2}-1\Big)^2$ の部分は公式を使いましょう。
公式 $(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca$
$x^2-mx+\cfrac{m^2}{4}+y^2+\cfrac{m^4}{4}+1-m^2y+m^2-2y=\cfrac{m^4}{4}+\cfrac{5}{4}m^2+1$
$x^2+y^2-mx-(m^2+2)y=0$ (答え)
因数分解
(3) 放物線 $y=x^2$ と(2)の円が A,B,O 以外の共有点をもたないような $m$ の値をすべて求めよ。
共有点を求めるので,(2)で求めた円の方程式と $y=x^2$ を連立します。
$x^2+y^2-mx-(m^2+2)y=0$ に $y=x^2$ を代入すると
$x^2+x^4-mx-(m^2+2)x^2=0$
$x^4-(m^2+1)x^2-mx=0$
このようにして,$x$ の式とします。

$x\{x^3-(m^2+1)x-m\}=0$
$x^3-(m^2+1)x-m$ をさらに因数分解します。

そこで,$x=-m$ とすると
$-m^3+(m^2+1)m-m=0$
このとき,式は $x+m$ で割り切れます。組立除法を用いましょう。
$\begin{matrix}1&0&-m^2-1&-m&|\underline{-m}\\&-m&m^2&m\\\hline1&-m&-1&0\end{matrix}$
よって
$x(x+m)(x^2-mx-1)=0$ ・・・④
この式は 4 次方程式なので 4 つの解を持ちます。一方,問題文の条件で A,B,O 以外の共有点をもたないとあるので,解は 3 つにしなければなりません。


④の解は $x=0,-m$ または $x^2-mx-1=0$ の解です。$x^2-mx-1=0$ は基本的に 2 つの解をとるので 4 つの解が存在することになるのですが,$m$ の値によって解が 3 つになる場合があります。解が重複するケースを検討してみましょう。
たとえば $m=0$ とすると,④は
$x^2(x^2-1)=0$
$x^2(x+1)(x-1)=0$
となるので,解は $x=0,1,-1$ となり 3 の解を持ちます。
また別のパターンとして $x^2-mx-1$ が重解を持つときも,④の解は 3 つだけになるはずです。
$x^2-mx-1=0$ が重解を持つとき,判別式を用いて
$D=m^2+4=0$
$m^2=-4$


あともう一つ考えられるパターンは $x^2-mx-1=0$ の解の一つが $-m$ になる場合です。
$x=-m$ とすると
$m^2+m^2-1=0$
$2m^2-1=0$
$m^2=\cfrac{1}{2}$
$m=\pm\cfrac{1}{\sqrt{2}}$
したがって
$m=0,\pm\cfrac{1}{\sqrt{2}}$ (答え)
SNSでシェア