【数IIB数列】2 次関数の最大・最小がつくる数列／特性方程式で一般項を求める(神戸大2020文系第2問)

数学的帰納法

まず $n=1$ として，初項を代入してみます。

$f_1(x)=a_1(x+1)^2+2b_1$
$=(x+1)^2+2$

この 2 次関数は下に凸で頂点が $(-1,2)$ です。

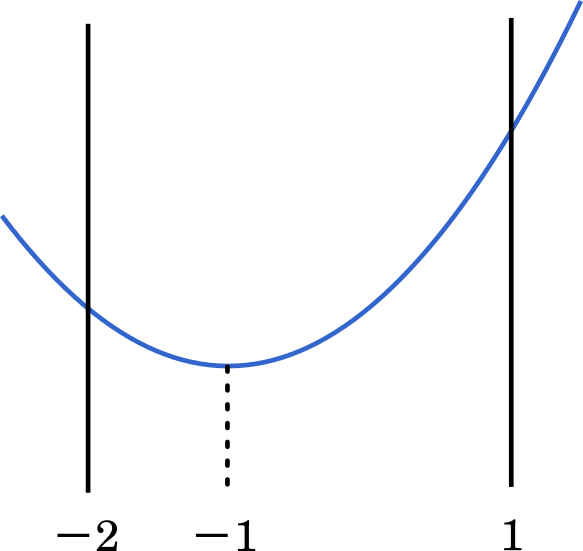
$-2\leqq x\leqq1$ の範囲では，最大は $x=1$ のときで，最小は $x=-1$ のときで，最小値 2 です。

$f_1(1)=(1+1)^2+2=6$

よって

$a_2=6,b_2=2$

同じことを繰り返していきます。

$f_2(x)=a_2(x+1)^2+2b_2$
$=6(x+1)^2+4$

$a_3=28,b_3=4$

$a_n>0$，$b_n>0$ はちゃんと成り立つようです。

これがすべての自然数 $n$ について成り立つことを示すには，数学的帰納法を用いるとよいでしょう。

すべての自然数 $n$ について

$a_n>0,b_n>0$ ・・・（＊）

[I] $n=1$ のとき

$a_1=b_1=1$

よって，$n=1$ のとき（＊）が成り立つ。

[II] $n=k$ のとき（＊）が成り立つと仮定すると

$f_k(x)=a_k(x+1)^2+2b_k$

$a_k>0$ より，$f_k(x)$ は下に凸のグラフで，$x=1$ のとき最大値をとり，また最小値は $2b_k$ となるので

$a_{k+1}=f_k(1)$
$4a_k+2b_k>0$
$b_{k+1}=2b_k>0$

よって，$n=k$ のとき（＊）が成り立つ。
[I],[II]より，すべての自然数 $n$ において，（＊）が成り立つ。（証明終わり）

一般項を求める

(2) 数列 $\{b_n\}$ の一般項を求めよ。

(1)を振り返ると，$b_2=2b_1$，$b_3=2b_2$，・・・という関係になっていました。よって

$b_1=1$

$b_{n+1}=2b_n$

これは初項 1，公比 2 の等比数列です。

$b_n=2^{n-1}$　（答え）

さらに一般項を求める

(3) $c_n=\cfrac{a_n}{2^n}$ とおく。数列 $\{c_n\}$ の一般項を求めよ。

(1)，(2)を手がかりに，$a_n$ について考えてみましょう。

$a_n$ は $f_n(x)$ の最大値のほうで，$x=1$ のときに最大値をとりました。

$f_1(1)=a_1(1+1)^2+2b_1=a_2$
$f_2(1)=a_2(1+1)^2+2b_2=a_3$

となります。

ここから，漸化式が考えられます。

$a_{n+1}=4a_n+2b_n$

(2)より，$b_n=2^{n-1}$ だから

$a_{n+1}=4a_n+2\cdot2^{n-1}$
$=4a_n+2^n$

これをもとにすると，今度は $c_n$ の漸化式がつくれそうです。

$c_{n+1}=\cfrac{a_{n+1}}{2^{n+1}}$
$=\cfrac{4a_n+2^n}{2^{n+1}}$
$=\cfrac{4a_n}{2^{n+1}}+\cfrac{2^n}{2^{n+1}}$
$=\cfrac{2a_n}{2^n}+\cfrac{1}{2}$
$=2c_n+\cfrac{1}{2}$

漸化式ができあがりました。

$\alpha=2\alpha+\cfrac{1}{2}$ として
$\alpha=-\cfrac{1}{2}$

$\begin{matrix}&c_{n+1}&=&2c_n&+&\cfrac{1}{2}\\-)&\alpha&=&2\alpha&+&\cfrac{1}{2}\\\hline&c_{n+1}-\alpha&=&2(c_n-\alpha)\end{matrix}$

$\alpha=\cfrac{1}{2}$ を代入して

$c_{n+1}-\cfrac{1}{2}=2\Big(c_n-\cfrac{1}{2}\Big)$　・・・①

$c_n+\cfrac{1}{2}=d_n$ として

$d_1=c_1+\cfrac{1}{2}$
$=\cfrac{a_1}{2}+\cfrac{1}{2}$
$=1$

よって，①は

$d_{n+1}=2d_n$

となる。

これは，初項 1，公比 2 の等比数列だから，一般項は

$d_n=2^{n-1}$

$c_n+\cfrac{1}{2}=2^{n-1}$
$c_n=2^{n-1}-\cfrac{1}{2}$　（答え）