因数定理と組立除法を用いて形の分からない式がαで割り切れることを証明する(神戸大2020文系第1問)
$\alpha$ は実数とし,$f(x)$ は係数が実数である 3 次式で,次の条件 (i),(ii) をみたすとする。
(i) $f(x)$ の $x^3$ の係数は 1 である。
(ii) $f(x)$ とその導関数 $f'(x)$ について,
$$f(\alpha)=f(\alpha)=0$$
が成り立つ。
以下の問に答えよ。
(1) $f(x)$ は $(x-\alpha)^2$ で割り切れることを示せ。
(2) $f(\alpha+2)=0$ とする。$f'(x)=0$ かつ $x\not=\alpha$ をみたす $x$ を $\alpha$ を用いて表わせ。
(3) (2)の条件のもとで $\alpha=0$ とする。$xy$ 平面において不等式
$y\geqq f(x)$ かつ $y\geqq f'(x)$ かつ $y\leqq0$
の表す部分の面積を求めよ。
組立除法を利用する
(1) $f(x)$ は $(x-\alpha)^2$ で割り切れることを示せ。


まず,$f(x)=x^3+px^2+qx+r$ としてみましょう。
$f(x)=x^3+px^2+qx+r$ ・・・①
微分すると
$f'(x)=3x^2+2px+q$ ・・・②
それぞれに $x=\alpha$ を代入すると
$f(\alpha)=\alpha^3+p\alpha^2+q\alpha+r=0$ ・・・③
$f'(\alpha)=3\alpha^2+2p\alpha+q=0$ ・・・④


組立除法を用いて
$\begin{matrix}1&p&q&r&|\underline{\alpha}\\&\alpha&\alpha^2+p\alpha&\alpha^3+p\alpha^2+q\alpha\\\hline 1&\alpha+p&\alpha^2+p\alpha+q&\alpha^3+p\alpha^2+q\alpha+r\end{matrix}$
こうすると,$\alpha^3+p\alpha^2+q\alpha+r$ が割り算した余りになるのですが,③より 0 になります。

$f(x)=(x-\alpha)\{x^2+(\alpha+p)x+\alpha^2+p\alpha+q\}$
$x^2+(\alpha+p)x+\alpha^2+p\alpha+q$ さらに $x-\alpha$ で割ります。
$\begin{matrix}1&\alpha+p&\alpha^2+p\alpha+q&|\underline{\alpha}\\&\alpha&2\alpha^2+p\alpha\\\hline1&2\alpha+p&3\alpha^2+2p\alpha+q\end{matrix}$
$3\alpha^2+2p\alpha+q$ が割り算した余りですが,④より 0 になります。
したがって
$f(x)=(x-\alpha)^2(x+2\alpha+p)$ ・・・⑤
となるので,$f(x)$ は $(x-\alpha)^2$ で割り切れる。(証明終わり)
もう一つの解を求める
(2) $f(\alpha+2)=0$ とする。$f'(x)=0$ かつ $x\not=\alpha$ をみたす $x$ を $\alpha$ を用いて表わせ。
$f(\alpha+2)=0$ ということは,$f(x)$ は $x-\alpha-2$ で割り切れるということです。
ということは,(1)の結果も考えると,$f(x)$ は $(x-\alpha)^2$ かつ $x-\alpha-2$ で割り切れる,つまり
$f(x)=(x-\alpha)^2(x-\alpha-2)$ ・・・⑥
となります。これと⑤を比べると
$2\alpha+p=-\alpha-2$
$p=-3\alpha-2$
④に代入すると
$3\alpha^2+2(-3\alpha-2)\alpha+q=0$ $3\alpha^2-6\alpha^2-4\alpha+q=0$
$q=3\alpha^2+4\alpha$
$p,q$ の値を②に代入すると
$f'(x)=3x^2+2(-3\alpha-2)x+3\alpha^2+4\alpha=0$
$3x^2-2(3\alpha+2)x+3\alpha^2+4\alpha=0$ ・⑦
2 次方程式の解の公式を使って解を求めます。
$x=\cfrac{3\alpha+2\pm\sqrt{(3\alpha+2)^2-3(3\alpha^2+4\alpha)}}{3}$
$=\cfrac{3\alpha+2\pm2}{3}$
$=\alpha+\cfrac{4}{3},\alpha$
$x\not=\alpha$ より
$x=\alpha+\cfrac{4}{3}$ (答え)
増減表をつくってグラフの概形を考える
(3) (2)の条件のもとで $\alpha=0$ とする。$xy$ 平面において不等式
$y\geqq f(x)$ かつ $y\geqq f'(x)$ かつ $y\leqq0$
の表す部分の面積を求めよ。
面積を求めるには,$y=f(x)$ と $y=f'(x)$ のグラフを描いてみる必要があります。
そこで,微分して増減表をつくってみましょう。
⑥,⑦より
$f(x)=(x-\alpha)^2(x-\alpha-2)$
$f'(x)=3x^2-2(3\alpha+2)x+3\alpha^2+4\alpha$
だったので,$\alpha=0$ を代入すると
$f(x)=x^2(x-2)$ ・・・⑧
$f'(x)=3x^2-4x$ ・・・⑨
となります。
(2)より $f'(x)=0$ の解は $x=0,\cfrac{4}{3}$ だったので,増減表は
$\def\arraystretch{1.5}\begin{array}{|c||c|c|c|c|c|}\hline x&\cdots&0&\cdots&\frac{4}{3}&\cdots\\\hline f'(x)&+&0&-&0&+\\\hline f(x)&\nearrow&0&\searrow&-\frac{32}{27}&\nearrow\\\hline\end{array}$
$f(0)=0$
$f\Big(\cfrac{4}{3}\Big)=\Big(\cfrac{4}{3}\Big)^2\Big(\cfrac{4}{3}-2\Big)$
$=\cfrac{16}{9}\cdot\Big(-\cfrac{2}{3}\Big)=-\cfrac{32}{27}$
次に,$y=f'(x)$ のグラフを描くためにさらに微分しましょう。
$f”(x)=6x-4$
$6x-4=0$ とすると $x=\cfrac{2}{3}$
増減表は
$\def\arraystretch{1.5}\begin{array}{|c||c|c|c|}\hline x&\cdots&\frac{2}{3}&\cdots\\\hline f”(x)&-&0&+\\\hline f'(x)&\searrow&-\frac{4}{3}&\nearrow\\\hline\end{array}$
$f’\Big(\cfrac{2}{3}\Big)=3\Big(\cfrac{2}{3}\Big)^2-4\cdot\cfrac{2}{3}$
$=\cfrac{4}{3}-\cfrac{8}{3}=-\cfrac{4}{3}$
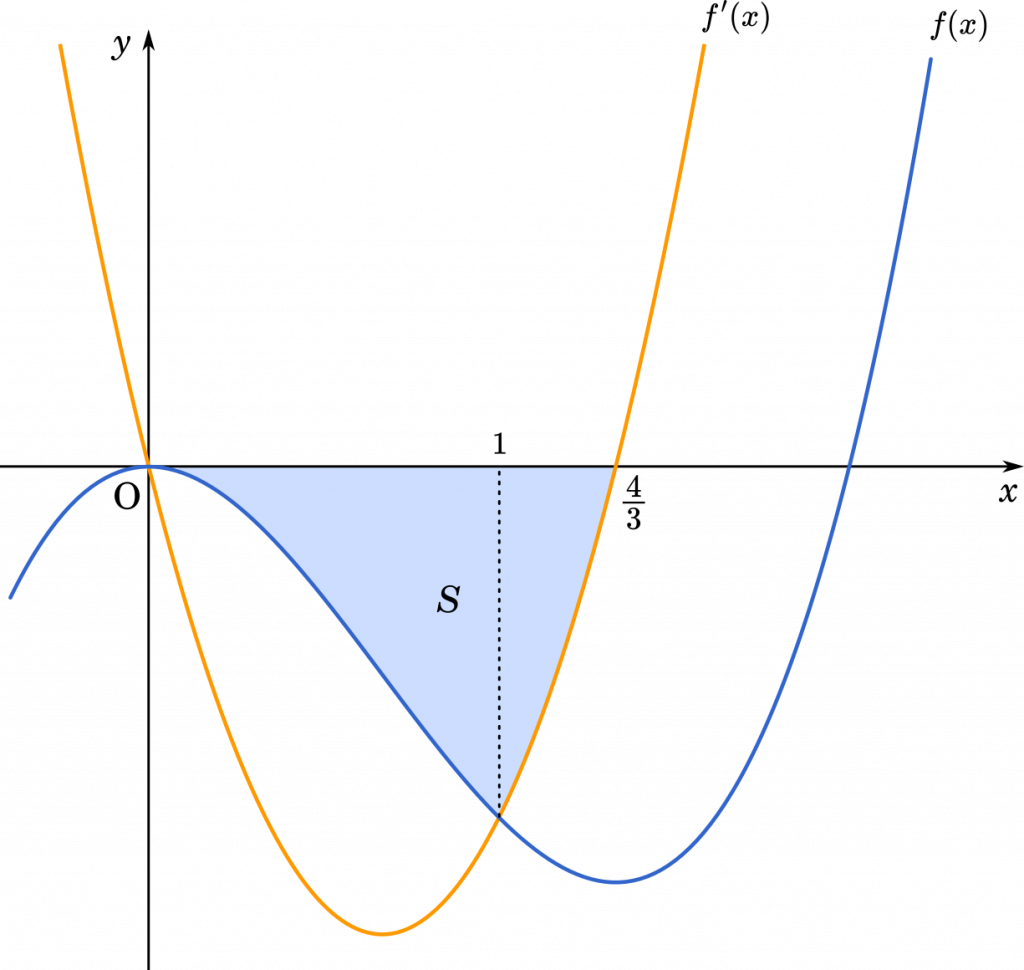
$f(x)$ と $f'(x)$ の交点を求めると
$x^3-2x^2=3x^2-4x$
$x^3-5x^2+4x=0$
$x(x^2-5x+4)=0$
$x(x-1)(x-4)=0$
よって,$f(x)$ と $f'(x)$ が交わるのは $x=0,1,4$ のとき。
グラフの概形ができあがったので,これをもとに面積を求めます。
$\displaystyle S=-\int_0^1f(x)\space dx-\int_1^{\small{\frac{4}{3}}}f'(x)\space dx$

$\displaystyle=-\int_0^1x^3-2x^2\space dx-\int_1^{\small{\frac{4}{3}}}3x^2-4x\space dx$
$=-\Big[\cfrac{x^4}{4}-\cfrac{2}{3}x^3\Big]_0^1-\Big[x^3-2x^2\Big]_1^{\small{\frac{4}{3}}}$
$=-\Big(\cfrac{1}{4}-\cfrac{2}{3}\Big)-\Big(\cfrac{64}{27}-\cfrac{32}{9}-1+2\Big)$
通分してまとめていきます。
$=-\cfrac{1}{4}+\cfrac{18}{27}-\cfrac{64}{27}+\cfrac{96}{27}-1$
$=-\cfrac{1}{4}+\cfrac{50}{27}-1$
$=\cfrac{-27+200}{108}-1$
$=\cfrac{173-108}{108}$
$=\cfrac{65}{108}$ (答え)
SNSでシェア